BackJoon Algorithm - Java

문제

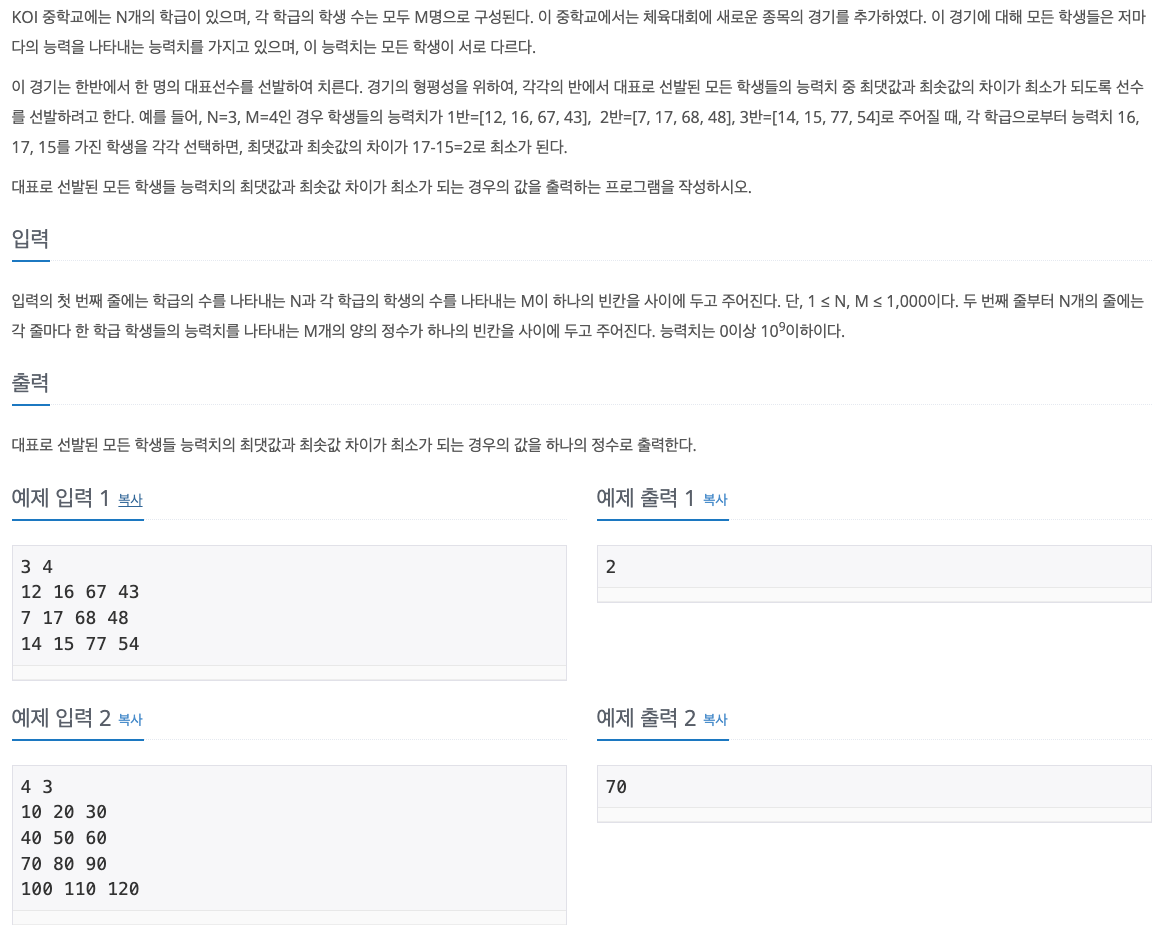
풀이

..

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class Back_2461 {
    public static void main(String[] args) throws IOException {
        // 입력을 받기 위한 BufferedReader 생성
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        // 첫 번째 줄에서 N과 M 값을 입력받음
        StringTokenizer token = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(token.nextToken());  // N: 클래스의 수
        int M = Integer.parseInt(token.nextToken());  // M: 각 클래스의 학생 수

        // 각 클래스마다 우선순위 큐로 학생들의 능력을 관리 (오름차순 정렬)
        List<PriorityQueue<Long>> classes = new LinkedList<>();
        for (int i = 0; i < N; i++) {
            token = new StringTokenizer(br.readLine());
            PriorityQueue<Long> pq = new PriorityQueue<>();
            for (int j = 0; j < M; j++) {
                pq.add(Long.parseLong(token.nextToken()));  // 각 학생의 능력치 입력
            }
            classes.add(pq);  // 해당 클래스의 학생 능력치를 우선순위 큐로 저장
        }

        // 결과 값을 저장할 변수 (최솟값을 찾기 위해 Long.MAX_VALUE로 초기화)
        long answer = Long.MAX_VALUE;

        // 현재까지 확인한 학생 능력치 중 가장 큰 값 저장
        long max_value = -1;

        // 각 클래스에서 가장 작은 학생 능력치를 담는 우선순위 큐 (오름차순 정렬)
        PriorityQueue<long[]> pg = new PriorityQueue<>((a, b) -> Long.compare(a[0], b[0]));

        // 각 클래스에서 가장 작은 능력치 학생을 pg 큐에 추가하고, 그 중 최대 값을 갱신
        for (int i = 0; i < N; i++) {
            long value = classes.get(i).remove();  // 각 클래스에서 가장 작은 능력치 학생을 추출
            pg.add(new long[] {value, i});  // 그 값과 해당 클래스 인덱스를 우선순위 큐에 추가
            if (value > max_value) {  // 최대값 갱신
                max_value = value;
            }
        }

        // 우선순위 큐를 이용하여 가능한 모든 최소 차이를 계산
        while (true) {
            long[] now = pg.remove();  // 가장 작은 능력치를 가진 학생을 추출

            // 현재 최소값과 최대값의 차이가 더 작다면 answer 갱신
            if (answer > Math.abs(now[0] - max_value)) {
                answer = Math.abs(now[0] - max_value);
            }

            // 해당 클래스에 더 이상 학생이 없다면 종료
            if (classes.get((int) now[1]).isEmpty()) {
                break;
            }

            // 해당 클래스에서 새로운 학생의 능력치를 가져옴
            long tmp = classes.get((int) now[1]).remove();

            // 새로 가져온 값이 현재까지의 최대값보다 크면 최대값을 갱신
            if (tmp > max_value) {
                max_value = tmp;
            }

            // 새로운 학생의 능력치를 우선순위 큐에 추가
            pg.add(new long[] {tmp, now[1]});
        }

        // 가장 작은 최대-최소 차이를 출력
        System.out.println(answer);
    }
}

1) 입력

3 4
12 16 67 43
7 17 68 48
14 15 77 54

2) 초기 상태

• N = 3: 3개의 클래스.
• M = 4: 각 클래스에 4명의 학생.

각 클래스의 학생 능력치는 다음과 같습니다

클래스 1: 12, 16, 67, 43
클래스 2: 7, 17, 68, 48
클래스 3: 14, 15, 77, 54

2-1) 각 클래스의 능력치를 오름차순 정렬

클래스 1: 12, 16, 43, 67
클래스 2: 7, 17, 48, 68
클래스 3: 14, 15, 54, 77

2-2) 각 클래스에서 가장 작은 값 추출 (첫 번째 단계)

• 각 클래스에서 가장 작은 값을 우선순위 큐에 삽입하면서 최대값(max_value)을 갱신합니다.

클래스 1에서 12 추출 → pg.add([12, 0])
클래스 2에서 7 추출 → pg.add([7, 1])
클래스 3에서 14 추출 → pg.add([14, 2])

• 현재 max_value = 14 (세 클래스 중 가장 큰 값)
• 우선순위 큐(pg) 상태: [(7, 1), (12, 0), (14, 2)]

2-3) 최소값과 최대값 차이 계산

• 현재 최소값은 7, 최대값은 14이므로, 차이는

  14 - 7

  = 7.

• answer = 7 (최초 갱신)

2-4) 클래스 2에서 새로운 값 추출

• 클래스 2에서 다음으로 작은 값 17을 추출 → pg.add([17, 1])
• 현재 max_value = 17으로 갱신 (새로 추출된 값이 최대값)
• 우선순위 큐(pg) 상태: [(12, 0), (14, 2), (17, 1)]

2-5) 최소값과 최대값 차이 계산:

• 현재 최소값은 12, 최대값은 17이므로, 차이는

  17 - 12

  = 5.

• answer = 5 (갱신)

2-6) 클래스 1에서 새로운 값 추출

• 클래스 1에서 다음으로 작은 값 16을 추출 → pg.add([16, 0])
• 현재 max_value = 17 유지 (새로 추출된 값이 최대값보다 작음)
• 우선순위 큐(pg) 상태: [(14, 2), (17, 1), (16, 0)]

2-7) 최소값과 최대값 차이 계산

• 현재 최소값은 14, 최대값은 17이므로, 차이는

  17 - 14

  = 3.

• answer = 3 (갱신)

2-8) 클래스 3에서 새로운 값 추출

• 클래스 3에서 다음으로 작은 값 15을 추출 → pg.add([15, 2])
• 현재 max_value = 17 유지 (새로 추출된 값이 최대값보다 작음)
• 우선순위 큐(pg) 상태: [(15, 2), (17, 1), (16, 0)]

2-9) 최소값과 최대값 차이 계산

• 현재 최소값은 15, 최대값은 17이므로, 차이는

  17 - 15

  = 2.

• answer = 2 (갱신)

2-10) 클래스 3에서 새로운 값 추출

• 클래스 3에서 다음으로 작은 값 54을 추출 → pg.add([54, 2])
• 현재 max_value = 54로 갱신 (새로 추출된 값이 최대값보다 큼)
• 우선순위 큐(pg) 상태: [(16, 0), (17, 1), (54, 2)]

2-11) 최소값과 최대값 차이 계산

• 현재 최소값은 16, 최대값은 54이므로, 차이는

  54 - 16

  = 38.

• answer = 2 (변경 없음)

2-12) 클래스 1에서 새로운 값 추출

• 클래스 1에서 다음으로 작은 값 43을 추출 → pg.add([43, 0])
• 현재 max_value = 54 유지 (새로 추출된 값이 최대값보다 작음)
• 우선순위 큐(pg) 상태: [(17, 1), (43, 0), (54, 2)]

2-13) 최소값과 최대값 차이 계산

• 현재 최소값은 17, 최대값은 54이므로, 차이는

  54 - 17

  = 37.

• answer = 2 (변경 없음)

2-14) 클래스 2에서 새로운 값 추출

• 클래스 2에서 다음으로 작은 값 48을 추출 → pg.add([48, 1])
• 현재 max_value = 54 유지
• 우선순위 큐(pg) 상태: [(43, 0), (48, 1), (54, 2)]

2-15) 최소값과 최대값 차이 계산

• 현재 최소값은 43, 최대값은 54이므로, 차이는

  54 - 43

  = 11.

• answer = 2 (변경 없음)

2-16) 클래스 1에서 새로운 값 추출

• 클래스 1에서 마지막 값 67을 추출 → pg.add([67, 0])
• 현재 max_value = 67로 갱신
• 우선순위 큐(pg) 상태: [(48, 1), (54, 2), (67, 0)]

2-17) 최소값과 최대값 차이 계산

• 현재 최소값은 48, 최대값은 67이므로, 차이는

  67 - 48

  = 19.

• answer = 2 (변경 없음)

2-18) 클래스 2에서 마지막 값 추출

• 클래스 2에서 마지막 값 68을 추출 → pg.add([68, 1])
• 현재 max_value = 68로 갱신
• 우선순위 큐(pg) 상태: [(54, 2), (67, 0), (68, 1)]

2-19) 최소값과 최대값 차이 계산

• 현재 최소값은 54, 최대값은 68이므로, 차이는

  68 - 54

  = 14.

• answer = 2 (변경 없음)

2-20) 클래스 3에서 더 이상 학생이 없으므로 종료

• 최종 결과: 최소 차이는 answer = 2.