컴퓨터 개론 - 기본 데이터구조

1. 선형구조

• 쌓여진 접시들을 위에서부터 아래로 사용하는 것 같이 같이 놓인 순서와 사용하는 순서가 다른 구조도 선형구조

1) 행렬과 레코드

(1) 행렬 (Array)

• 수정이 빈번하지 않은 경우와 통계처리에 이용
• 행렬은 동일한 유형의 데이터 구조(=동질성 자료구조)가 대다수 존재할 때 활용
• 레코드는 서로 다른 유형의 데이터 구조(=이질성 자료구조)로 자료처리에 많이 사용
• 예) “학번+성명+주소+전화번호+이메일 주소”

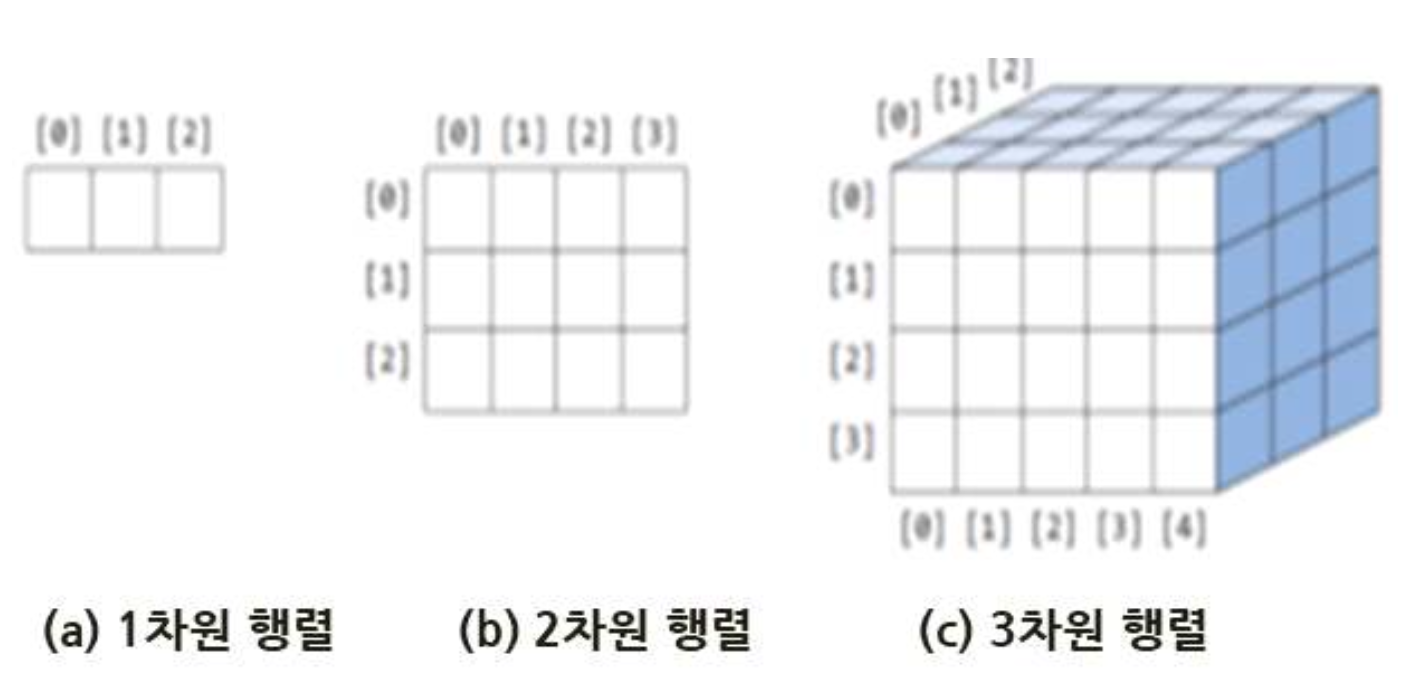
(2) C언어에서

• 1차원a(2), 2차원b(2,3) 및 3차원c(2,3,4)

2) 리스트 구조, 그리고 스택과 큐

(1) 선형리스트(List)

• 삽입과 삭제가 용이한 선형구조
• 노드(데이터) + 링크(후속 노드 지칭)
• 순서로 나열된 데이터의 모임
• 헤드포인터와 테일 포인터

(2) 스택(Stack)

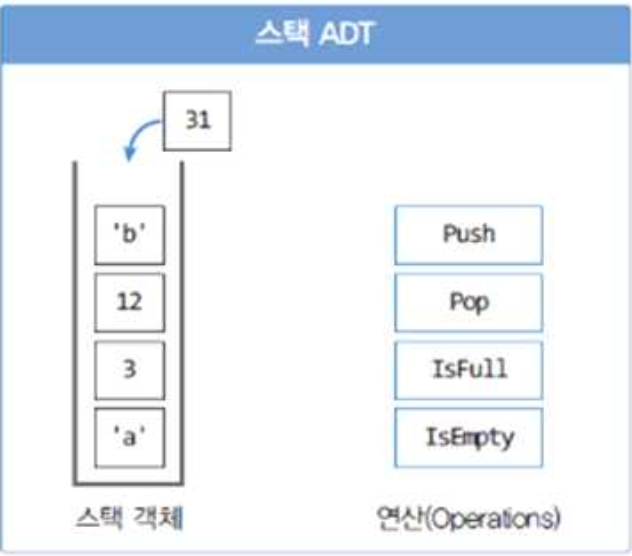
• Top과 Bottom이 존재, 새로운 항목을 스택에 삽입할 경우 맨위(Top)에다 쌓고 스택에서 한 항목을
  가져갈 때도 맨위에 있는 항목을 가져감
• LIFO(Last In First Out)구조 : 후입 선출 구조
• “Push”,”Pop”연산, “Isfull”, “IsEmpty” 연산
• 이용 : 시스템 복귀주소, 인터럽트
• 스택의 추상 데이터 형 (ADT)

(3) 큐(Queue)

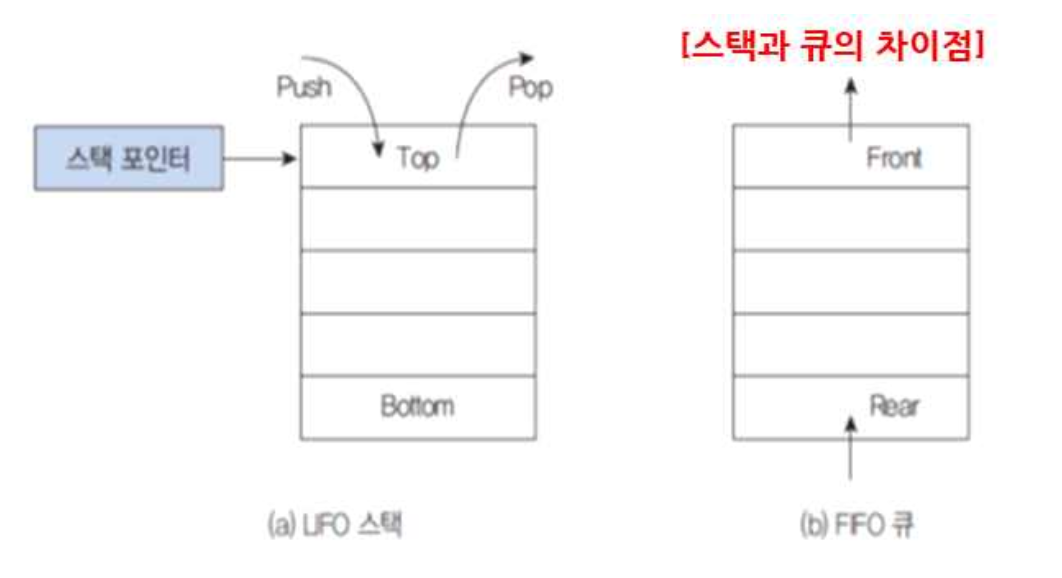
• 대기행렬 : 큐의 맨앞을 프론트 포인트(삭제가 일어나는 곳), 그리고 맨뒤를 리어 포인터 (삽입이 일어나는 곳)
• FIFO(First In First Out)구조 : 선입 선출 구조
• 이용 : 작업 스케일링, 프린터 스풀링

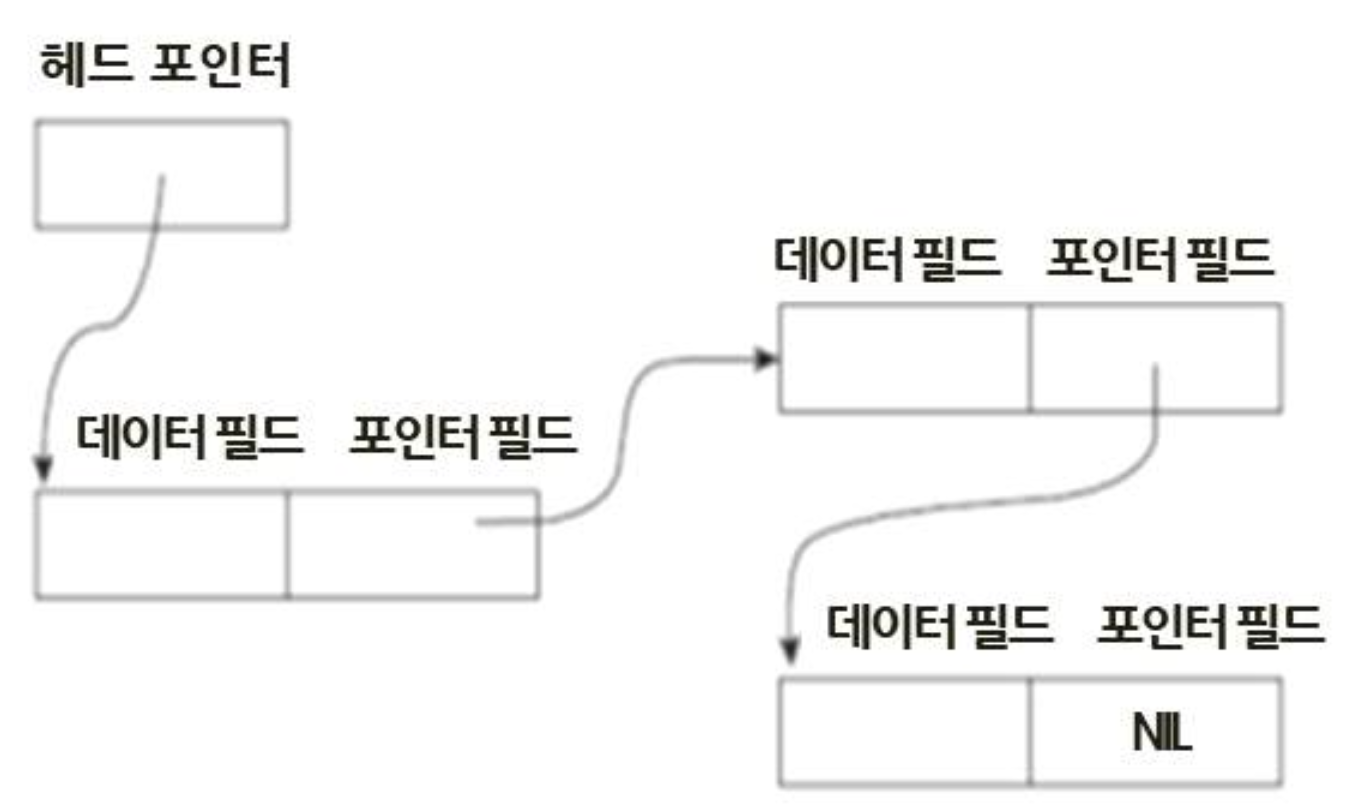
3) 연결리스트

• 노드(Node)와 포인터(Pointer)를 이요하여 리스트의 각 항목을 순차적으로 연결
• 헤드 포인터(Head Pointer), NIL 포인터

• 행렬을 이용하면 Garbage가 발생하여 문제점 도출

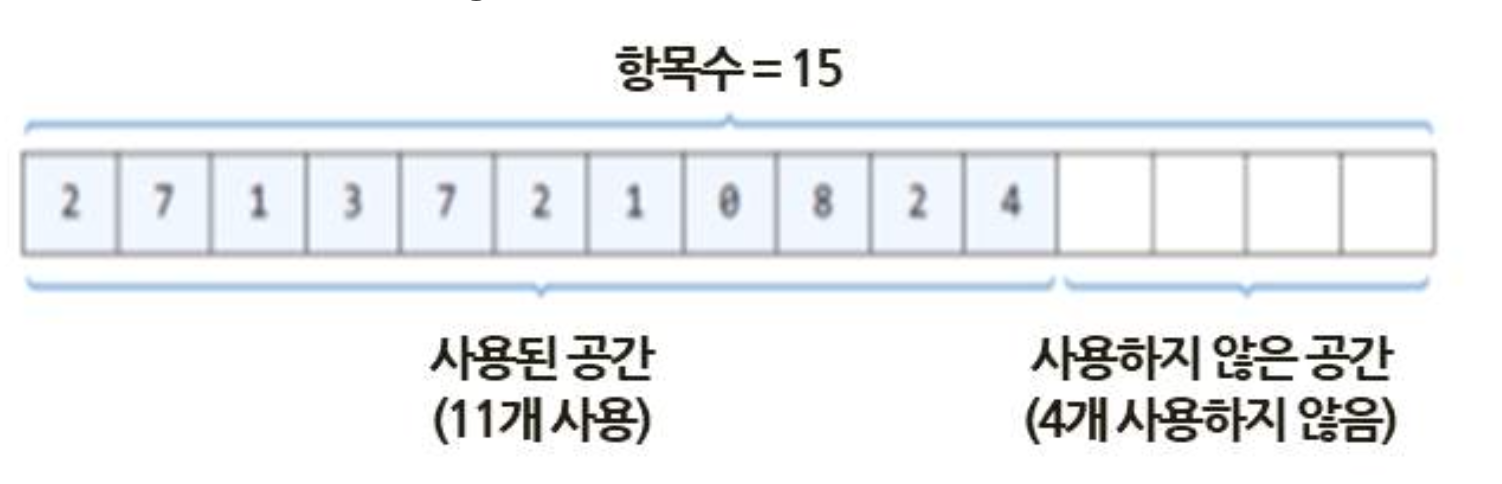
행렬을 표현 시 문제점은 연결리스트로 해결

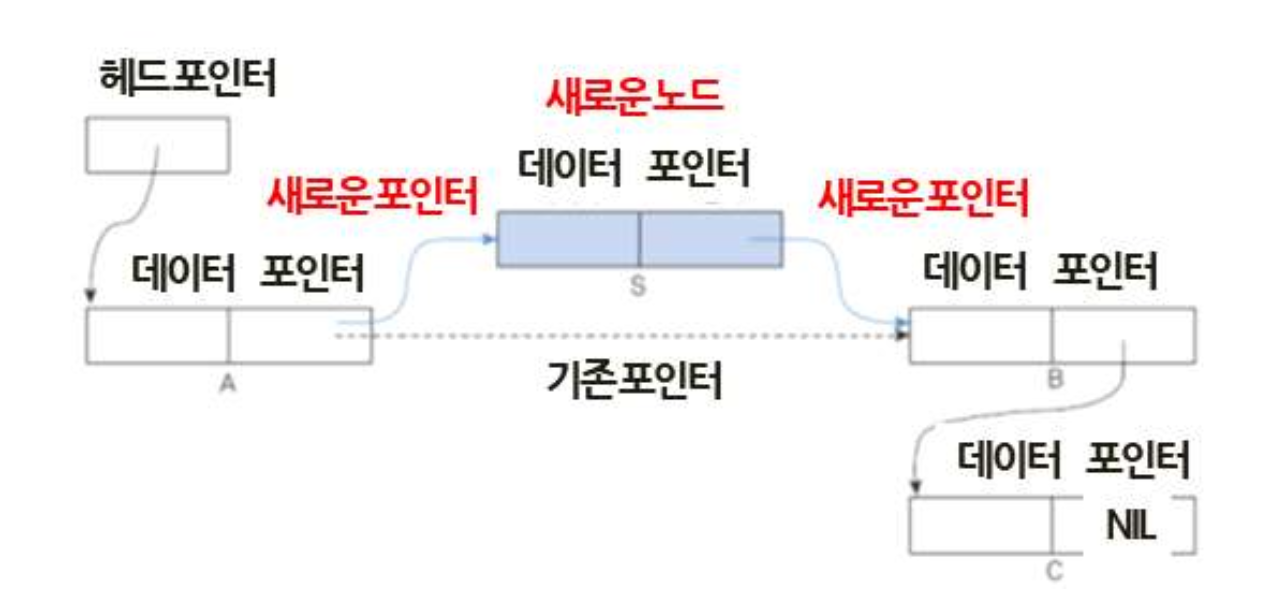
(1) 연결리스트에서 새로운 노드의 삽입(Insertion)

• 각 노드는 두개의 필드(Data, Pointer)로 구성
• 노드 A와 B사이에 새로운 노드 S 삽입시 포인터만 수정

  S.Pointer = A.Ponter
  A.Pointer = Addr(s)

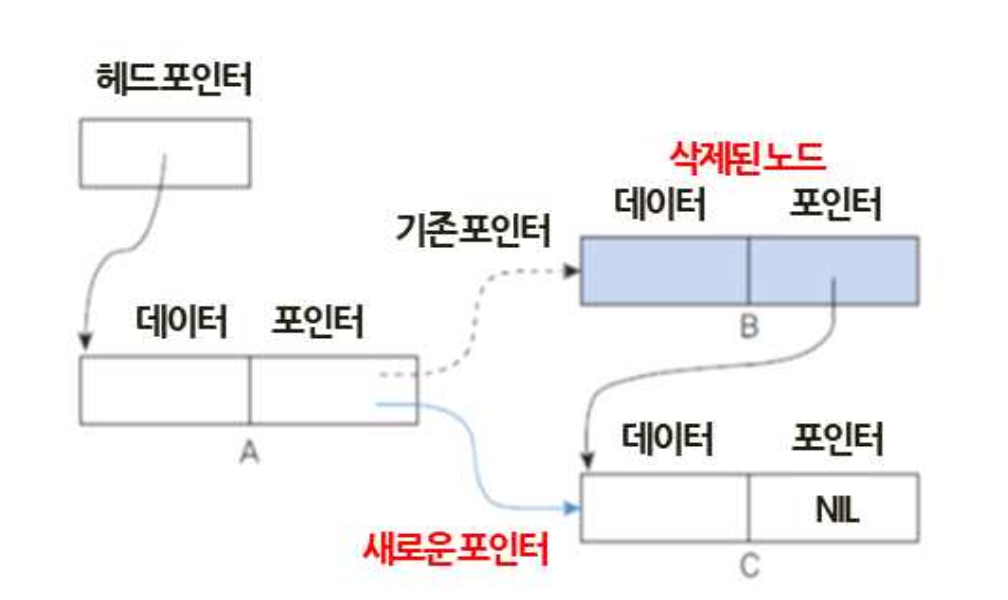
(2) 연결리스트 노드 삭제

• 연결리스트에서 노드를 삭제(Delete)는 삭제노드 바로전 노드의 포인터만 수정
• 노드B를 연결리스트에서 삭제

  A.Pointer = B.Pointer

2. 비선형구조

• 집안의 가계도나 회사의 조직도는 일직선상으로 나타낼수 없는 경우에 나타내는 방법

1) 트리와 그래프

(1) 트리(Tree)

• 트리는 연결(Connected)되고 사이클이 없는(Cycle Free) 그래프

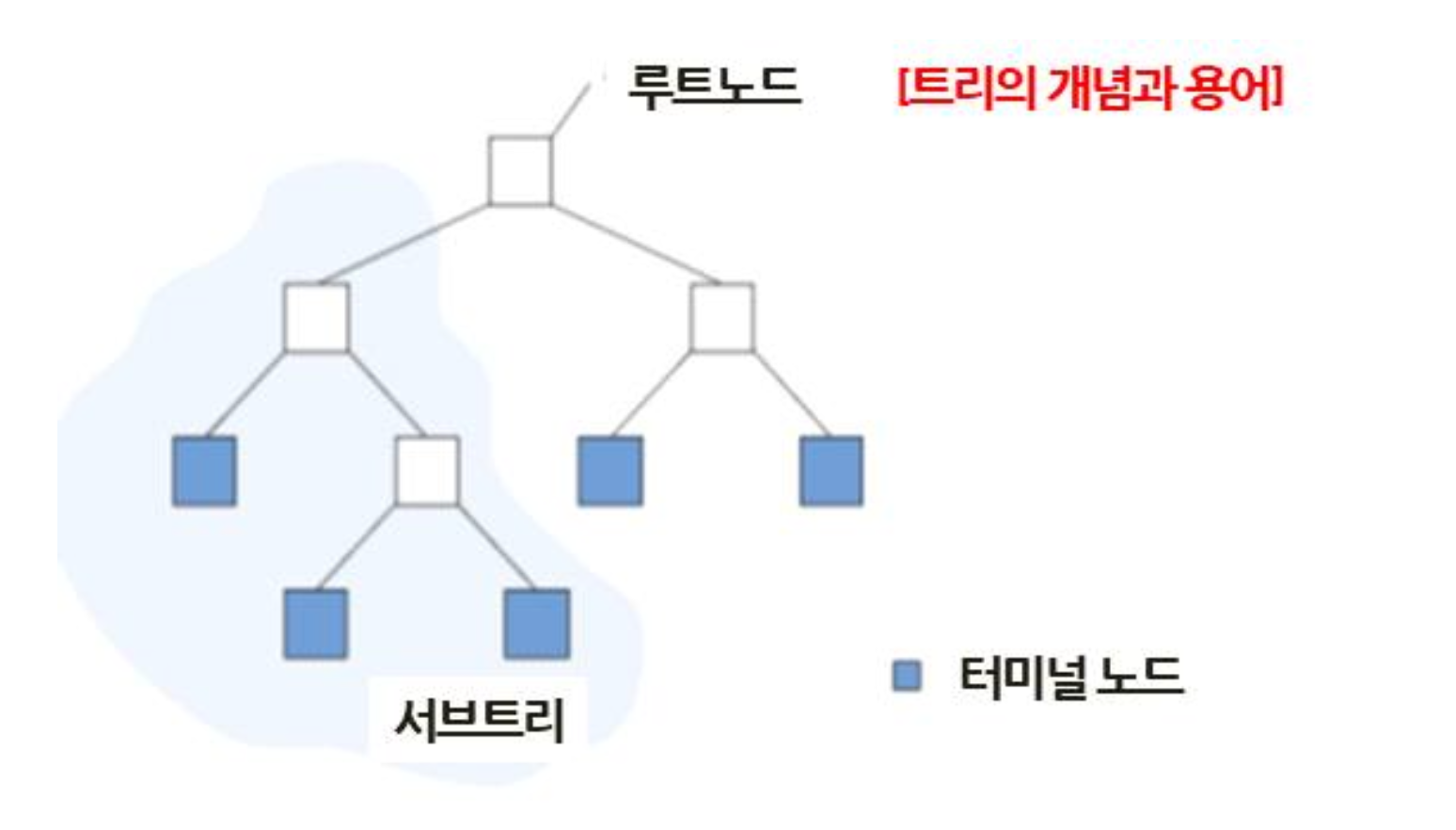
(1-1) 노드(Node)

• 루트 노드(Root Node), 자식 노드(Children Node), 부모 노드(Parent Node), 형제 노드(Siblings)
• 서브 트리(Subtree), 터미널 노드 또는 리프노드, 트리의 깊이(Depth)

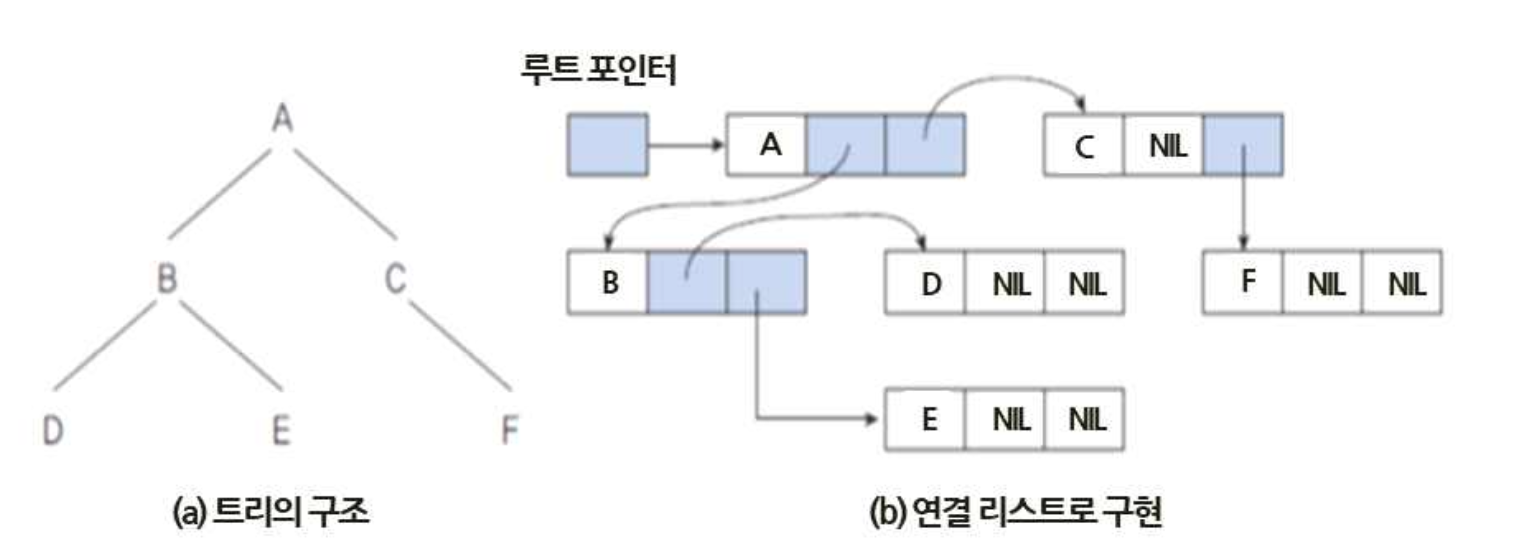
(2) 이진 트리(Binary Tree)

• 이진 트리는 2개 이하의 자(Child) 노드를 가진 트리
• 이진 트리의 노드구조 : 이중 링크리스트로 표현

• 포인터를 이용한 이진 트리의 표현 예

(3) 그래프

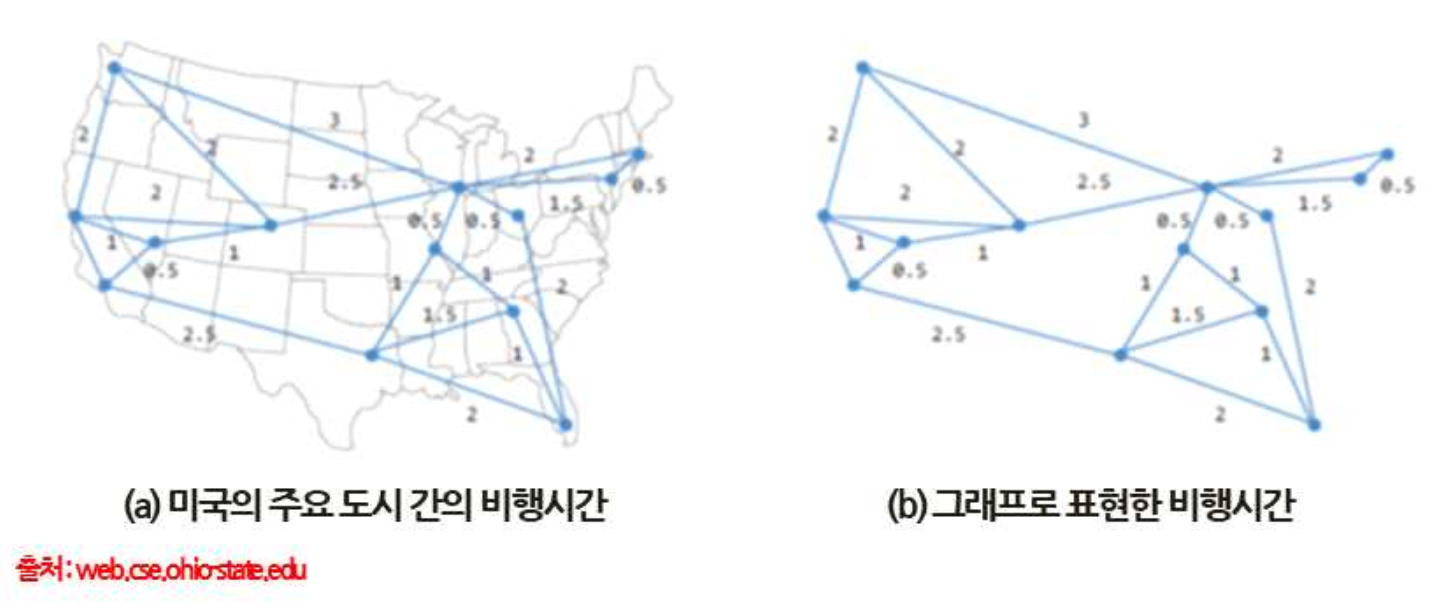
• 예) 도시간의 연결, 컴퓨터 네트워크, 도로망의 연결, 전력 망과 수도 망등의 네트워크
• 도시간의 비행시간을 보여주는 그래프의 예