그래프

1. 그래프

• 연결되어 있는 객체간의 관계를 표현하는 자료구조
• 아주 일반적인 자료구조 (트리도 그래프의 일종이라고 볼수 있음)

1) 예

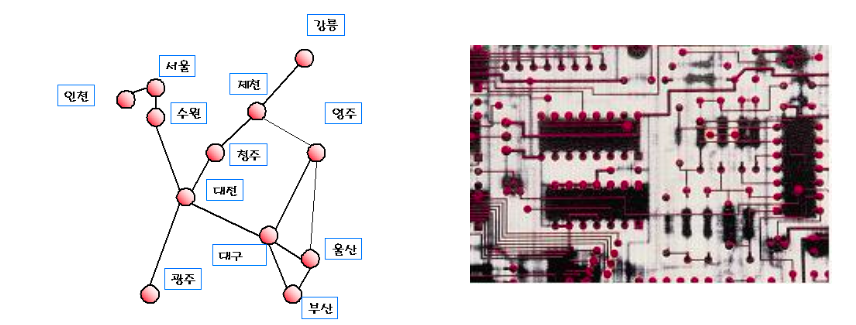
• 전기회로, 프로젝트관리, 지도에서 도시들의 연결

2) 그래프 이론

• 그래프를 문제해결의 도구로 이용하는 연구 분야

2. 그래프의 역사

• 1800년대 오일러에 의하여 창안

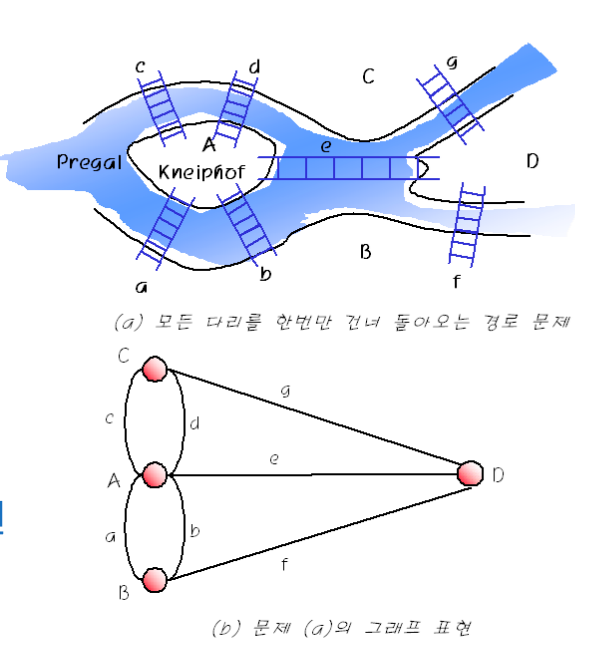
1) 오일러 문제

• 모든 다리를 한번만 건너서 처음 출발했던 장소로 돌아오는 문제

2) 문제의 핵심만을 표현

• 위치 : 정점 (node)
• 다리 : 간선 (edge)

3) 오일러 경로 : 정점에 연결된 간선의 개수가 짝수이면 존재

3. 그래프 용어

• 그래프는 ( V, E )로 표시된다.
• V 는 정점(vertices)들의 집합
• E 는 간선(edge)들의 집합
• 정점과 간선은 모두 관련되는 데이터를 가질 수 있다.

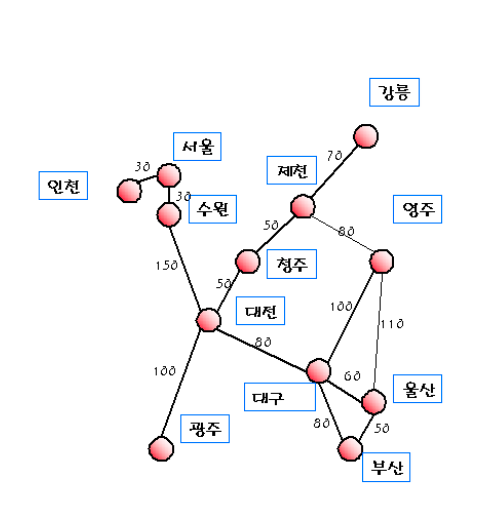
1) 예제 그래프

• 정점은 각 도시를 의미한다.
• 간선은 도시를 연결하는 도로를 의미한다.
• 간선에는 도로의 길이등의 데이터가 저장될 수 있다.

4. 그래프의 종류

• 간선의 종류에 따라 그래프는 무방향 그래프와 방향 그래프로 구분

1) 무방향 간선

• 간선을 통해서 양방향으로 갈수 있음을 나타내며 (A,B)와 같이 정점의 쌍으로 표현
• (A,B) = (B,A)

2) 방향 간선

• 방향성이 존재하는 간선으로 도로의 일방통행길과 마찬가지로 한쪽 방향으로만 갈 수 있음을 나타냄
• <A,B>로 표시
• <A,B> != <B,A>

5. 그래프 용어

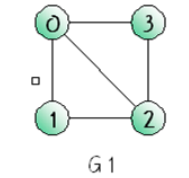
1) 인접 정점 (adjacent vertex)

• 간선에 의해 연결된 정점
• 정점 0와 정점 1

2) 차수 (dgree)

• 그 정점에 연결된 다른 정점의 개수
• 정점 0의 차수는 3

3) 경로 (path)

• 정점의 나열로 표현
• 단순 경로 : 0,1,2,3
• 사이클 : 0,1,2,0

4) 경로의 길이

• 경로를 구성하는데 사용된 간선의 수

5) 완전 그래프

• 모든 정점이 연결되어 있는 그래프

6. 그래프 ADT

• 객체 : 정점의 집합과 간선의 집합
• 연산 :

  create_graph() ::= 그래프를 생성
  init(g)        ::= 그래프 g를 초기화
  insert_vertex(g,v) ::= 그래프 g에 정점 v를 삽입
  insert_edge(g,u,v) ::= 그래프 g에 간선 (u,v)를 삽입
  delete_vertex(g,v) ::= 그래프 g에 정점 v를 삭제
  delete_edge(g,u,v) ::= 그래프 g에 간선 (u,v)를 삭제
  is_empty(g)    ::= 그래프 g가 공백 상태인지 확인
  adjacent(v)    ::= 정점 v에 인접한 정점들의 리스트를 반환
  destory_graph(g) ::= 그래프 g를 제거

• 그래프에 정점을 추가하려면 insert_vertex 연산을 사용
• 간선을 추가하려면 insert_edge 연산을 사용

7. 그래프 표현 방법

1) 그래프를 표현하는 2가지 방법

• 인접행렬 : 2차원 배열 사용 표현
• 인접리스트 : 연결리스트를 사용 표현

2) 인접행렬 방법

• if(간선 (i,j)가 그래프에 존재) M[i][j] = 1
• 그렇지 않으면 M[i][j] = 0

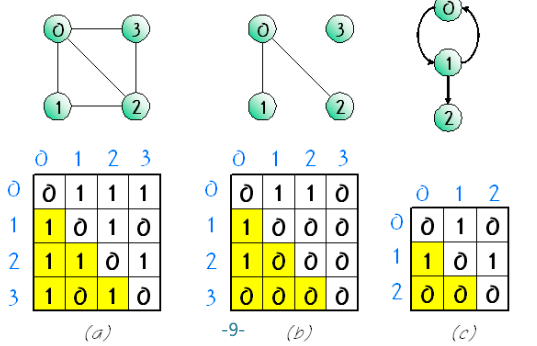
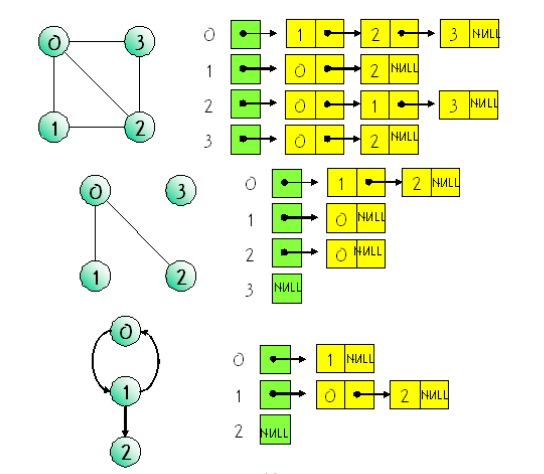
3) 인접리스트 방법

• 각 정점에 인접한 정점들을 연결리스트로 표현