그래프 - 탐색
1. 그래프 탐색
- 그래프 탐색은 그래프의 가장 기본적인 연산
- 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한번씩 방문
- 많은 문제들이 단순히 그래프의 노드를 탐색하는 것으로 해결
2. 그래프 탐색 (cont)
1) 그래프 탐색의 2가지 바업
- 깊이 우선 탐색 (DFS : depth - first search)
- 너비 우선 탐색 (BFS : breadth - frist search)
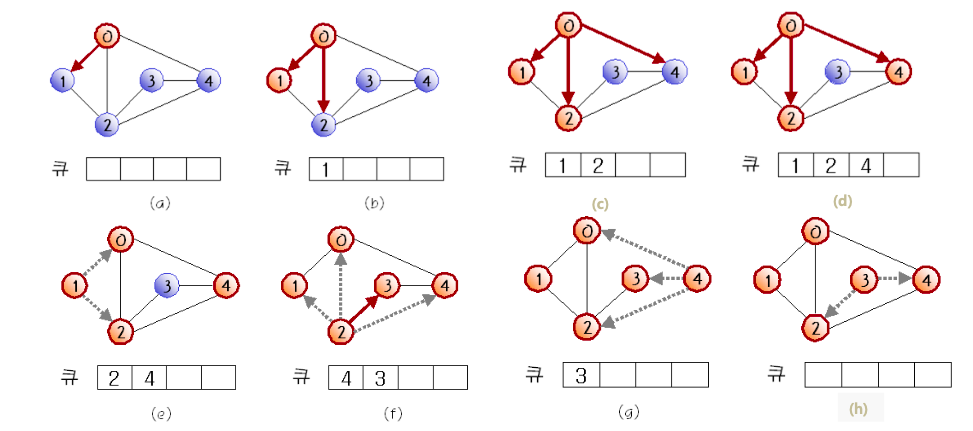
2) 깊이 우선 탐색
- 미로를 탐색할 때 한 방향으로 갈수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로
돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
2-1) DFS 알고리즘
depth_frist_search(v)
v를 방문되었다고 표시;
for all u ∈ (v에 인접한 정점) do
if(u가 아직 방문되지 않았다면)
then depth_first_search(u)
2-2) DFS 프로그램
// 인접 행렬로 표현된 그래프에 대한 깊이 우선 탐색
void dfs_mat(GraphType *g, int v)
{
int w;
visited[v] = true; // 정점 v의 방문 표시
printf("%d ", v); // 방문한 정점 출력
for(w=0; w<g->n; w+=){ // 인접 정점 탐색
if( g -> adj_mat[v][w] && !visited[w])
def_mat(g,w); // 정점 w에서 DFS 새로시작
}
}
// 인접 리스트로 표현된 그래프에 대한 깊이 우선 탐색
void dfs_list(GraphType *g, int v)
{
GraphNode *w;
visited[v] = true; // 정점 v의 방문 표시
printf("%d ", v) // 방문한 정점 출력
for(w= g-> adj_list[v]; w; w= w->link) // 인접 정점 탐색
if(!visited[w->vertex])
dfs_list(g, w-> vertext); // 정점 w에서 DFS 새로시작
}
3) 너비 우선 탐색 (BFS)
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
- 큐를 사용하여 구현됨
3-1) BFS 알고리즘
readth_first_search(v)
// v를 방문되었다고 표시
// 큐 Q에 정점 v를 삽입;
while( not is_empty(Q)) do
// Q에서 정점 w를 삭제
for all u ∈ (w에 인접한 정점) do
if( u가 아직 방문되지 않았으면)
then // u를 큐에 삽입
// u를 방문되엇다고 표시
3-2) BFS 프로그램
void bfs_mat(GraphType *g, int v)
{
int w;
QueueType q;
init(&q); // 큐 초기화
visited[v] = true; // 정점 v방문 표시
printf("%d ",v); // 정점 출력
enqueue(&q, v); // 시작 정점을 큐애 저장
while(!is_empty(&q)){
v = dequeue(&q) // 큐에서 정점 추출
for( w = 0 ; w< g-> n ; w++){ // 인접 정점 탐색
if( g -> adj_mat[v][w] && !visited[w]){
visited[w] = true;
printf("%d ", w);
enqueue(&q, w); // 방문한 정점을 큐에 저장
}
}
}
}
3. 연결 성분 찾기
- 최대로 연결된 부분 그래프들을 찾는 것
- 그래프 참색으로 찾을 수 있다.
visted[i] = count;
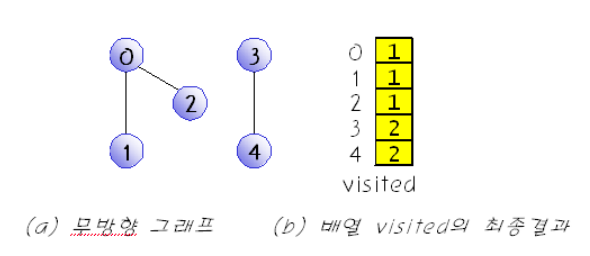
void find_connected_component(GraphType *g)
{
int i;
count = 0;
for(i = 0; i< g->n ; i++){
if( !visited[i] ){ // 방문 되지 않았으면
count ++;
dfs_mat(g,i)
}
}
}
4. 신장 트리
- 그래프내의 모든 정점을 포함하는 트리
- 신장 트리는 모든 정점들이 연결되어 있어야 하고 또한 사이클을 포함해서는 안된다.
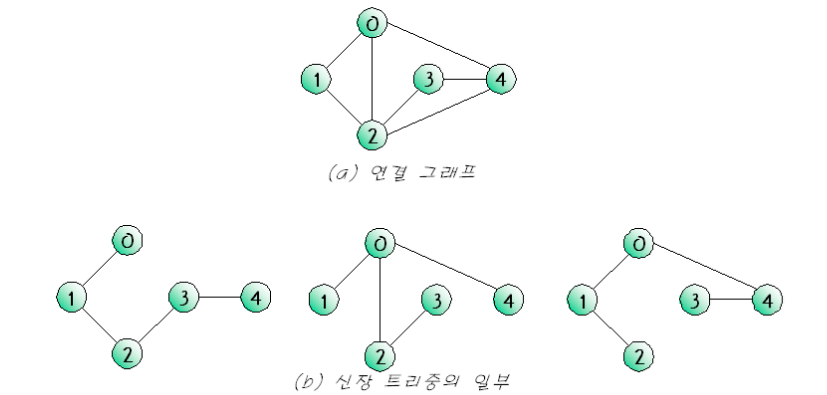
1) 신장 트리 알고리즘
depth_first_search(v)
// v를 방문되었다고 표시
for all u ∈ (v에 인접한 정점) do
if(u가 아직 방문되지 않았으면)
then // (v,u)를 신장 트리 간선이라고 표시;
depth_first_search(u)
2) 신장 트리의 용도
- 통신 네트워크 구축 : 최소의 링크를 사용하여 네트워크를 구축하고 싶은 경우
5. 최소 비용 신장 트리 (MST : minimu spanning tree)
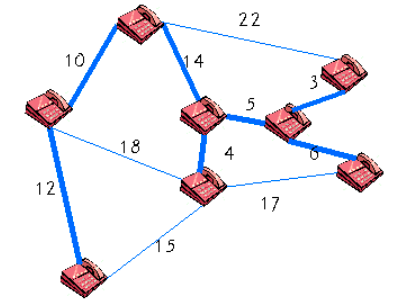
- 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 신장 트리
1) 응용
1-1) 도로 건설
- 도시들을 모두 연결하면서 도로의 길이가 최소가 되도록 하는 문제
1-2) 전기 회로
- 단자들을 모두 연결하면서 전선의 길이가 가장 최소가 되도록 하는 문제
1-3) 통신
- 전화선의 길이가 최소가 되도록 전화 케이블 망을 구성하는 문제
1-4) 배관
- 파이프를 모두 연결하면서 파이프의 총 길이가 최소가 되도록 연결하는 문제
2) MST 알고리즘
2-1) 2가지의 대표적인 알고리즘
2-2) 탐욕적인 방법 (greedy method)
- 알고리즘 설계에서 있어서 중요한 기법 중의 하나
- 결정을 해야 할때마다 그 순간에 가장 좋다고 생각되는 것을 해답으로 선택함으로써 최종적인 해답에 도달
- 탐욕적인 방법은 항상 최적의 해답을 주는지 반드시 검증해야 함
- Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명
8. kruskal의 MST 알고리즘의 구현
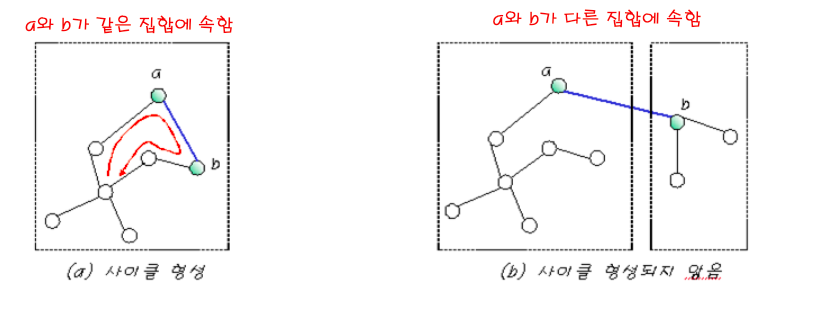
1) union - find 알고리즘
- 집합들의 합집합을 구하고 집합의 원소가 어떤 집합에 속하는지를 계산하는 알고리즘
- 여러가지 방법으로 구현이 가능
- Kruskal의 MST 알고리즘에서 사이클 검사에 사용된다.
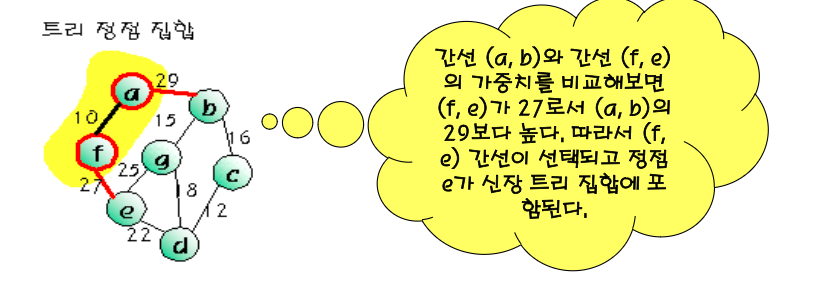
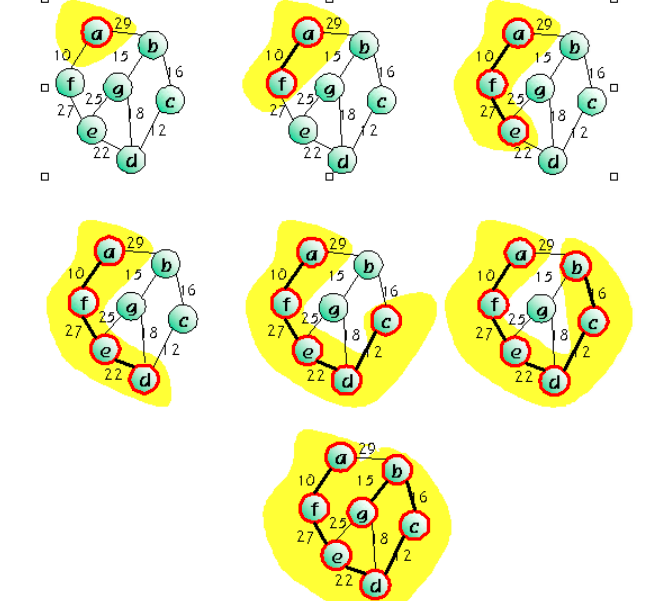
9. Prim의 MST 알고리즘
- Prim의 알고리즘은 시작 정점에서부터 출발하여 신장 트리 집합을 단계적으로 확장해나가는 방법
- 시작 단계에서는 시작 정점만이 신장 트리 집합에 포함
- 앞 단계에서 만들어진 신장 트리 집합에, 인접한 정점들 중에서 최저 간선으로 연결된 정점을 선택하여 트리를 확장
- 이 과정은 트리가 n-1개의 간선을 가질때 까지 계속된다.
10. 최단 경로 알고리즘
- 최단 경로 문제는 네트워크에서 정점 i와 정점 j를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로를
찾는 문제
- 간선의 가중치는 비용, 거리, 시간 등을 나타낸다.
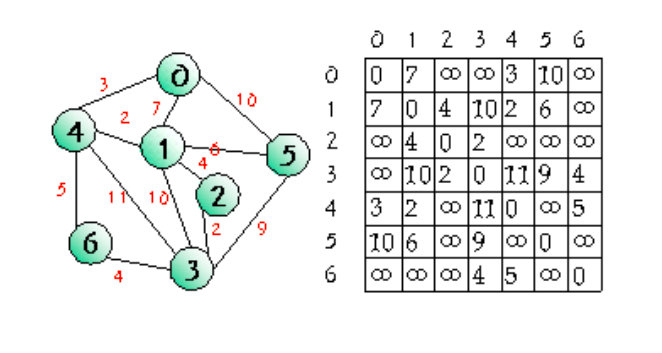
1) Dijkstra의 최단 경로 알고리즘
- Dijkstra의 최단 경로 알고리즘은 네트워크에서 하나의 시작 정점으로부터 모든 다른 정점까지의 최단 경로를 찾는
알고리즘
- 집합 S : 시작 정점 v로부터의 최단경로가 이미 발견된 정점들의 집합
- distance 배열 : 최단 경로를 알려진 정점만을 통하여 각 정점까지 가는 최단경로의 길이
- 매단계에서 가장 distance 값이 적은 정점을 S에 추가
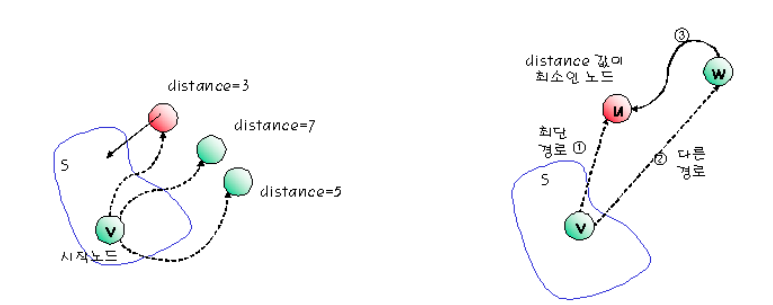
- 매 단계에서 새로운 정점이 S에 추가되면 distance 값을 갱신
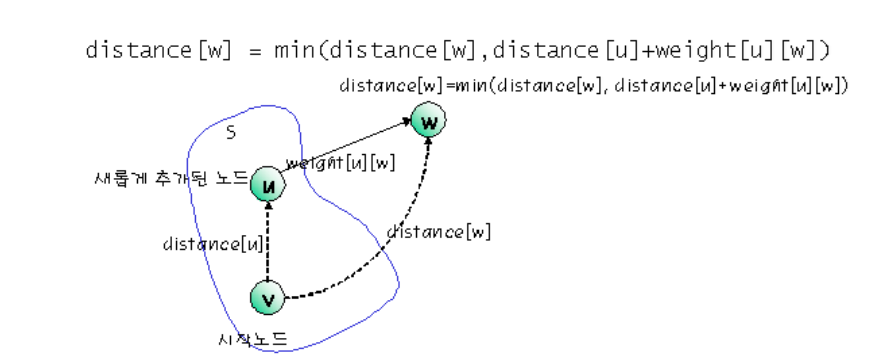
2) Dijkstra의 최단 경로 알고리즘
// 입력 : 가중치 그래프 G, 가중치는 음수가 아님
// 출력 : distance 배열, distance[u]는 v에서 u까지의 최단 거리이다.
shortest_path(G,V)
S <-{V}
for 각 정점 W ∈ G do
distance[w] <- weight[V][W]
while 모든 정점이 S에 포함되지 않으면 do
u <- 집합 S에 속하지 않은 정점 중에서 최소 distance 정점;
S <- S U {u}
for u에 인접하고 S에 있는 각 정점 z do
if distance[u] + weight[U][Z] < distance[Z]
then distance[Z] <- distance[u] + weight[u]{z}
11. 위상 정렬
- 방향 그래프에서 간선
<u,v>가 있다면 정점 u는 정점 v를 선행한다고 말한다.
- 방향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것을 방향 그래프의
위상정렬 이라고 한다.
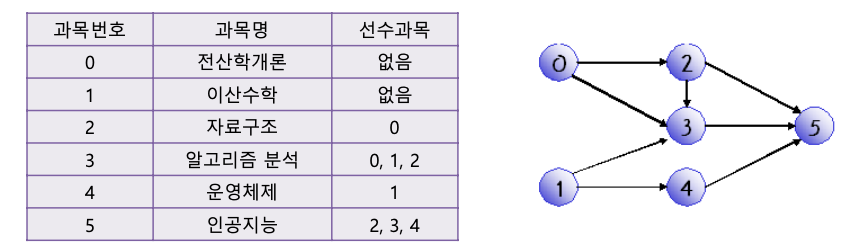
- 위상 정렬 : (0,1,2,3,4,5), (1,0,2,3,4,5)
- (2,0,1,3,4,5)는 위상 정렬이 아니다. 왜냐하면 2번 정점이 0 번 정점 앞에 오기 때문
- 간선
<0,2>이 존재하기 때문에 0번 정점이 끝나야 만이 2번 정점을 시작할 수 있다.
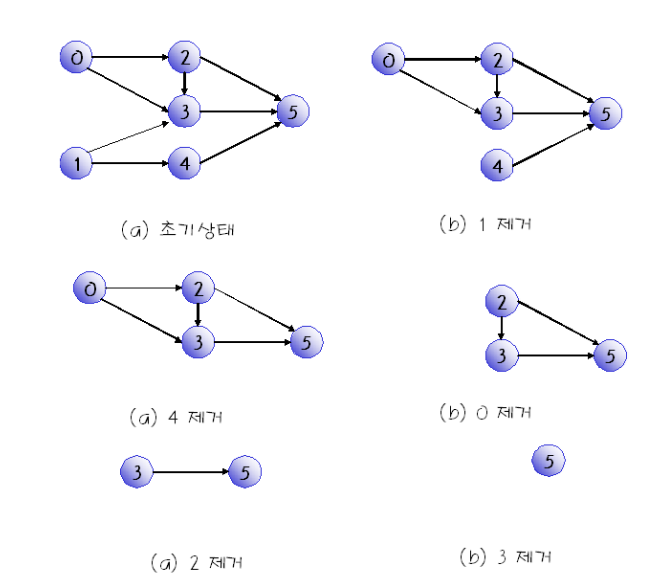
1)
// 입력 : 그래프 G = (V,E)
// 출력 : 위상 정렬 순서
topo_sort(G)
for i <- 0 to do
if( 모든 정점이 선행 정점을 가지면 )
then 사이클이 존재하고 위상 정렬 불가;
선행 정점을 가지지 않는 정점 v 선택;
v 출력
v와 v에서 나온 모든 간선들을 그래프에서 삭제;














댓글남기기