바킹독의 실전 알고리즘 0x04강 ( 연결리스트 )

목차

• 0x00 정의와 성질
• 0x01 기능과 구현
• 0x02 STL list
• 0x03 연습 문제

1. 정의와 성질

• 원소들을 저장할 때 그 다음 원소가 있는 위치를 포함시키는 방식을 저장하는 자료구조
• 원소들은 이곳 저곳에 흩어져 있음

1. k번째 원소를 확인/변경하기 위해 O(K)가 필요
2. 임의의 위치에 원소를 추가/ 임의 위치의 원소 저게는 O(1)
3. 원소들이 메모리 상에 연속해있지 않아 Cache hit rate가 낮미ㅏㄴ 할당이 다소 쉬움

1) 연결 리스트의 종류

1-1) 단일 연결 리스트

• 걱 원소가 자신의 다음 원소의 주소를 들고 있는 연결리스트

1-2) 이중 연결 리스트

• 각 원소가 자신의 이전 원소와 다음 원소의 주소를 둘 다 들고 있음
• 단일 연결 리스트는 이전 원소가 무엇인지 알 수 없는데 이중연결 리스트에서는 알 수 있음
• 다만, 원소가 가지고 있어야 하는 정보가 한 개 더 추가되니 메모리를 더 쓴다.

1-3) 원형 연결 리스트

• 끝이 처음과 연결 되어 있음
• 각 원소가 이전과 다음 원소의 주소를 모두 들고 있어도 상관 없음

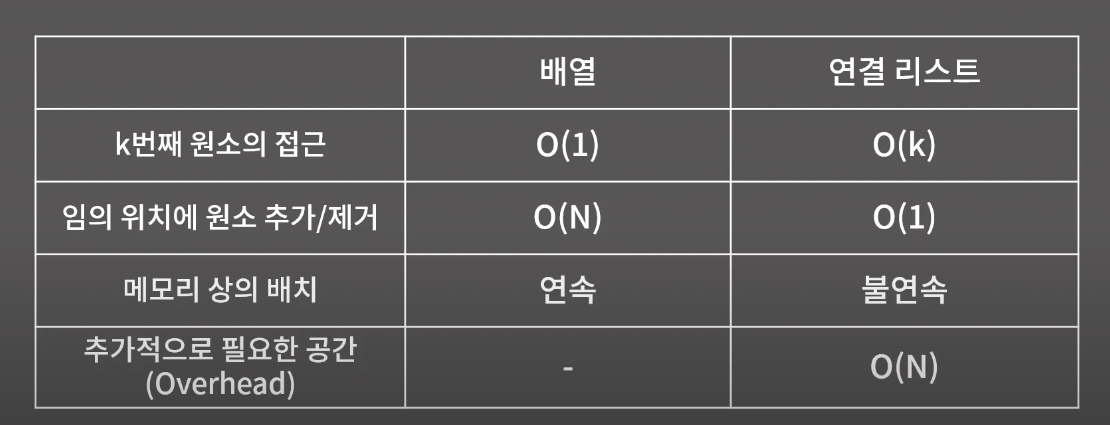
2) 배열 vs 연결 리스트

• 배열과 연결리스트는 선형 자료 구조

2. 기능과 구현

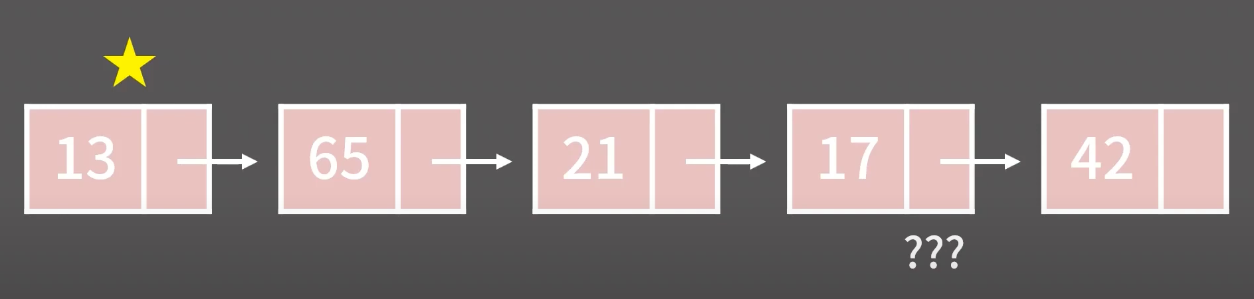
1) 임의의 위치에 있는 원소를 확인/변경, O(N)

• 배열과는 다르게 임의의 위치에 있는 원소로 가기 위해서는 그 위치에 도달할 때까지 첫번째 부터 순차적 방문

2) 임의의 위치에 원소를 추가, O(1)

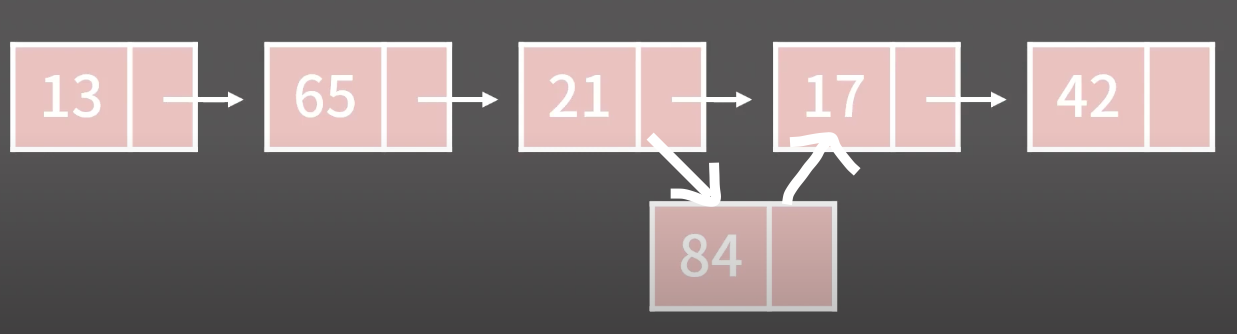
• 21 뒤에 84를 추가하고 싶다고 할 때 , 21과 84에서 다음 원소의 주소만 변경을 해주면 되기 때문
• 추가 하고 싶은 주소를 알고 있을 경우에만 O(1)

3) 임의의 위치의 원소를 제거, O(1)

• 65에서 17만 가르키면 됨
• 그런 다음에 21이 들어있는 원소는 메모리 누수를 막기 위해 메모리에서 없애줄 필요가 있음

4) 연결 리스트의 구현

• 야매 연결 리스트 (정석 x)

  const int MX = 1000005;
  int dat[MX], pre[MX], nxt[MX];
  int unused = 1;

  fill(pre, pre+MX, -1);
  fill(nxt, nxt+MX, -1);

• 주어진 연결 리스트는 13, 65, 21, 17

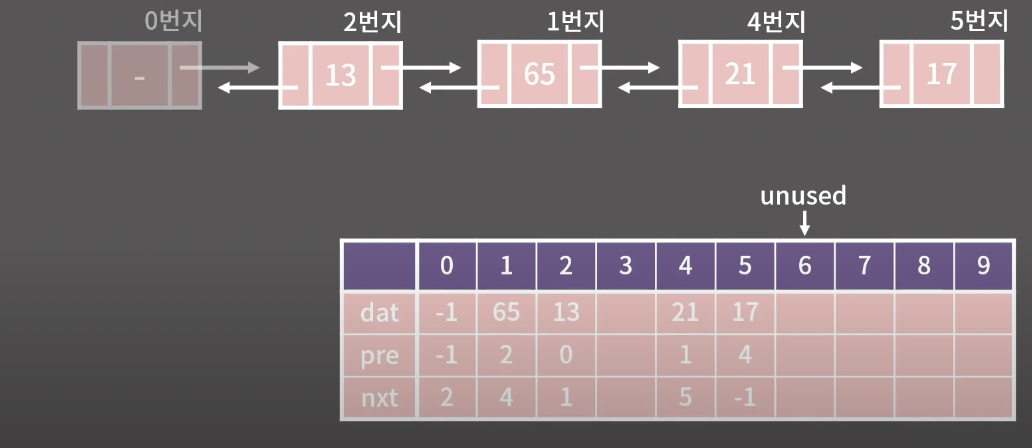
4-1) traverse 함수

void traverse() {
  int cur = nxt[0];
  while(cur != -1){
    cout << dat[cur] << ' ';
    cur = nxt[cur];
  }
  cout << "\n\n";
}

4-3) insert 함수

1. 새로운 원소를 생성
2. 새 원소의 pre값에 삽입할 위치의 주소를 대입
3. 새 원소의 nxt값에 삽입할 위치의 nxt값을 대입
4. 삽입할 위치의 nxt 값과 삽입할 위치의 다음 원소의 pre값을 새 원소로 변경
5. unused 1 증가

void insert(int addr, int num){
  dat[unused] = num;
  pre[unused] = addr;
  nxt[unused] = nxt[addr];
  if(nxt[addr] != -1) pre[nxt[addr]] = unused;
  nxt[addr] = unused;
  unused++;
}

4-4) erase 함수

1. 이전 위치의 nxt를 삭제할 위치의 nxt로 변경
2. 다음 위치의 pre를 삭제할 위치의 pre로 변경

void erase(int addr){
  nxt[pre[addr]] = nxt[addr];
  if(nxt[addr] != -1) pre[nxt[addr]] = pre[addr];
}

4. 연습 문제

1) BOJ 1406번: 에디터

BackJoon Algorithm 1406 에디터 (Java)

2) 손 코딩 문제 1

2-1) 원형 연결 리스트 내의 임의의 노드 하나가 주어졌을 때 해당 List의 길이를 효율적으로 구하는 방법은?

• 동일한 노드가 나올 때 까지 계속 다음 노드로 가면 됨, 공간복잡도 O(1), 시간 복잡도 O(N)

3) 손 코딩 문제 2

3-1) 중간에 만나는 두 연결 리스트의 시작점들이 주어졌을 때 만나는 지점을 구하는 방법은?

• 일단 두 시작점 각각에 대해 끝까지 진행시켜서 각각의 길이를 구함
• 그 후 다시 두 시작점으로 돌아와서 더 긴쪽을 둘의 차이만큼 앞으로 먼저 이동시켜놓고 두 시작점이
  만날때 까지 두 시작점을 동시에 한칸씩 전진 시키면 됨.
• 공간복잡도 O(1), 시간 복잡도 O(A+B)

4) 손 코딩 문제 3

4-1) 주어진 연결 리스트 안에 사이클이 있는지 판단해라

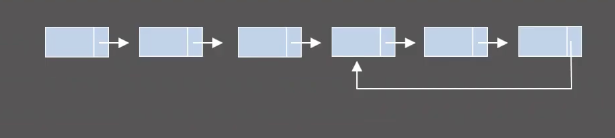
• Floyd’s cycle-finding algorithm

• 공간복잡도 O(1), 시간복잡도 O(N)

출처

[바킹독의 실전 알고리즘] 0x04강 - 연결리스트