(알고리즘) 바킹독의 실전 알고리즘 0x0B강 ( 재귀 )
바킹독의 실전 알고리즘 0x0B강 ( 재귀 )
목차
- 0x00 알고리즘 설명
- 0x01 연습 문제 1 - 거듭제곱
- 0x02 연습 문제 2 - 하노이 탑
- 0x03 연습 문제 3 - Z
1. 알고리즘 설명
1) 재귀
- 하나의 함수에서 자기 자신을 다시 호출해 작업을 수행하는 알고리즘
2) 예시
void func1(int n){
if(n == 0) return;
cout << n << ' ';
func1(n-1);
}
void func2(int n){
if(n == 0) return 0;
return n + func2( n - 1 );
}
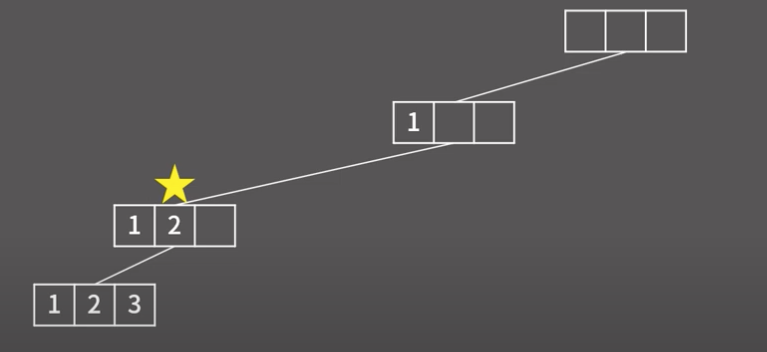
3) 수학적 귀납법

- 지금 사진의 도미노에서 제일 앞의 도미노를 쓰러트리게 되면 모든 도미노가 쓰러짐
- 그런데 왜 모든 도미노가 쓰러지는 지를 설명해보라고 한다면 두 가지 방법이 있음
3-1) 첫번째 방법
- 1번 도미노가 쓰러지면 2번 도미노가 쓰러지고
- 2번 도미노가 쓰러지면 3번 도미노가 쓰러짐
- 이런 식으로 진행되기 때문에 모든 도미노가 쓰러짐
3-2) 두번째 방법
- ‘K번 도미노가 쓰러지면 K + 1번 도미노도 쓰러진다’가 참이니까 모든 도미노가 쓰러진다.
4) 재귀 함수의 조건
- 특정 입력에 대해서는 자기 자신을 호출하지 않고 종료되어야 함 (Base condition)
-
모든 입력은 base condition으로 수렴해야 함
- 이 두조건 중 하나라도 충족하지 못하면 결과를 내지 못하고 무한히 돌아가다가 런타임 에러 발생
5) 재귀에 대한 정보 1
- 함수의 인자로 어떤것을 받고 어디까지 계산한 후 자기 자신에게 넘겨줄지 명확하게 정해야 함
- 모든 재귀 함수는 반목문만으로 동일한 동작을 하는 함수를 만들 수 있음
- 재귀는 반복문으로 구현했을 때에 비해 코드가 간결하지만 메모리/시간에서는 손해를 봄
6) 재귀에 대한 정보 2
- 한 함수가 자기 자신을 여러번 호추랗게 되면 비효율적일 수 있음
int fibo(int n){
if(n <= 1) return 1;
return fibo(n-1) + fibo(n-2);
}
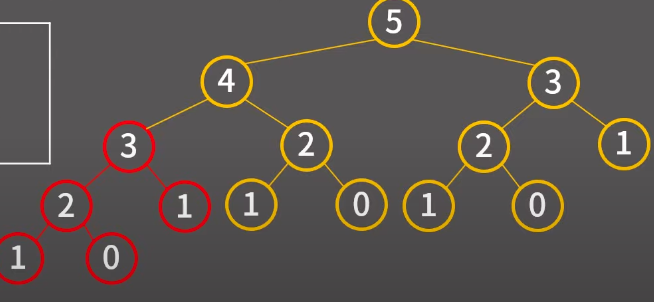
- 이미 계산 한걸 또 계산한다는 일이 아주 빈번함.
- fibo(3)을 계산하기 위해 fibo(2)와 fibo(1)을 부르고 fibo(2)는 fibo(1)과 fibo(0)을 부르는 일이 발생
- 오른쪽에서도 fibo(3)을 계산하는 것이 발생
- 시간복잡도가 커져버림
3) 재귀에 대한 정보 3
- 재귀함수가 자기 자신을 부를 때 스택 영역에 계속 누적이 됨
2. 연습 문제 1 - 거듭제곱
1) a^b mod m
int func1 (int a, int b, int m){
int val = 1;
while(b--) val *= a;
return val % m;
}
- func1(6,100,5)를 넣었을때 식이 제대로 돌아기않음
- int overflow때문
- 6^100은 int 범위를 넘어감
using ll = long long;
ll func1(ll a, ll b, ll m){
ll val = 1;
while(b--) val = val * a &% m;
return val;
}
2) BOJ 1629 : 곱셈
2-1) C
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll pow(ll a, ll b, ll m){
if( b == 1) return a % m; // base contidtion
ll val = pow(a, b/2, m);
val = val * val % ml
if( b % 2 == 0) return val;
return val * a % m;
}
int main(void){
ios::sync_with_stdio(0);
cin.tie(0);
ll a,b,c;
cin >> a >> b >> c;
cout << pow(a,b,c);
}
2-2) Java
BackJoon Algorithm 곱셈 1629 (Java)
2-3) 함수 호출 과정 분석
-
첫 번째 호출: pow(10, 11, 12)
- B가 1이 아니므로, pow(10, 11/2, 12) 즉, pow(10, 5, 12)를 호출합니다.
-
두 번째 호출: pow(10, 5, 12)
- B가 1이 아니므로, pow(10, 5/2, 12) 즉, pow(10, 2, 12)를 호출합니다.
- 세 번째 호출: pow(10, 2, 12)
- B가 1이 아니므로, pow(10, 2/2, 12) 즉, pow(10, 1, 12)를 호출합니다.
- 네 번째 호출: pow(10, 1, 12)
- B가 1이므로, 10 % 12 즉, 10을 반환합니다.
2-4) 재귀적 계산 과정
- 네 번째 호출 결과: val = 10
-
세 번째 호출 계산: 10 * 10 % 12 = 4
- B가 짝수가 아니므로, ((10 _ 10) % 12) _ 10 % 12 = 4를 반환합니다.
-
두 번째 호출 계산: 4 * 4 % 12 = 4
- B가 짝수이므로, 4 * 4 % 12 = 4를 반환합니다.
- 첫 번째 호출 계산: 4 * 4 % 12 = 4
- B가 짝수가 아니므로, ((4 * 4) % 12) * 10 % 12 = 4를 최종 반환합니다.
3. 연습 문제 2 - 하노이 탑
1) BOJ 11729번 : 하노이 탑 이동 순서
- n - 1개의 원판을 기둥 1에서 기둥 2로 옮긴다.
- n번 원판을 기둥 1에서 기둥 3으로 옮긴다.
-
n - 1개의 원판을 기둥2에서 기둥 3으로 옮긴다.
- 원판이 n-1개일 때 옮길 수 있다면 원판이 n개일 때도 옮길 수 있다.
- 원판이 1개일때 원판을 내가 원하는 곳으로 옮길수 있다.
- 우너판이 K개일 때 옮길 수 있으면 원판이 k+1개 일때도 옮길수 있다.
1-1) 함수의 정의
- 원판 n개를 a번 기둥에서 b번 기둥으로 옮기는 방법을 출력하는 함수
void func(int a, int b, int n)
1-2) base condition
- n = 1일때
cout << a << ' ' << b << '\n'
1-3) 재귀 식
- n - 1개의 원판을 기둥 a에서 기둥 6 - a - b로 옮긴다.
func(a, 6-a-b, n -1);
- n번 원판을 기둥 a에서 기둥 b로 옮긴다.
cout << a << ' ' << b << '\n'
- n - 1개의 원판을 기둥 6 - a - b에서 기둥 b로 옮긴다.
func(6-a-b, b , n-1);
- 풀예정

댓글남기기