자료 구조 - 이진트리의 순회

1. 이진 트리의 순회란?

• 계층적 구조로 저장되어있는 트리의 모든 노드를 방문하여 데이터를 처리하는 연산
• 이진 트리가 순환적으로 정의되어 구성되어있으므로 순회작업도 서브트리에 대해서 순환적으로 반복하여 완성
• 왼쪽 서브트리에 대한 순회를 오른쪽 서브트리 보다 먼저 수행

1) 순회를 위해 수행할 수 잇는 작업 정의

• 현재 노드를 방문하여 데이터를 읽는 작업 D
• 현재 노드의 왼쪽 서브트리로 이동하는 작업 L
• 현재 노드의 오른쪽 서브트리로 이동하는 작업 R

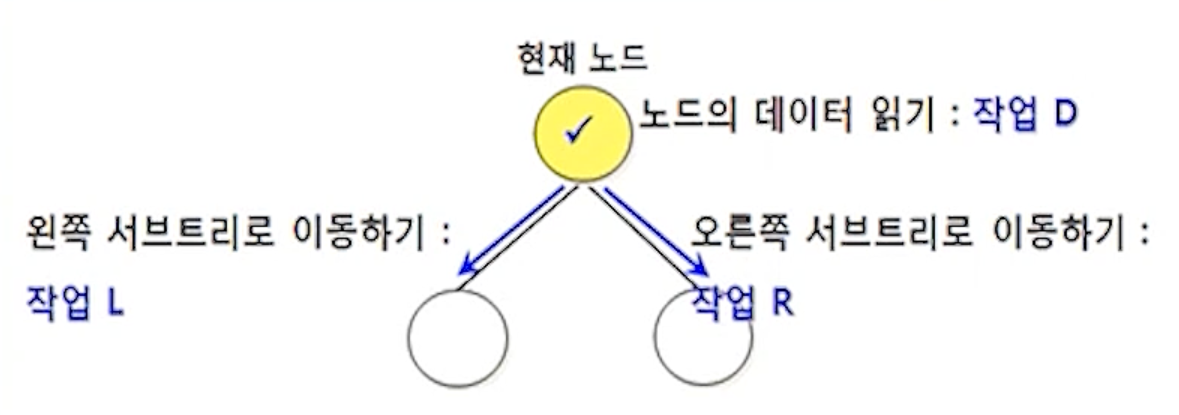
(1) 순회의 종류

• 전위 순회, 중위 순회, 후위 순회

2. 이진트리 순회 방법

1) 전위 순회

(1) 수행 방법

1. 현재 노드 n을 방문하여 처리함 : D
2. 현재 노드 n의 왼쪽 서브트리로 이동함 : L
3. 현재 노드 n의 오른쪽 서브트리로 이동함 : R

(2) 알고리즘

  preorder(T)
        if(T != null) then{
            visit T.data;
            preorder(T.left);
            preorder(T.right);
        }
  end preorder()

(3) 예

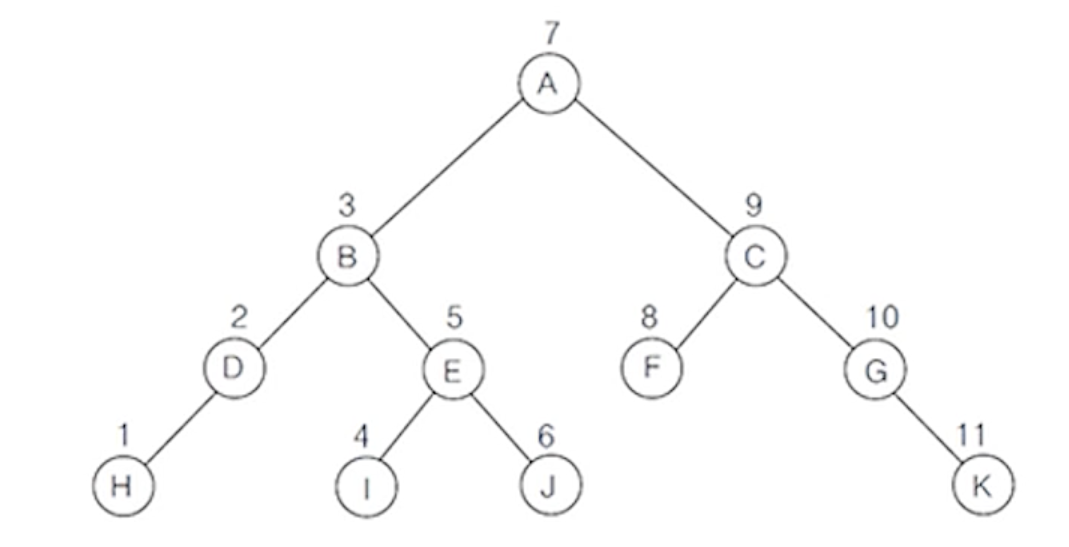
• 이진 트리의 전위 순회 경로 : A - B - D - H - E - I - J - C - F - G - K

(4) 전위 순회 과정 » A - B - D - H - E - I - J - C - F - G - K

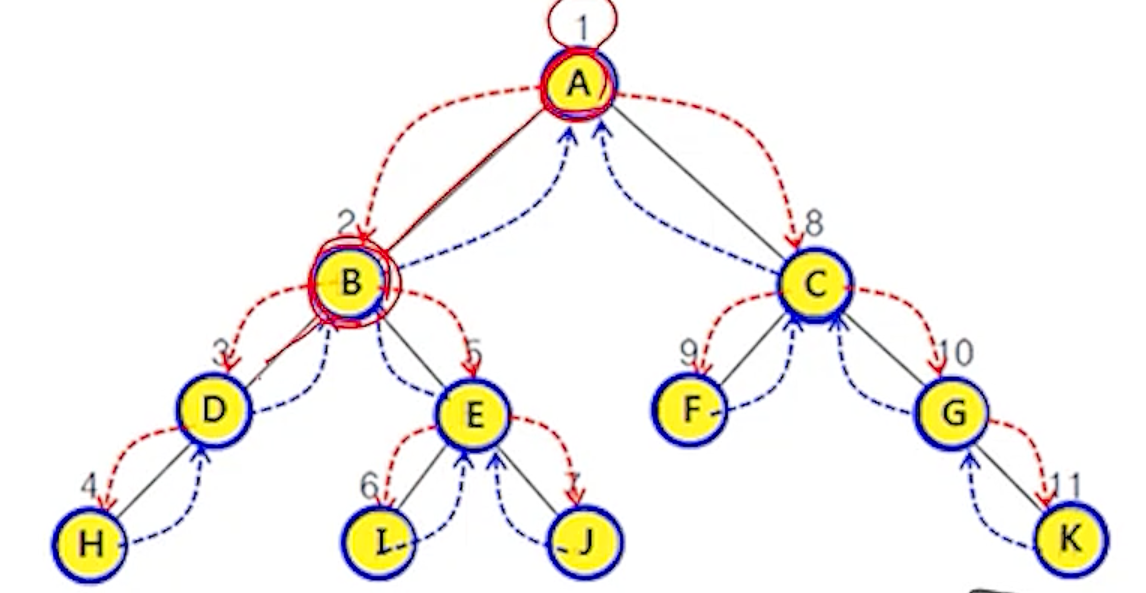
(4-1)

• 노드 A : 루트 A에서 전위 순회를 시작하여 현재 노드 A의 데이터를 읽음 (D)
• 노드 A -> 노드 B : 왼쪽 서브트리인 노드 B로 이동함 (L)

(4-2)

• 노드 A -> 노드 B : 현재 노드 B의 데이터를 읽음 (D)
• 노드 A -> 노드 B -> 노드 D : 현재 서브트리인 노드 D로 이동 (L)

(4-3)

• 노드 A -> 노드 B -> 노드 D : 현재 노드 D의 데이터를 읽음 (D)

(4-4)

• 노드 A -> 노드 B -> 노드 D -> 노드 H : 현재 노드 D의 왼쪽 단말노드 H의 데이터를 읽음 (D)
• 노드 A -> 노드 B -> 노드 D -> 공백노드 : 노드 D의 오른쪽 노드인 공백노드를 읽는 것으로
  노드 D에 대한 DLR 순회가 끝남
• 노드 A -> 노드 B <- 노드 D : 노드 D의 순회가 끝났으며 이전 경로인 노드 B로 돌아감
• 노드 A -> 노드 B -> 노드 E : 현재 노드 B의 오른쪽 서브트리인 노드 E로 이동함 (R)

(4-5)

• 노드 A -> 노드 B -> 노드 E : 현재 노드 E의 데이터를 읽음 (D)

(4-6)

• 노드 A -> 노드 B -> 노드 E -> 노드 I : 노드 E의 왼쪽 단말 노드 I의 데이터를 읽음 (L)

(4-7)

• 노드 A -> 노드 B -> 노드 E -> 노드 J : 노드 E의 오른쪽 단말 노드 J의 데이터를 읽음 (D)
• 노드 A -> 노드 B <- 노드 E : 노드 E에 대한 순회가 끝났으므로 노드 E의 이전 경로인 노드 B로 돌아감
• 노드 A <- 노드 B : 이로써 현재 노드 B에서 DLR 순회가 끝났으므로 다시 이전 노드 A로 돌아감

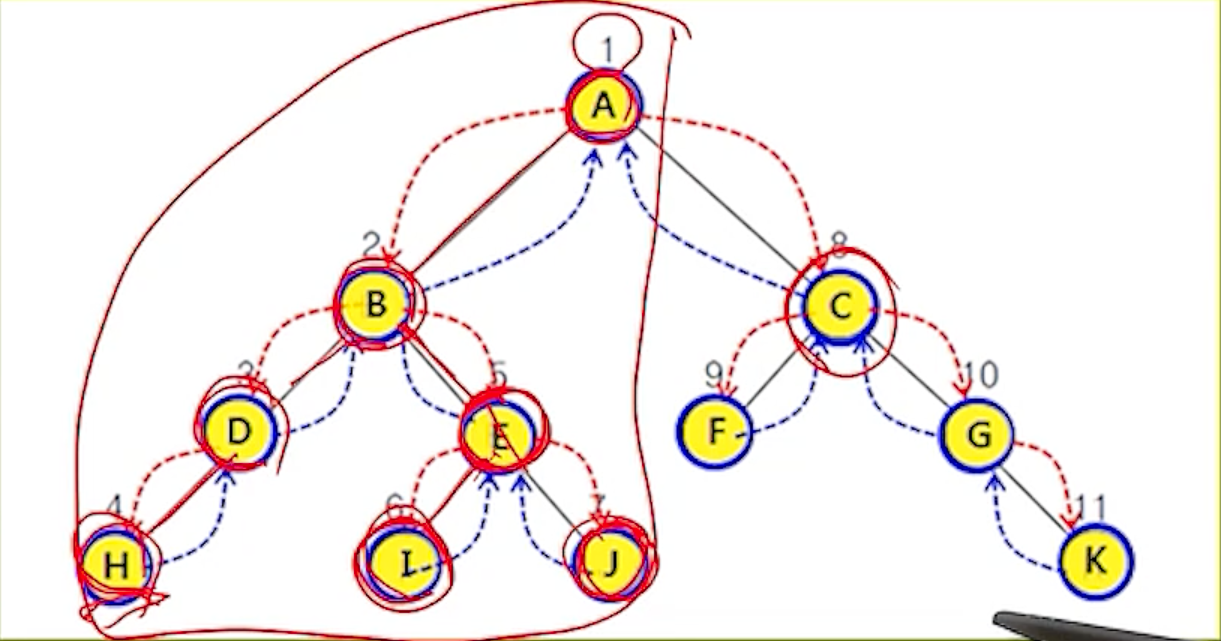
(4-8)

• 노드 A -> 노드 C : 현재 노드 A의 오른쪽 서브트리인 노드 C로 이동 (R)
• 노드 A -> 노드 C : 현재 노드 C의 데이터를 읽음 (D)

(4-9)

• 노드 A -> 노드 C -> 노드 F : 현재 노드 C의 왼쪽 단말 노드 F로 이동하여 데이터 읽음 (L)(D)
• 노드 A -> 노드 C -> 노드 G : 오른쪽 서브트리인 노드 G로 이동 (R)

(4-10)

• 노드 A -> 노드 C -> 노드 G : 현재 노드 G의 데이터를 읽음 (D)

(4-11)

• 노드 A -> 노드 C -> 노드 G -> 공백노드 : 노드 G의 왼쪽 노드인 공백 노드를 읽음 (D)
• 노드 A -> 노드 C -> 노드 G -> 노드 K : 노드 G의 오른쪽 단말 노드 k의 데이터를 읽음 (D)
• 이로서 루트 노드 A에 대한 DLR 순회가 끝났으므로 트리 전체에 대한 전위 순회가 완성

2) 중위 순회

(1) 수행방법

• 현재 노드 n의 왼쪽 서브트리로 이동 : L
• 현재 노드 n을 방문하여 처리 : D
• 현재 노드 n으 오른쪽 서브트리로 이동 : R

(2) 알고리즘

    inorder(T)
          if(T !=null) then{
                inorder(T.left);
                visit T.data;
                inorder(T.right);
          }
    end inorder()

(3) 예

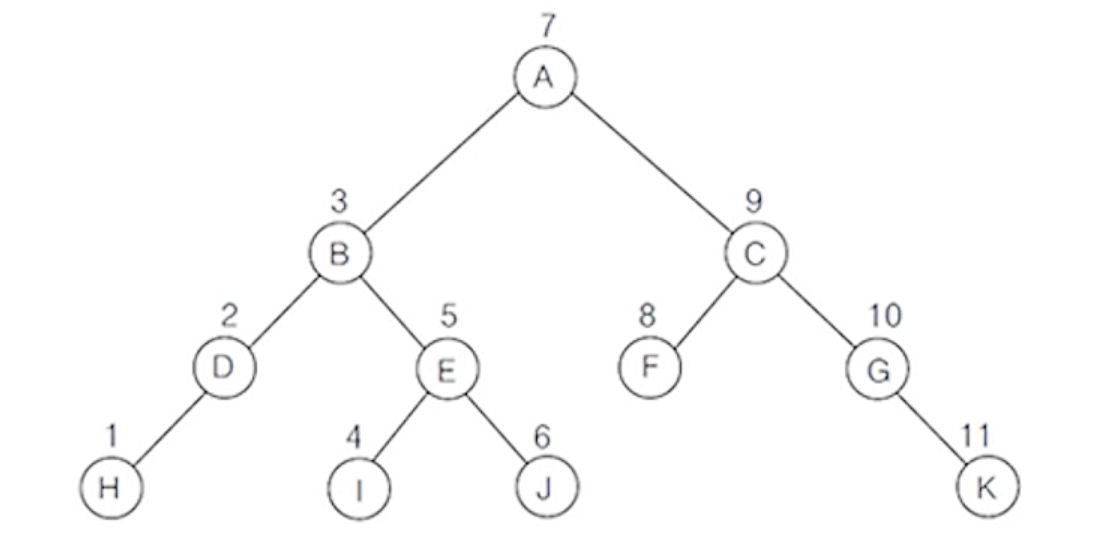
(4) 순회 과정 » H - D - B - I - E - J - A - F - C - G - K

(4-1)

• 노드 A -> 노드 B : 루트 A에서 중위 순회를 시작하여 노드 A의 왼쪽 서브 트리 B로 이동함 (L)
• 노드 A -> 노드 B -> 노드 D : 현재 노드 B의 왼쪽 서브트리 D로 이동 (L)
• 노드 A -> 노드 B -> 노드 D -> 노드 H : 현재 노드 D의 왼쪽 단말 노드 H의 데이터를 읽음 (D)

(4-2)

• 노드 A -> 노드 B -> 노드 D : 현재 노드 D의 데이터를 읽음 (D)
• 노드 A -> 노드 B -> 노드 D -> 공백노드 : 노드 D의 오른쪽 단말 노드인 공백 노드를 읽음 (D)
• 노드 A -> 노드 B <- 노드 D : 노드 D에서의 DLR 순회가 끝났으므로 이전 경로인 노드 B로 돌아감

3) 후위 순회

(1) 수행 방법

• 현재 노드 n의 왼쪽 서브트리로 이동함 : L
• 현재 노드 n의 오른쪽 서브트리로 이동함 : R
• 현재 노드 n을 방문하여 처리함 : D

(2) 알고리즘

    postorder(T)
          if(T !=null) then{
                postorder(T.left);
                postorder(T.right);
                visit T.data;
          }
    end postorder()

(3) 예

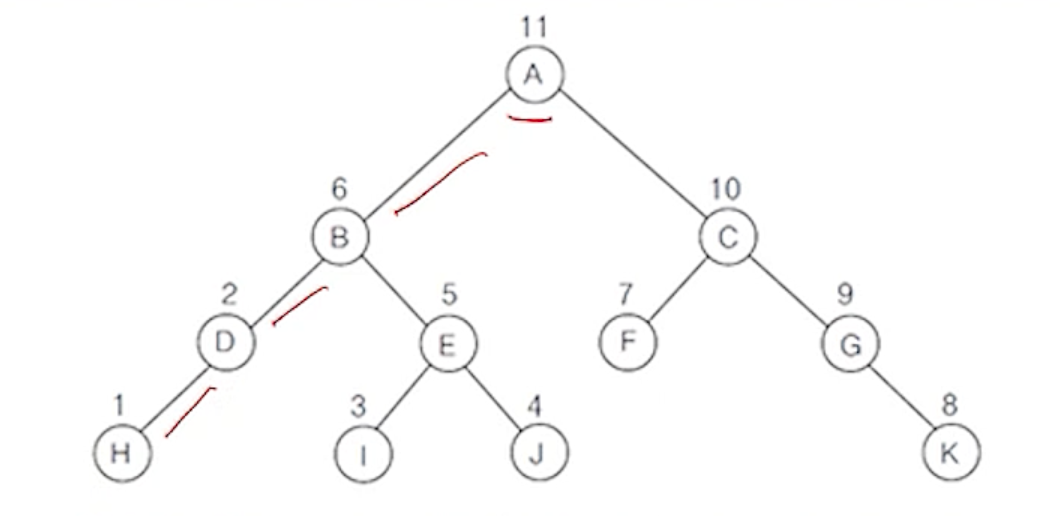
(4) 후위 순회 과정