자료 구조 - 이진 탐색 트리

1. 이진 탐색 트리의 탐색 연산

1) 이진 탐색 트리 (binary search tree)

• 이진 트리에 탐색을 위한 조건을 추가하여 정의한 자료구조

(1) 이진 탐색 트리의 정의

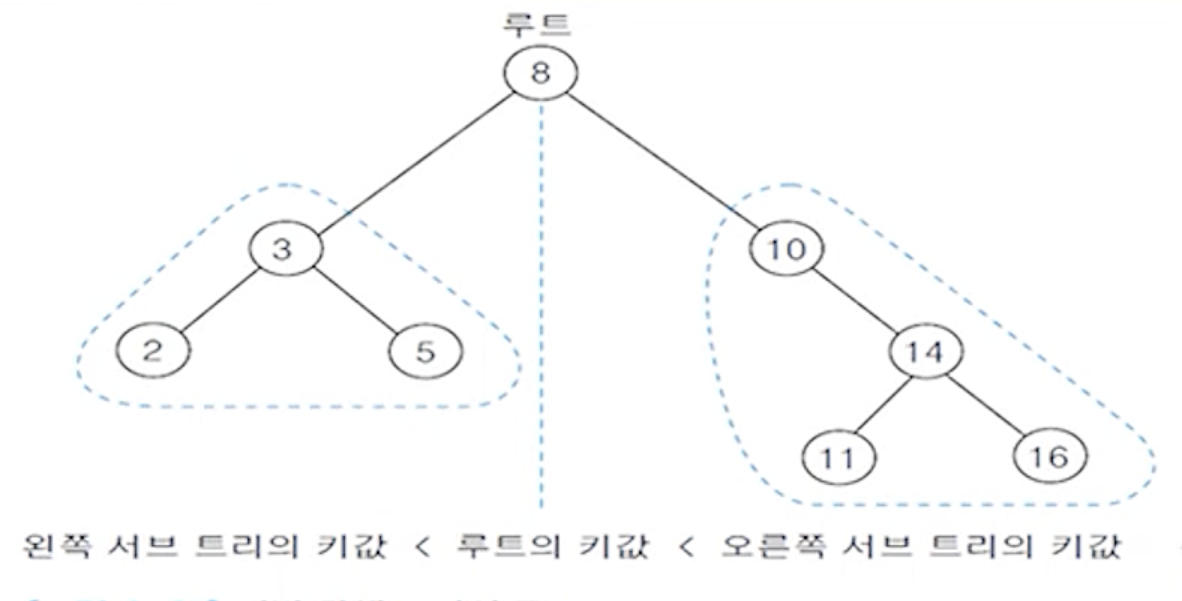
• 모든 원소는 서로 다른 유일한 키를 가짐
• 왼쪽 서브트리에 있는 원소의 키들은 그 루트의 키보다 작음
• 오른쪽 서브트리에 있는 원소들의 키들은 그 루트의 키보다 큼
• 왼쪽 서브트리와 오른쪽 서브트리도 이진 탐색 트리

2) 이진 탐색 트리의 탐색 연산

(1) 루트에서 시작함

(2) 탐색할 킷값 x를 루트 노드의 킷값과 비교함

• (킷값 x = 루트노드의 킷값)인 경우 : 원하는 원소를 찾았으므로 탐색연산 성공
• (킷값 x < 루트노드의 킷값)인 경우 : 루트노드의 왼족 서브트리에서 탐색연산 수행
• (킷값 x > 루트노드의 킷값)인 경우 : 루트노드의 오른쪽 서브트리에서 탐색연산 수행

3) 탐색 연산 알고리즘

• 이진 탐색 트리에서의 탐색 연산 알고리즘

      searchBST(bsT, x)
            p <- bsT;
            if (p = null) then
                  return null;
            if (x = p.key) then
                  return p;
            if (x < p.key) then
                  return searchBST(p.left, x);
            else return searchBST(p.right, x);

• 이진 탐색 트리에서의 탐색 과정

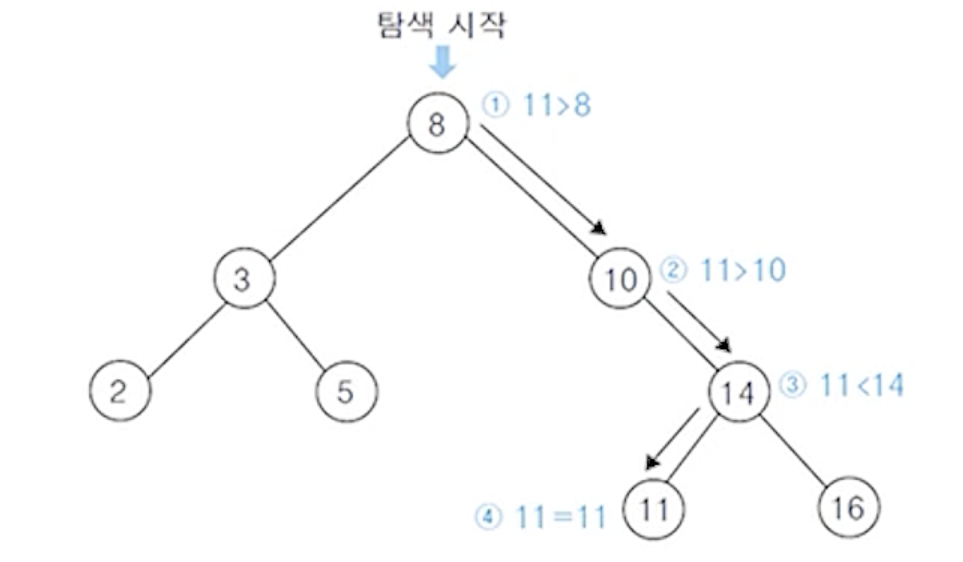
(1) 찾는 킷값 11을 루트노드의 킷값 8과 비교

• (찾는 킷값 11 > 노드의 킷값 8) 이므로 오른쪽 서브트리를 탐색

(2) (찾는 킷값 11 > 노드의 킷값 10)

• 다시 오른쪽 서브트리를 탐색

(3) (찾는 킷값 11 < 노드의 킷값 14)

• 왼쪽 서브트리를 탐색

(4) (찾는 킷값 11 < 노드의 킷값 11)

• 탐색 성공 ! (연산 종료)

2. 이진 탐색 트리의 삽입 연산

1) 이진 탐색 트리의 삽입 연산 절차

(1) 먼저 탐색 연산을 수행

• 삽입할 원소와 같은 원소가 트리에 있으면 삽입할 수 없으므로 같은 원소가 트리에 있는지 탐색하여 확인
• 탐색에서 탐색 실패가 결정되는 위치가 삽입 위치가 됨

(2) 탐색 실패한 위치에 원소를 삽입함

2) 삽입 연산 알고리즘

      insertBST(bsT, x)
            p <- bsT;
            while (p != null) do {
                  if (x = p.key) then return;
                  q <- p;                                   // (1) 삽입할 노드 탐색
                  if (x <p.key) then p <- p.left;
                  else p <- right;
            }

            new <- getNode();
            new.key <- x;
            new.left <- null;                               // (2) 삽입할 노드 생성
            new.right <- null;

            if( bsT = null) then bsT <- new;
            else if( x < q.key) then q.left <- new;
            else q.right <- new;                            // (3) 노드 연결
            return;
      end insertBST()

(1) 찾는 킷값 4를 루트노드의 킷값 8과 비교

• (찾는 킷값 4 < 노드의 킷값 8) 이므로, 왼쪽 서브트리를 탐색함

(2) (찾는 킷값 4 > 노드의 킷값 3)

• 오른쪽 서브트리를 탐색함

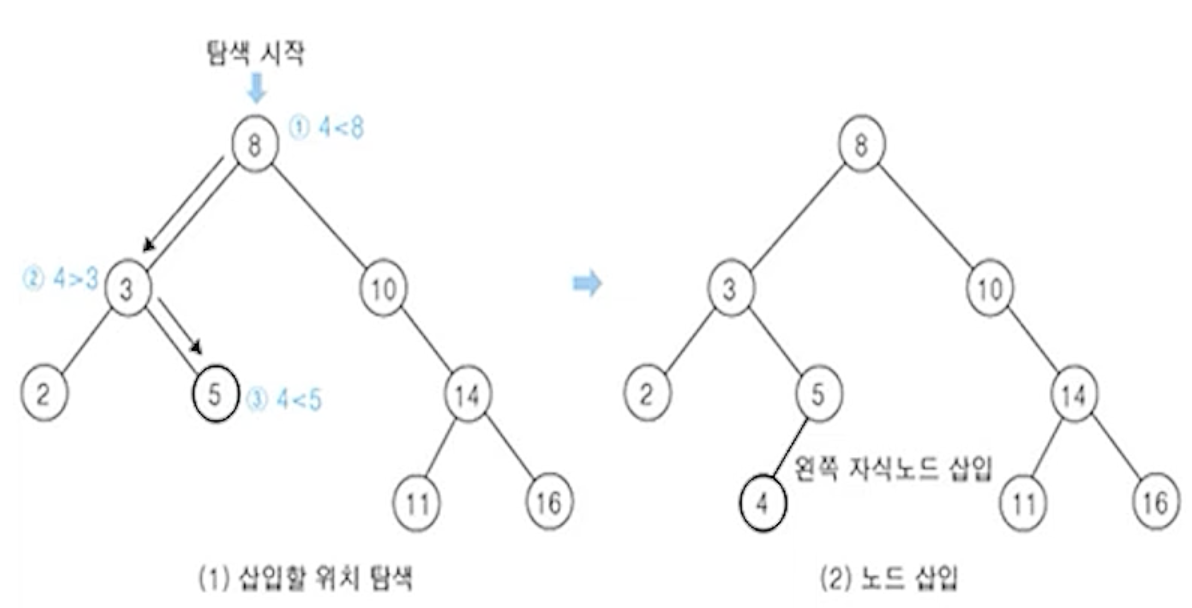
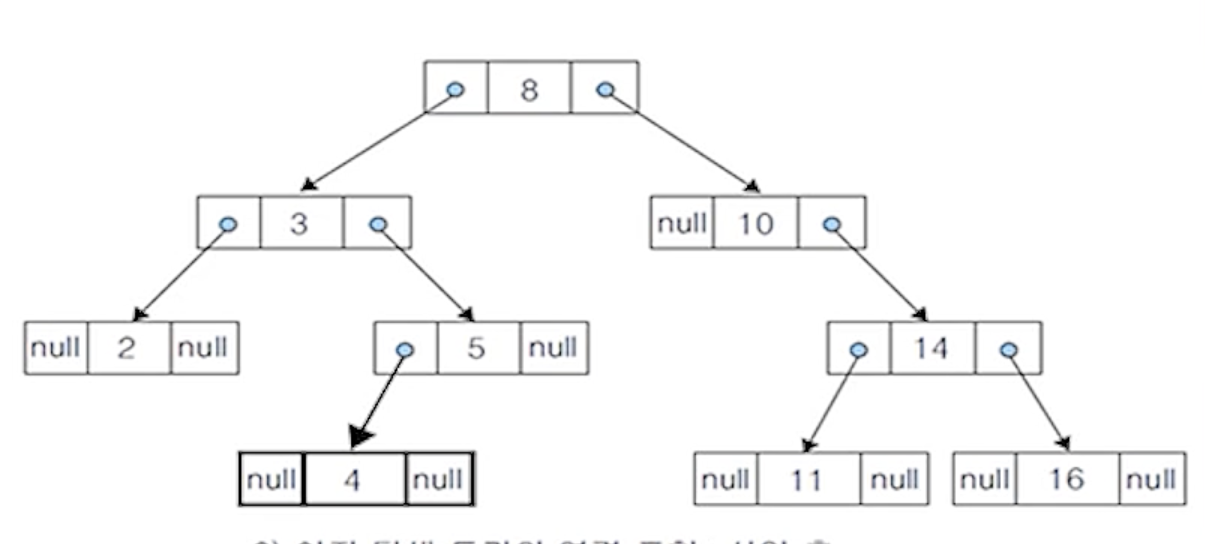
(3) 삽입 전

(4) 삽입 후

3. 이진 탐색 트리에 삭제 연산 절차

1. 먼저 탐색 연산을 수행
2. 탐색하여 찾은 노드를 삭제

1) 삭제 연산 절차

• 노드의 삭제 후에도 이진 탐색 트리를 유지해야 하므로 삭제 노드의 경우에 후속 처리가 필요함
• 이진 탐색 트리의 재구성 작업

(1) 삭제할 노드의 경우

• 삭제할 노드가 단말노드인 경우 : 차수가 0인 경우
• 삭제할 노드가 하나의 자식노드를 가진 경우 : 차수가 1인 경우
• 삭제할 노드가 두개의 자식노드를 가진 경우 : 차수가 2인 경우

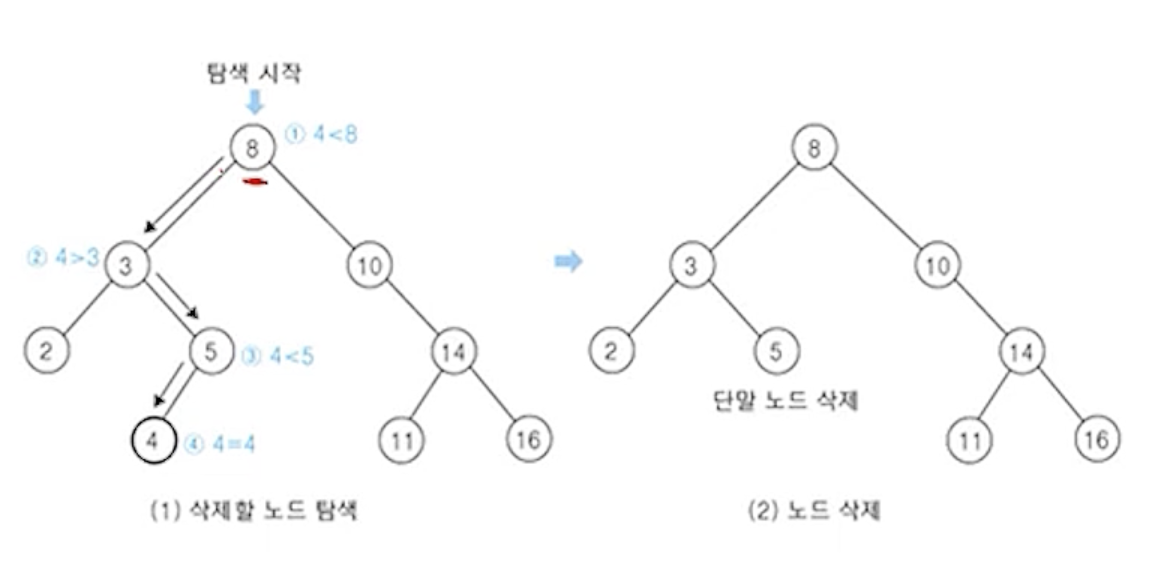
(2) 노드 4 삭제하기

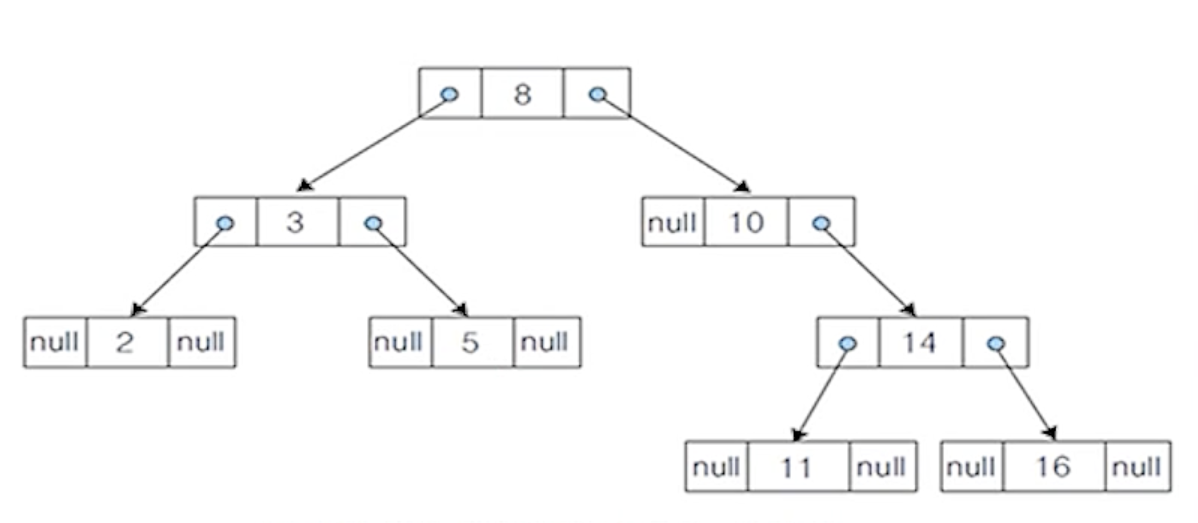
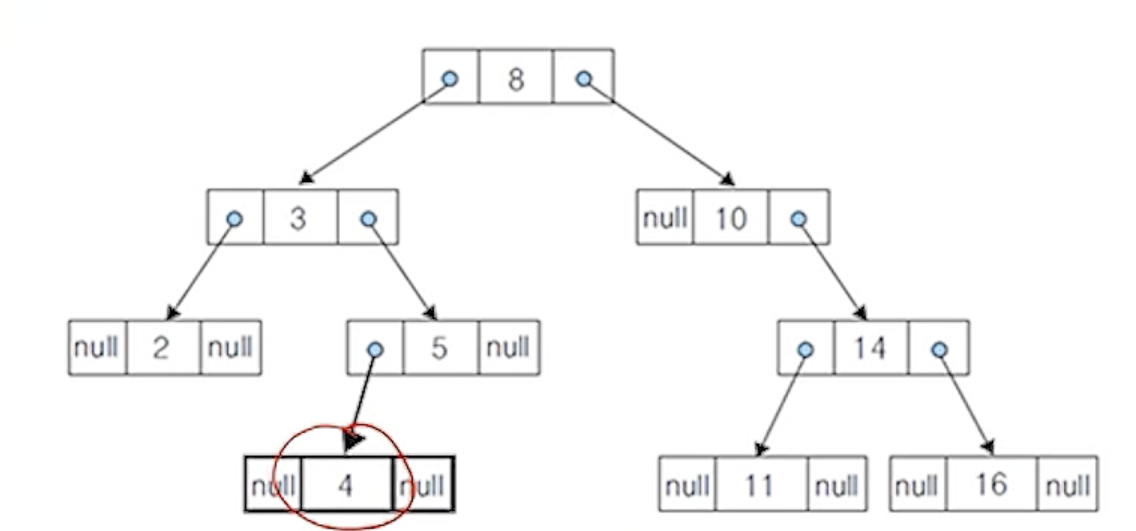
(3) 노드 4 삭제 - 단순 연결 리스트 표현 : 삭제 전

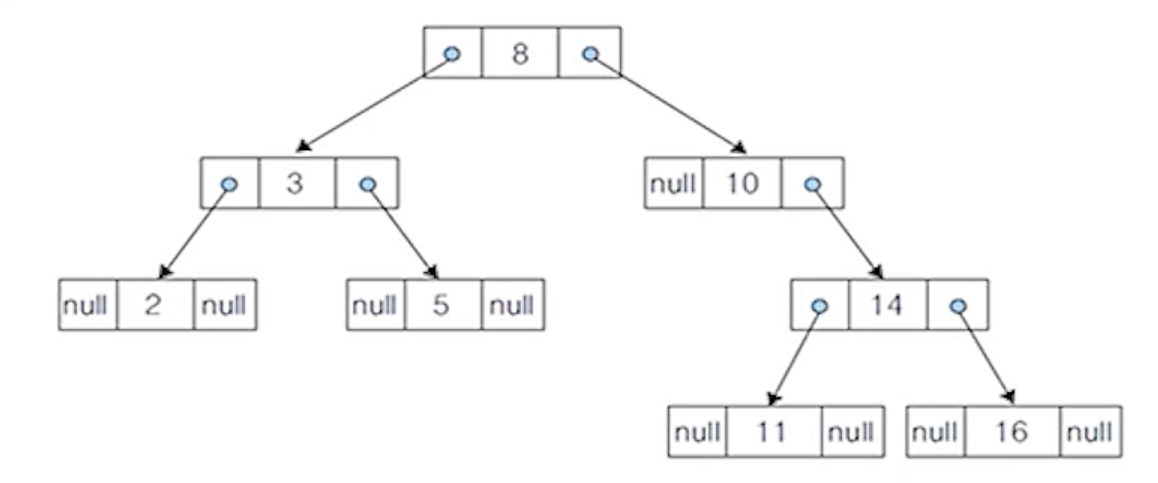
(4) 노드 4 삭제 - 단순 연결 리스트 표현 : 삭제 후

3) 삭제 연산 - 자식 노드가 하나인 노드 (차수 1노드 삭제)

• 노드를 삭제하면 자식 노드는 트리에서 연결이 끊어져 고아가 됨
• 후속 처리 : 이진 탐색 트리의 재구성
• 삭제한 부모노드의 자리를 자식노드에게 물려줌

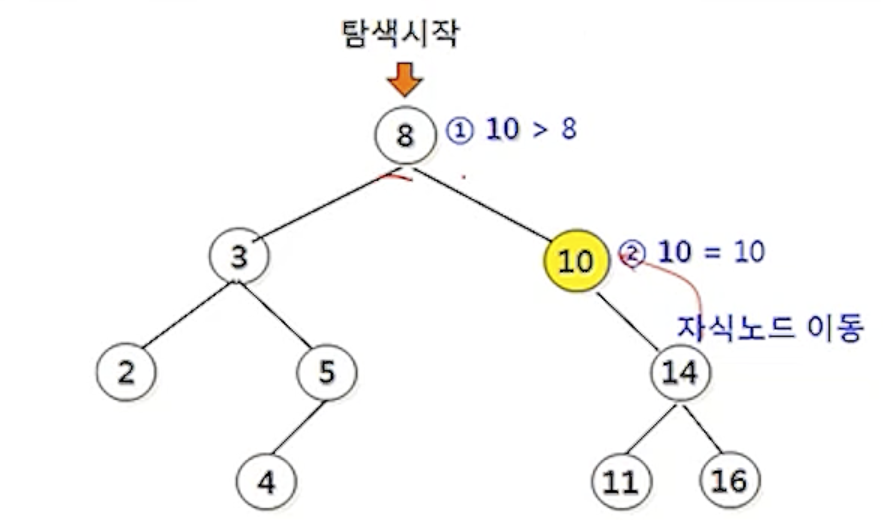
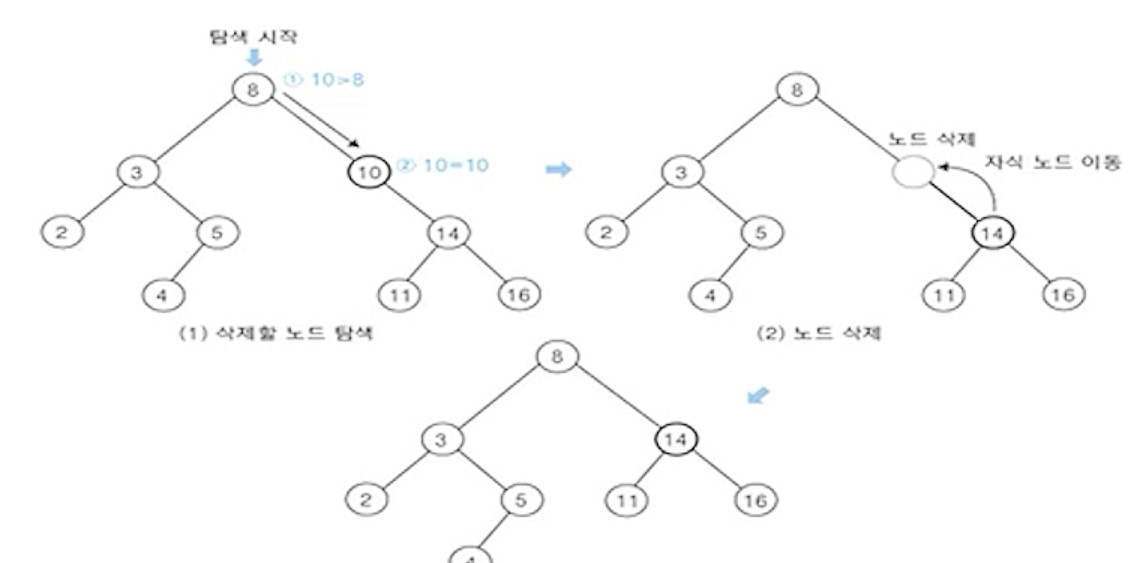
(1) 노드 10을 삭제하는 경우

• 1단계 : 삭제할 노드 탐색
• 2단계 : 탐색한 노드 삭제
• 3단계 : 후속 처리

• 위치 조정

4) 삭제 연산 - 자식 노드가 둘인 노드 (차수 2노드 삭제)

• 노드를 삭제하면 자식 노드들은 트리에서 연결이 끊어져 고아가 됨
• 후속처리 : 이진 탐색 트리의 재구성
• 삭제한 노드의 자리를 자손 노드들 중에서 선택한 후계자에게 물려줌

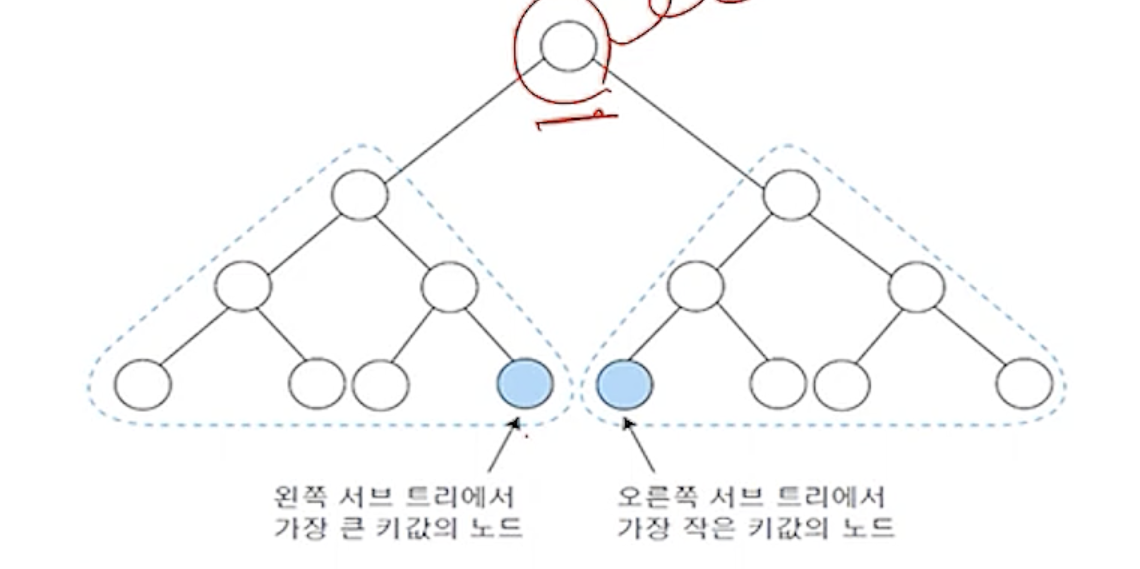
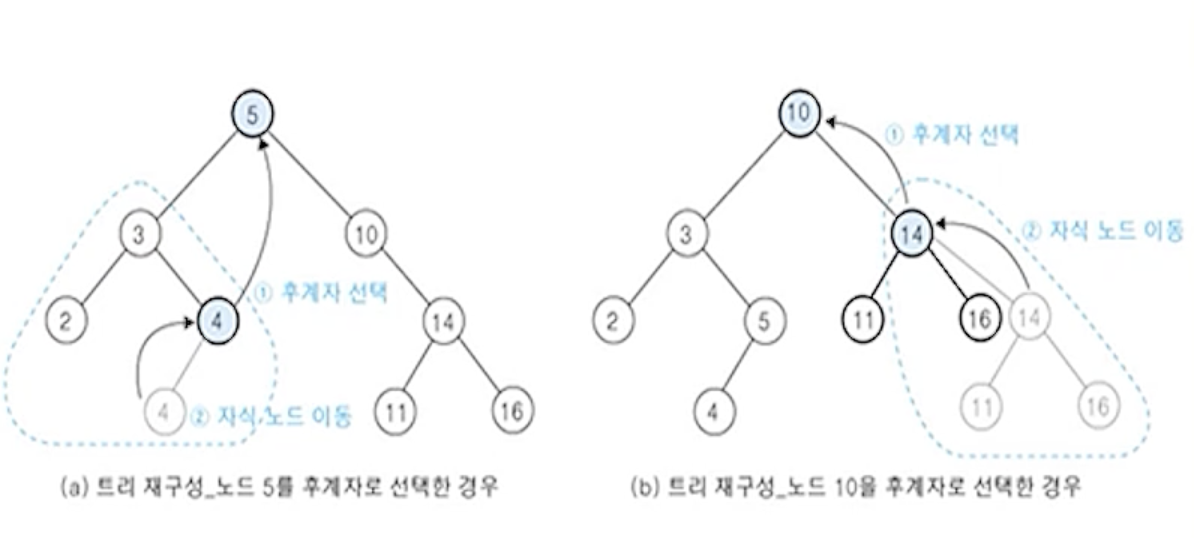
(1) 후계자 선택 - 방법 1

• 왼쪽 서브트리에서 가장 큰 자손노드 선택
• 왼쪽 서브트리의 오른쪽 링크를 따라 계속 이동하여 오른쪽 링크 필드가 null인 노드
• 즉, 가장 오른쪽에 있는 노드가 후계자가 됨

(2) 후계자 선택 - 방법 2

• 오른족 서브트리에서 가장 작은 자손노드 선택
• 오른쪽 서브트리에서 왼쪽 링크를 따라 계속 이동하여 왼쪽 링크 필드가 null인 노드
• 즉, 가장 왼쪽에 있는 노드가 후계자가 됨

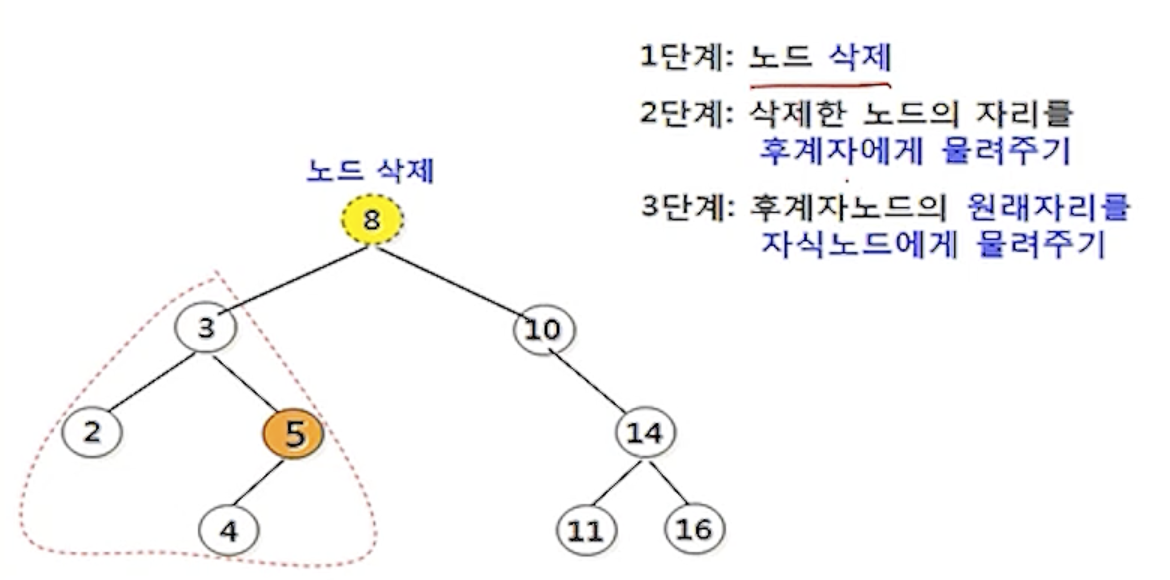
(3) 노드 8을 삭제하는 경우

• 후계자 선택

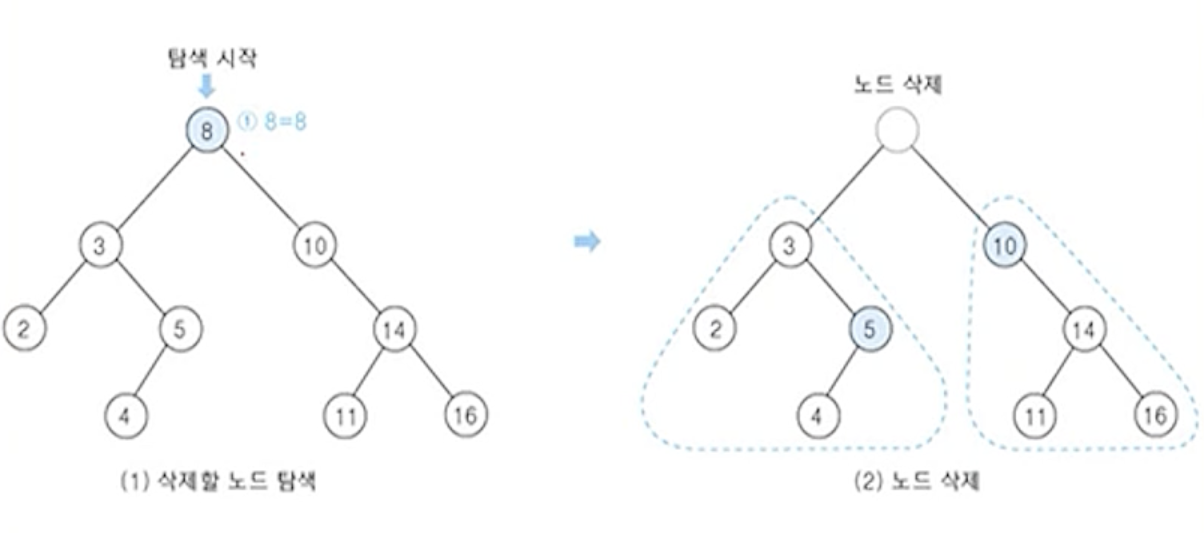
(4) 노드 5을 후계자로 선택한 경우

1. 후계자 노드 5를 원래자리에서 삭제하여, 삭제 노드 8의 자리를 물려줌
2. 후계자 노드 5의 원래자리는 자식노드 4에게 물려주어 이진 탐색트리를 재구성 함

• 자식 노드가 하나인 노드 삭제 연산의 후속처리 수행