자료 구조 - 히프

1. 히프와 히프의 추상 자료형

1) 히프 (Heap)

• 완전 이진 트리에 있는 노드 중에서 킷값이 가장 큰 도드나 킷값이 가장 작은 노드를 찾기 위해서 만든 자료구조

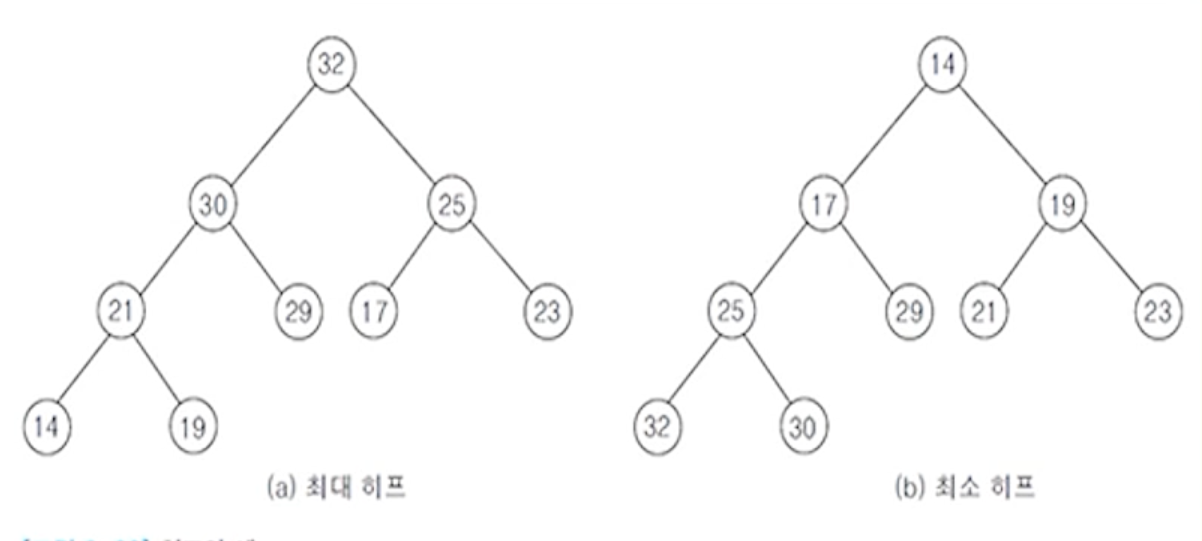
(1) 최대 히프

• 킷값이 가장 큰 노드를 찾기 위한 완전 이진트리
• 부모노드의 킷값 >= 자식 노드의 킷 값
• 루트 노드 : 킷값이 가장 큰 노드

(2) 최소 히프

• 킷값이 가장 작은 노드를 찾기 위한 완전 이진 트리
• 부모노드의 킷값 <= 자식 노드의 킷값
• 루트 노드 : 킷값이 가장 작은 노드

(3) 예

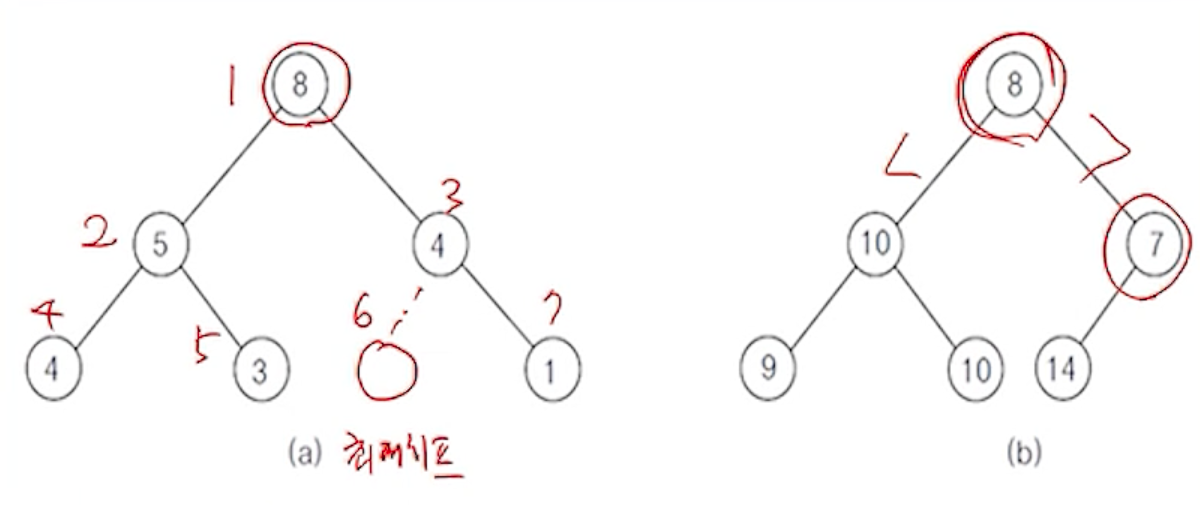
(3) 히프가 아닌 예

2. 히프의 삽입, 삭제 연산

1) 히프의 삽입 연산

(1) 완전 이진 트리를 유지하면서 확장한 노드에 삽입할 원소를 임시 저장

• 노드가 n개인 완전 이진 트리에서 다음 노드의 확장 자리는 n+1번의 노드가 됨
• n+1번 자리에 노드를 확장하고, 그 자리에 삽입할 원소를 임시 저장

(2) 만들어진 완전 이진 트리 내에서 삽입 원소의 제자리를 찾음

• 현재 위치에서 부모노드와 비교하여 크기 관계를 확인함
• (현재 부모노드의 킷값 >= 삽입 원소의 킷값)의 관계가 성립하지 않으면, 현재 부모노드의 원소와 삽입원소의
  자리를 서로 바꿈

2) 히프 연산 예제

(1) 예제 1 : 17을 삽입하는 경우

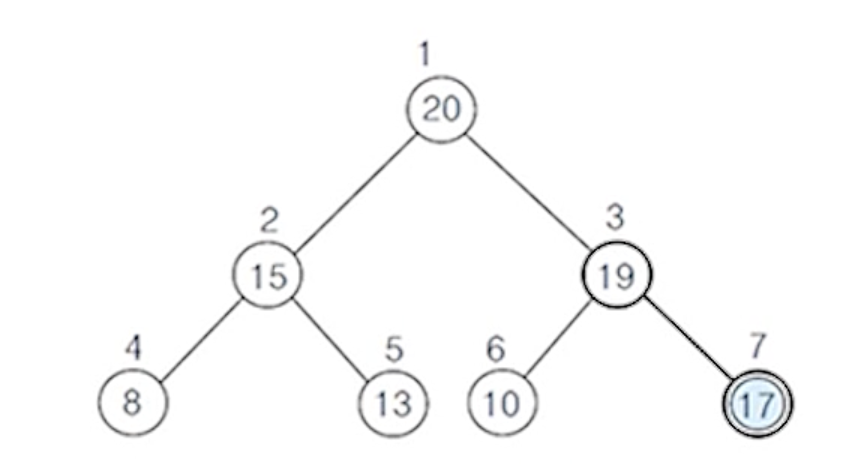
• 노드를 확장하여 임시로 저장한 위치에서의 부모 노드와 크기를 비교하여 히프의 크기 관계가 성립하므로
  현재 위치를 삽입 원소위 자리로 확정

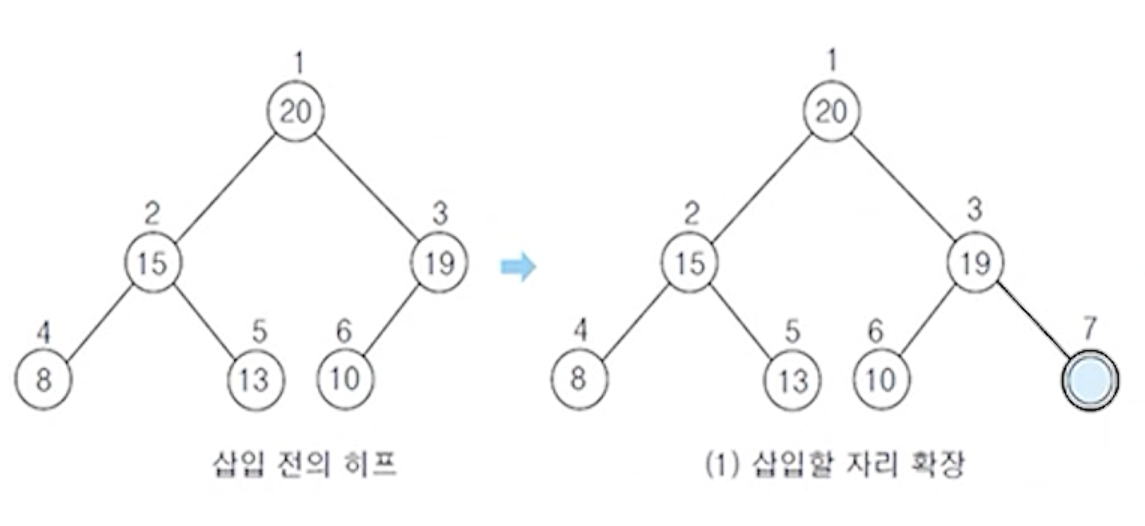
(1-1) 확장한 자리에 삽입할 원소 저장

(2) 예제 2 : 23을 삽입하는 경우

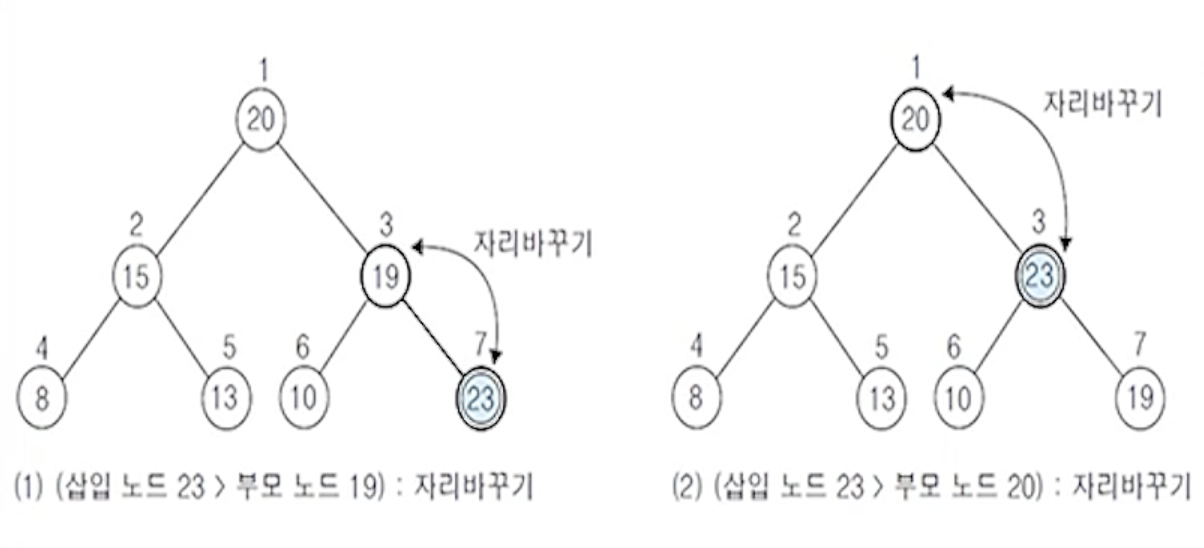
(2-1) 비교할 부모 노드가 없으므로 자리 확정

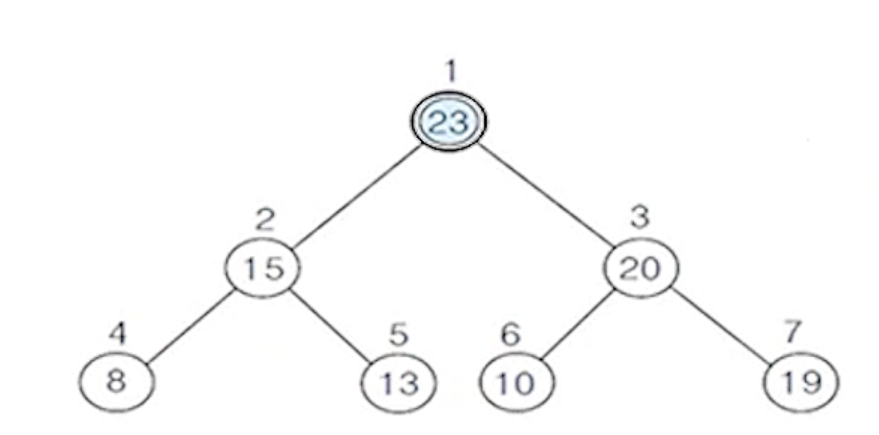
2) 히프에서의 삭제 연산

• 히프에서는 루트 노드의 원소만을 삭제할 수 있음

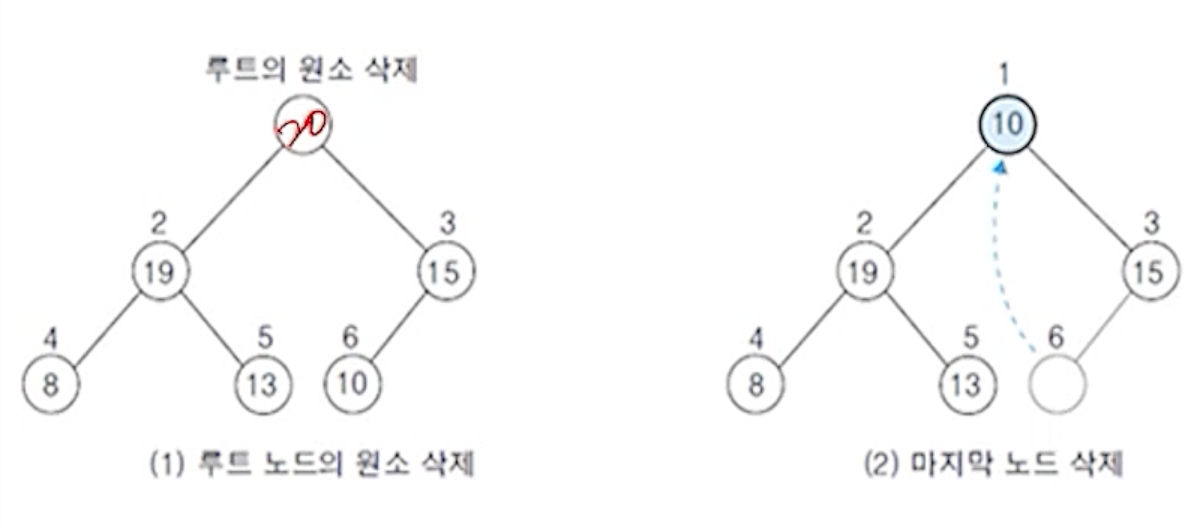
(1) 1단계

• 루트 노드의 원소를 삭제하여 반환함

(2) 2단계

• 원소의 개수가 n-1개로 줄었으므로, 노드의 수가 n-1인 완전 이진 트리로 조정
• 노드가 n개인 완전 이진 트리에서 노드 수 n-1개의 완전 이진 트리가 되기 위해서 마지막 노드, 즉 n번 노드를 삭제
• 삭제된 n번 노드에 있던 원소는 비어있는 루트노드에 임시 저장

(3) 3단계

• 완전 이진 트리 내에서 루트에 임시 저장된 원소의 제자리를 찾음
• 현재 위치에서 자식 노드와 비교하여 크기 관계를 확인함
• (임시 저장 원소의 킷값 >= 현재 자식노드의 킷값)의 관계가 성립하지 않으면, 현재 자식 노드의 원소와
  임시저장 원소의 자리를 서로 바꿈

3) 삭제 연산 예제

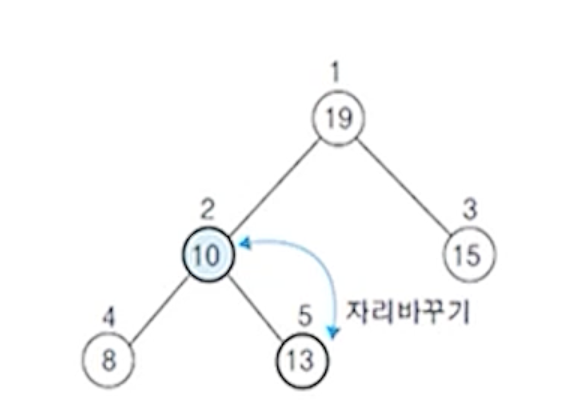
(1) (삽입 노드 10< 자식 노드 19) : 자리 바꾸기

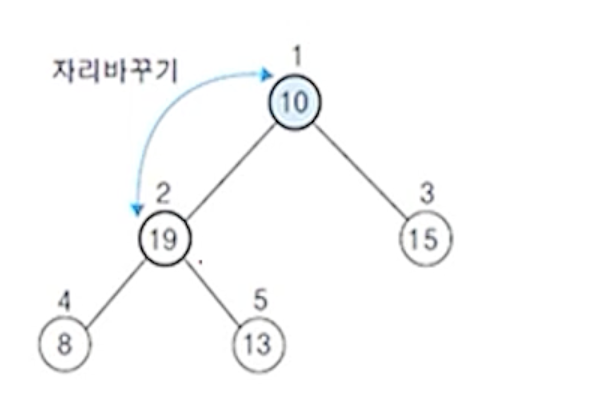
(2) (삽입 노드 10< 삽입 노드 13) : 자리 바꾸기

3. 순차 자료구조를 이용한 히프의 구현

1) 히프의 구현

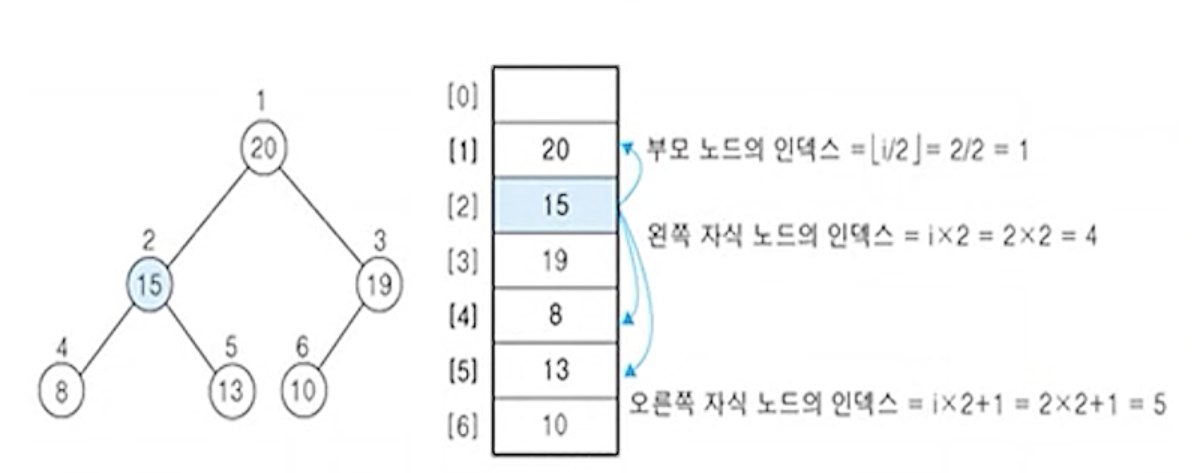
• 부모 노드와 자식 노드를 찾기 쉬운 1차원 배열의 순차 자료 구조 이용

(1) 1차원 배열을 이용한 히프의 표현 예