자료 구조 - 그래프의 구조와 구현

1. 그래프와 종류

1) 그래프

• 선형 자료구조나 트리 자료구조로 표현하기 어려운 다:다 관계를 가지는 원소들을 표현하기 위한 구조

(1) 그래프 G

• 객체를 나타내는 정점과 객체를 연결하는 간선의 집합

  G = (V,E)

• V는 그래프에 있는 정점들의 집합
• E는 정점을 연결하는 간선들의 집합

2) 그래프의 종류

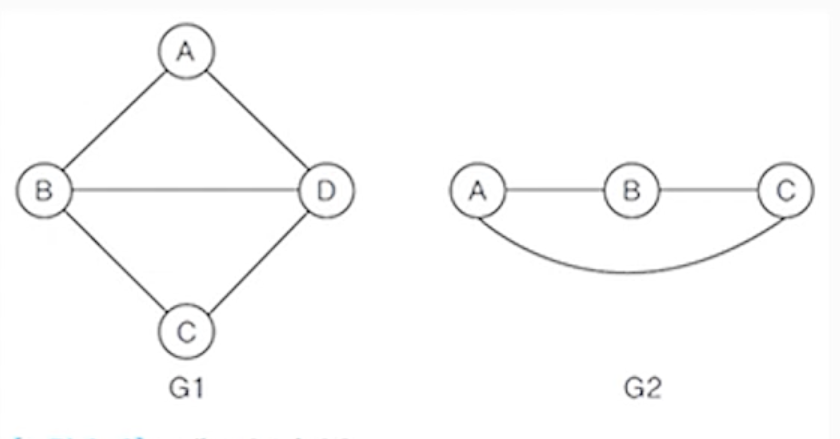
(1) 무방향 그래프 (undirected graph)

• 두 정점을 연결하는 간선의 방향이 없는 그래프
• 정점 Vi와 정점 Vj을 연결하는 간선을 (Vi, Vj)로 표현
• (Vi,Vj)와 (Vj,Vi)는 같은 간선을 의미함

  V(G1) = {A,B,C,D}
  E(G1) = {(A,B), (A,D), (B,C), (B,D), (C,D)}

  V(G2) = {A,B,C}
  E(G2) = {(A,B), (A,C), (B,C)}

• 그래프 G1과 G2

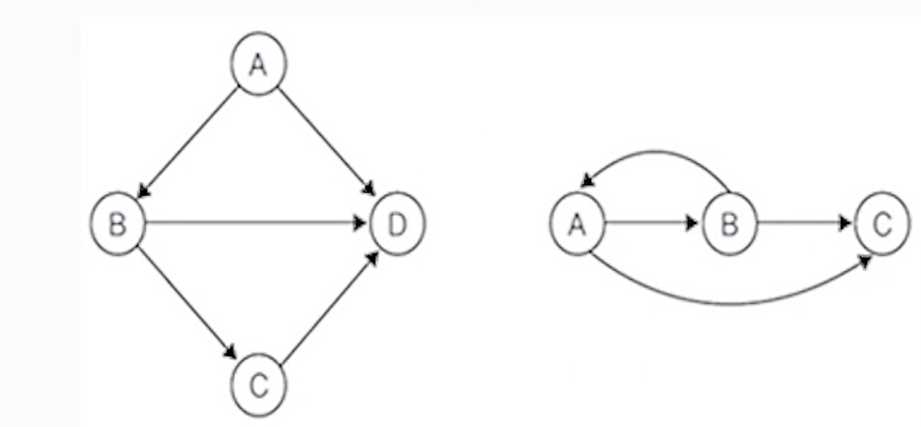
(2) 방향그래프, 다이그래프

• 간선이 방향을 가지고 있는 그래프
• 정점 Vi에서 정점 Vj를 연결하는 간선
• 즉, Vi -> Vj를 <Vi,Vj>로 표현
• Vi를 꼬리(tail), Vj를 머리(head)라고 함
• <Vi,Vj>와 <Vj,Vi>는 서로 다른 간선을 의미함

  V(G3) = {A,B,C,D}
  E(G3) = {<A,B>, <A,D>, <B,C>, <B,D>, <C,D>}

  V(G4) = {A,B,C}
  E(G4) = {<A,B>, <A,C>, <B,A>, <B,C>}

• 방향 그래프 G3, G4

(3) 완전 그래프 (complete graph)

• 각 정점에서 다른 모든 정점을 연결하여 가능한 최대의 간선 수를 가진 그래프
• 정점이 n개인 무방향 그래프에서 최대의 간선 수 : n(n-1)/2개
• 정점이 n개인 방향 그래프의 최대 간선 수 : n(n-1)개

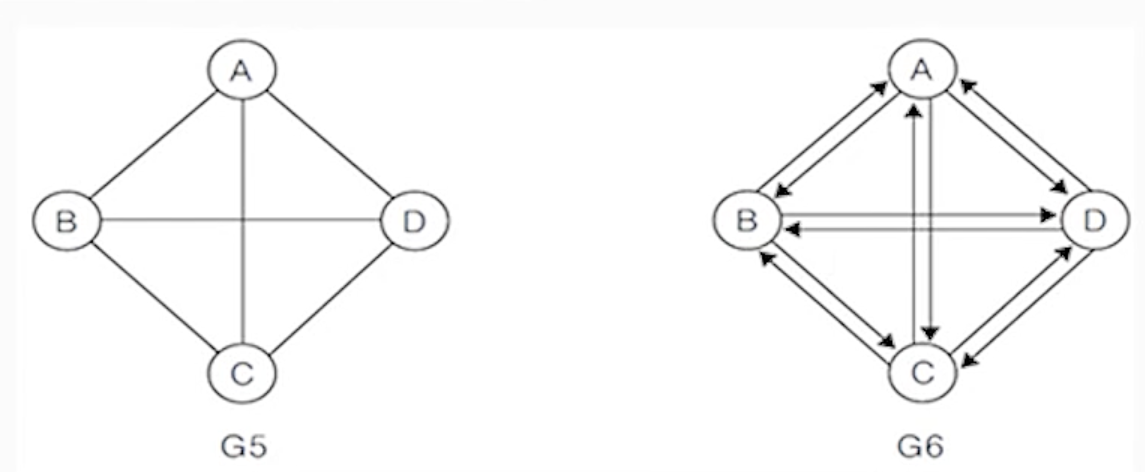
(3-1) 완전 그래프의 예

• G5는 정점의 개수가 4개인 무방향 그래프이므로 완전 그래프가 되려면 4(4-1)/2 = 6개의 간선 연결
• G6은 정점의 개수가 4개인 방향 그래프이므로 완전 그래프가 되려면 4(4-1) = 12개의 간선 연결

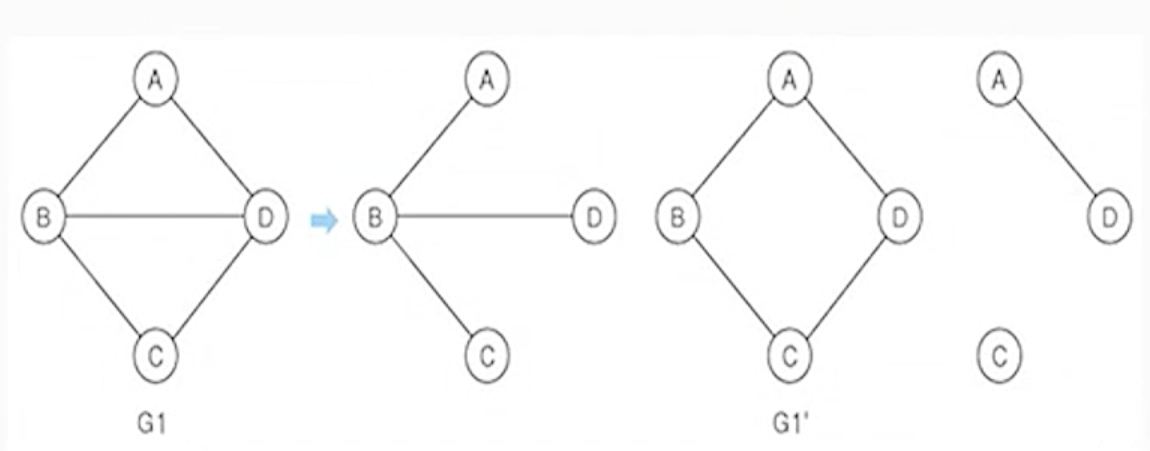
(4) 부분 그래프 (subgraph)

• 원래의 그래프에서 일부의 정점이나 간선을 제외하며 만든 그래프

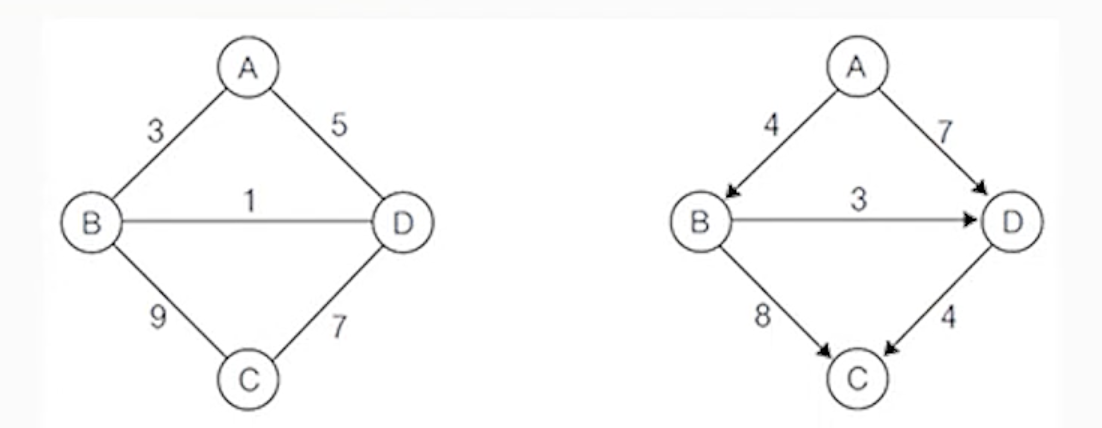
(5) 가중 그래프, 네트워크

• 정점을 연결하는 간선에 가중치를 할당한 그래프

3) 그래프 관련 용어

• 그래프에서 두 정점 Vi와 Vj를 연결하는 간선 (Vi,Vj)가 있을 때, 두정점 Vi와 Vj를 인접되어 있다고 함
• 간선 (Vi,Vj)는 정점 Vi와 Vj에 부속 되어있다고 함
• 그래프 G1에서 정점 A와 인접한 정점은 B와 D이고, 정점 A에 부속되어 있는 간선은 (A,B)와 (A,D)임

(1) 차수 (degree)

• 정점에 부속되어있는 간선의 수
• 무방향 그래프 G1에서 정점 A의 차수는 2, 정점 B의 차수는 3

(1-1) 방향 그래프의 정점의 차수 = 진입차수 + 진출차수

• 방향 그래프의 진입차수(in-degree) : 정점을 머리로 하는 간선의 수
• 방향 그래프의 진출차수(out-degree) : 정점을 꼬리로 하는 간선의 수
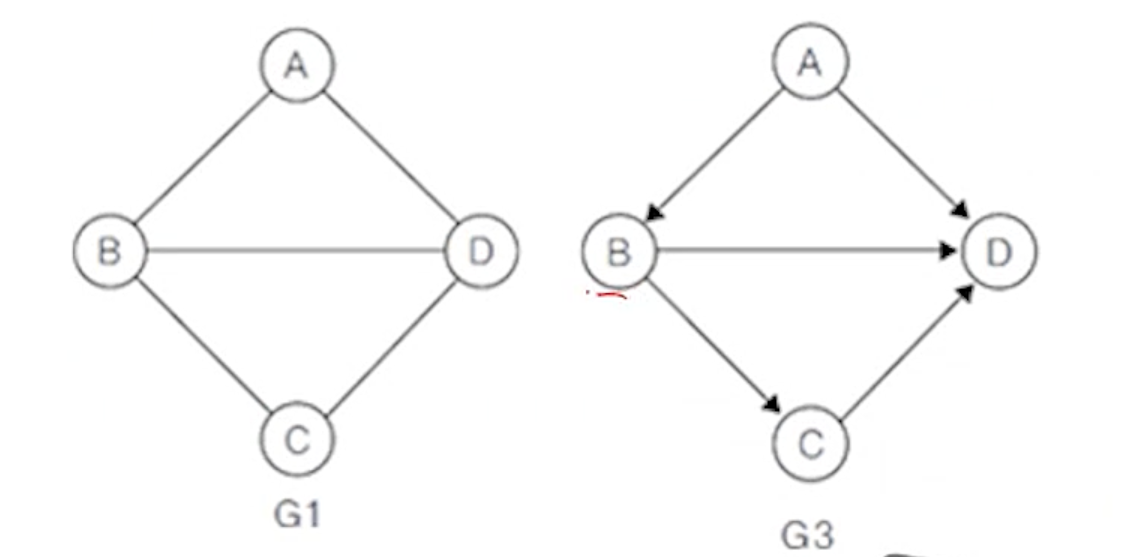
• 방향 그래프 G3에서 정점 B의 진입차수는 1, 진출 차수는 2
• 정점 B의 전체 차수는 (진입차수+진출차수) 이므로 3이 됨

(2) 경로

• 그래프에서 간선을 따라 갈수 있는 길을 순서대로 나열한 것
• 즉, 정점 Vi에서 Vj까지 간선으로 연결된 정점을 순서대로 나열한 리스트
• 그래프 G1에서 정점 A에서 정점 C까지는 A-B-C 경로와 A-B-D-C 경로, A-D-C 경로, 그리고 A-D-B-C 경로가 있음

(3) 경로 길이 (path length)

• 경로를 구성하는 간선의 수

(4) 단순 경로 (simple path)

• 모두 다른 정점으로 구성된 경로
• 그래프 G1에서 정점 A에서 정점 C까지의 경로 A-B-C는 단순 경로
• 경로 A-B-D-A-B-C는 단순 경로가 아님

(5) 사이클 (cycle)

• 단순 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로
• 그래프 G1에서 단순경로 A-B-C-D-A와 그래프 G4에서 단순경로 A-B-A는 사이클이 됨

(6) DAG (Diretecd acyclic graph)

• 방향 그래프이면서 사이클이 없는 그래프

(7) 연결 그래프 (connected graph)

• 서로 다른 모든 쌍의 정점들 사이에 경로가 있는 그래프
• 즉, 떨어져있는 정점이 없는 그래프
• 그래프에서 두 정점 Vi에서 Vj까지의 경로가 있으면 정점 Vi와 Vj가 연결되었다고 함

(8) 트리

• 사이클이 없는 연결 그래프