자료 구조 - 인접 행렬과 인접 리스트

1. 인접 행렬

1) 인접행렬의 정의

• 인접행렬은 행렬에 대한 2차원 배열을 사용하는 순차 자료구조 방법

(1) 그래프의 두정점을 연결한 간선의 유무를 행렬로 저장

• n개의 정점을 가진 그래프 : n x n 정방 행렬
• 행렬의 행번호와 열변호 : 그래프의 정점
• 행렬 값 : 두 정점이 인접되어있으면 1, 인접되어있지 않으면 0

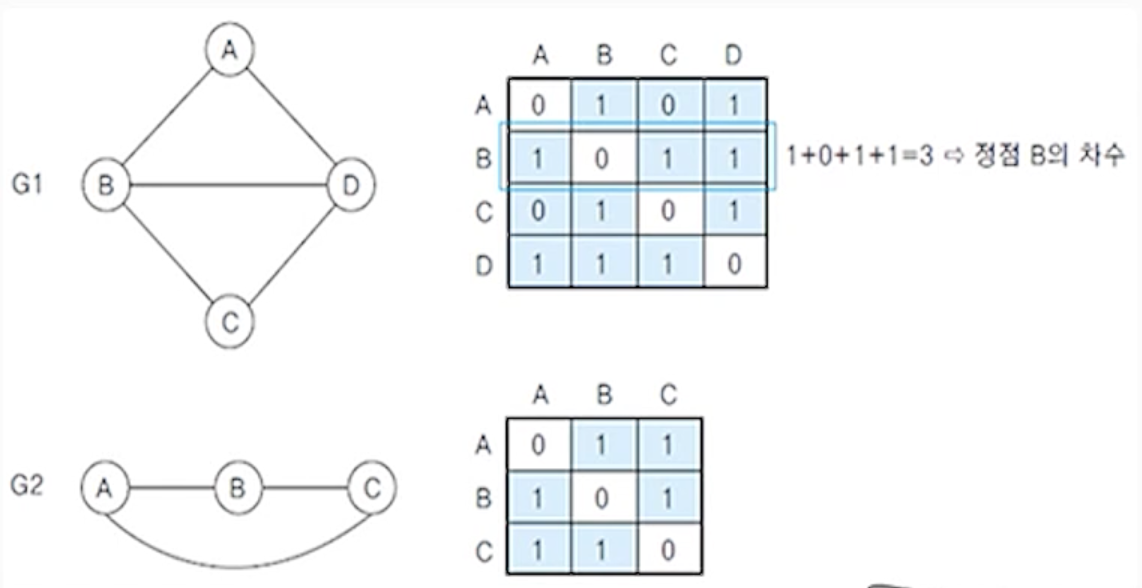
(2) 무방향 그래프의 인접 행렬

• 행 i의 합 = 열 i의 합 = 정점 i의 차수

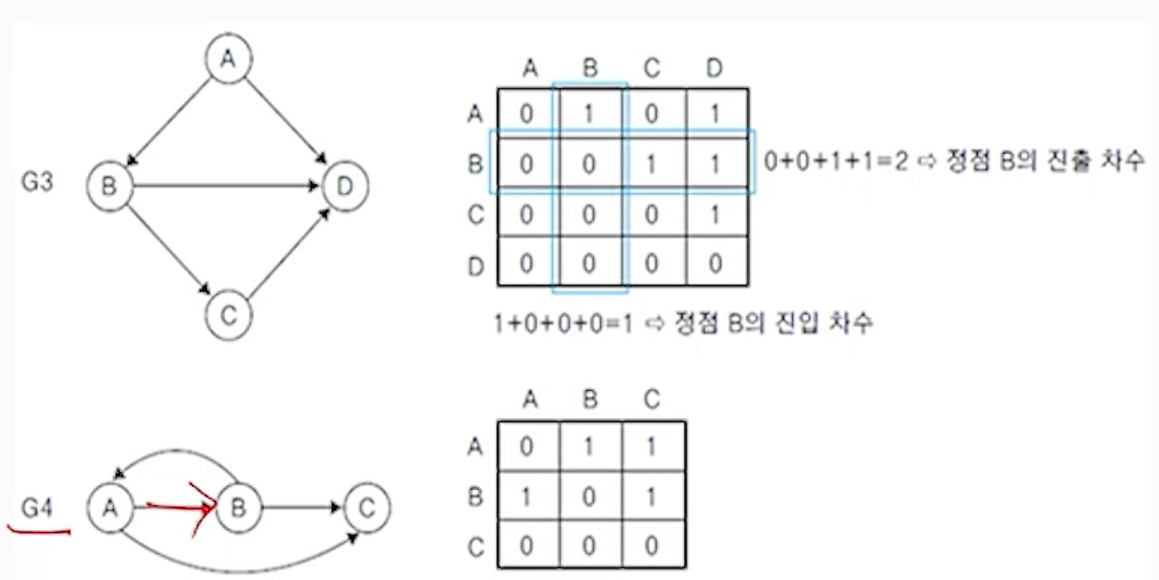
(3) 방향 그래프의 인접 행렬

• 행 i의 합 = 정점 i의 진출 차수
• 열 i의 합 = 정점 i의 진입 차수

(4) 그래프 G1,G2,G3,G4에 대한 인접행렬 표현

(5) 인접 행렬 표현의 단점

• n개의 정점을 가지는 그래프를 항상 n x n개의 메모리 사용
• 정점의 개수에 비해서 간선의 개수가 적은 희소 그래프에 대한 인접 행렬은 희소 행렬이 되므로 메모리의 낭비 발생

2. 인접 리스트

1) 정의

• 각 정점에 대한 인접 정점들을 연결하여 만든 단순 연결 리스트

(1) 각 정점의 차수만큼 노드를 연결

• 리스트 내의 노드들은 인접 정점에 대해서 오름차순으로 연결

(2) 인접 리스트의 각 노드

• 정점을 저장하는 필드와 다음 인접 정점을 연결하는 링크 필드로 구성

(3) 정점의 헤드 노드

• 정점에 대한 리스트의 시작을 표현

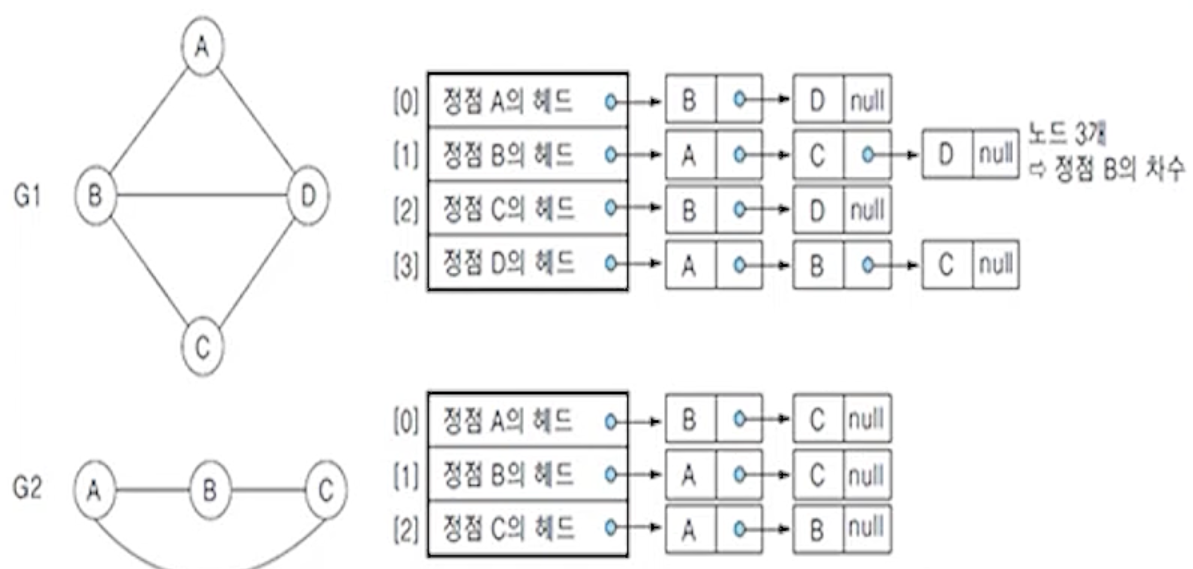
(4) n개의 정점과 e개의 간선을 가진 무방향 그래프의 인접 리스트

• 헤드 노드 배열의 크기 : n
• 연결하는 노드의 수 : 2e
• 각 정점의 헤드에 연결된 노드의 수 : 정점의 차수

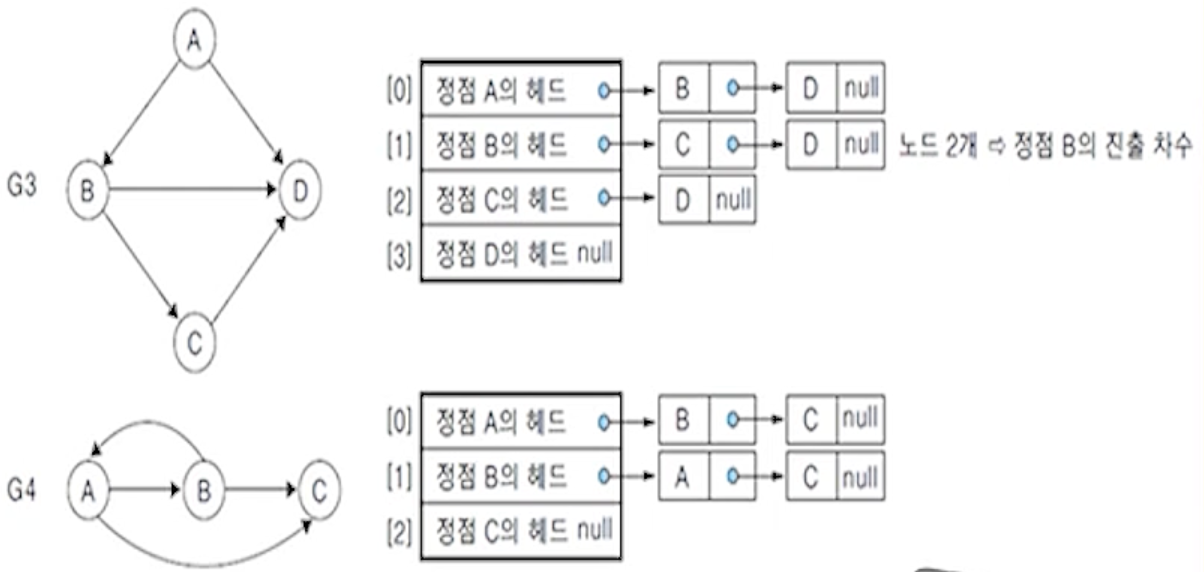
(4) n개의 정점과 e개의 간선을 가진 방향 그래프의 인접 리스트

• 헤드 노드 배열의 크기 : n
• 연결하는 노드의 수 : e
• 각 정점의 헤드에 연결된 노드의 수 : 정점의 진출 차수

(6) 그래프 G1,G2,G3,G4에 대한 인접 리스트