자료 구조 - Kruskal 알고리즘

1. Kruskal 알고리즘 1

• 가중치가 높은 간선을 제거하면서 최소 비용 신장 트리를 만드는 방법
• 그래프 G의 모든 간선을 가중치에 따라 내림차순으로 정리
• 그래프 G에서 가중치가 가장 높은 간선 제거
  • 이때 정점을 그래프에서 분리시키는 간선을 제거할 수 없으므로 이런 경우에는 그 다음으로 가중치가 높은 간선을 제거
• 그래프 G에 n-1개의 간선만 남을때까지 앞단계 반복
• 그래프에 n-1개의 간선이 남게 되면 최소 비용 신장 트리 완성

1) Kruskal 알고리즘 1의 이용

• Kruskal 알고리즘 1을 이용하여 G10의 최소 비용 신장 트리 만들기

(1) 초기상태 : 그래프 G 10의 간선을 가중치에 따라 내림차순으로 정렬

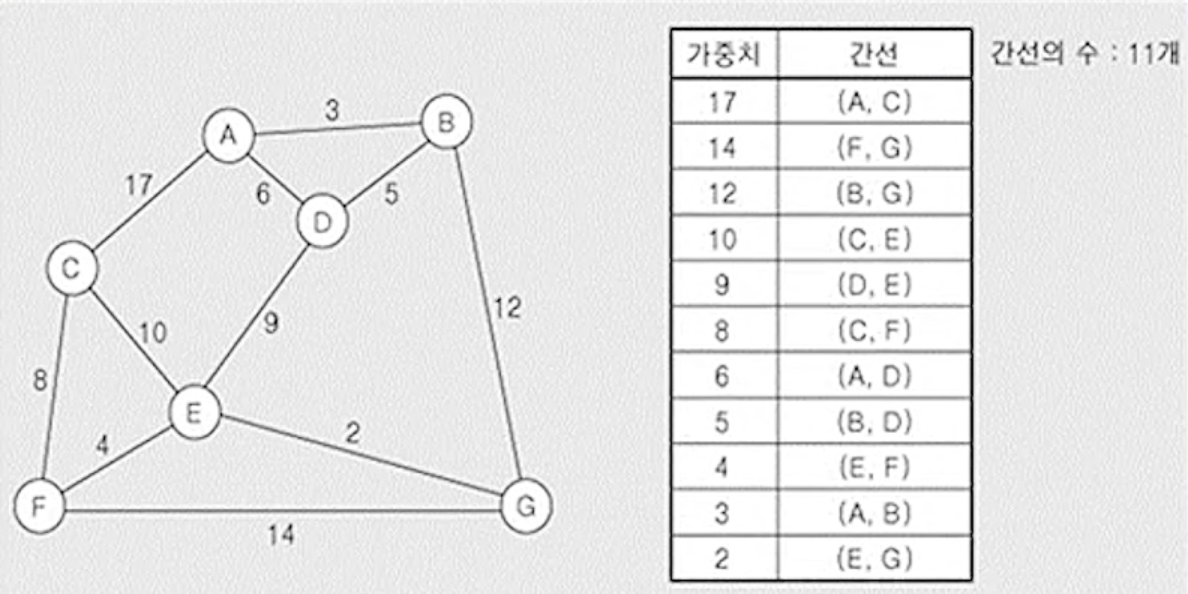
• 노드 7개
• 간선의 수 11개 ( 11개 -> 6개로 줄임 )

(2) 가중치가 가장 큰 간선 (A,C) 제거

• 현재 남은 간선의 수 : 10개

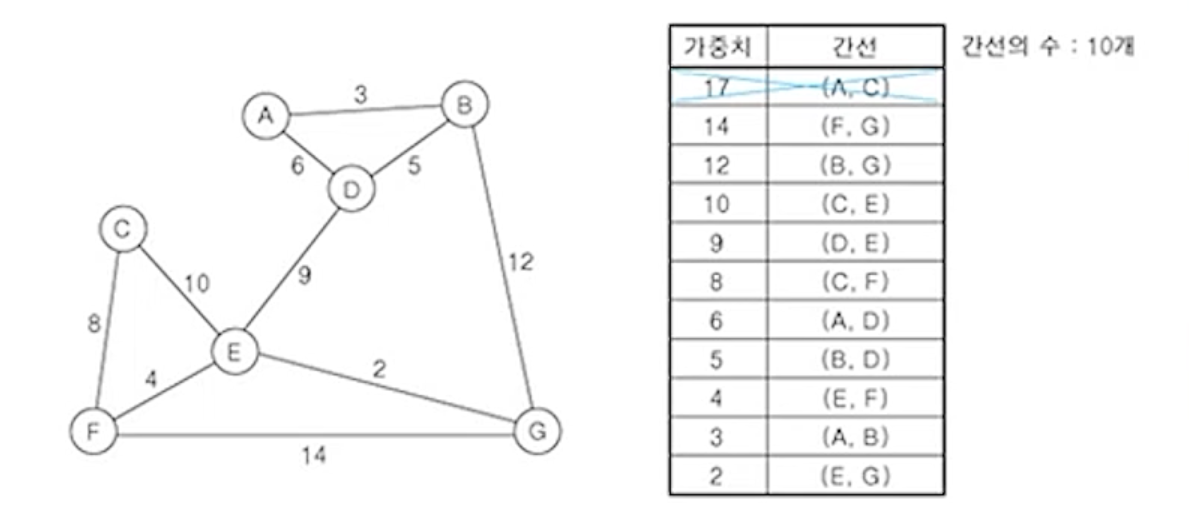
(3) 남은 간선 중에서 가중치가 가장 큰 간선 (F,G) 제거

• 현재 남은 간선의 수 : 9개

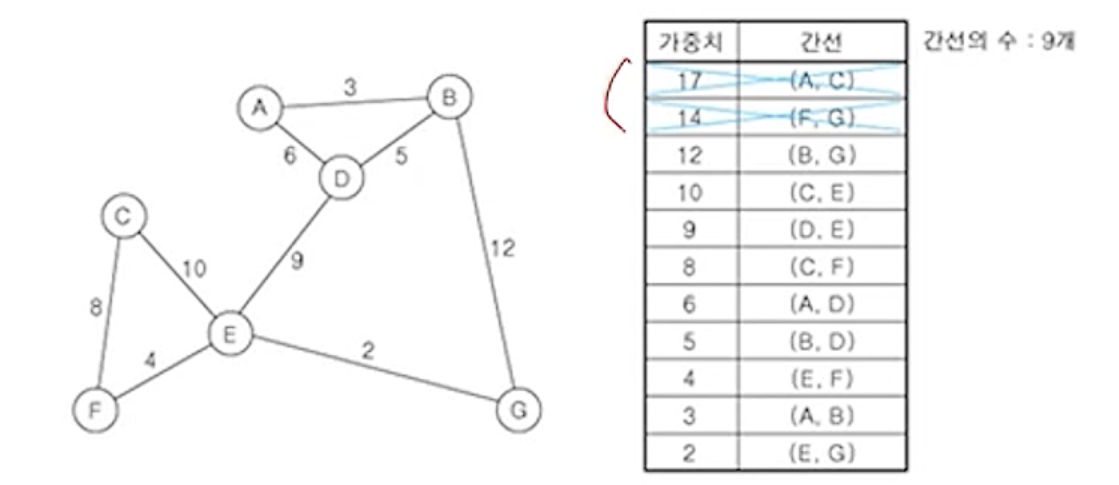
(4) 남은 간선 중에서 가중치가 가장 큰 간선 (B,G) 제거

• 현재 남은 간선의 수 : 8개

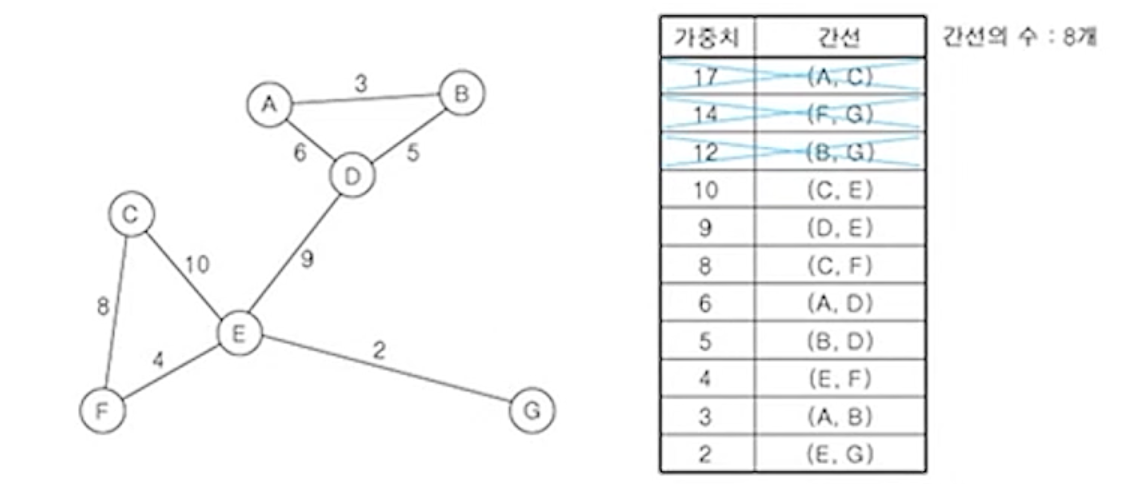
(5) 남은 간선 중에서 가중치가 가장 큰 간선 (C,E) 제거

• 현재 남은 간선의 수 : 7개

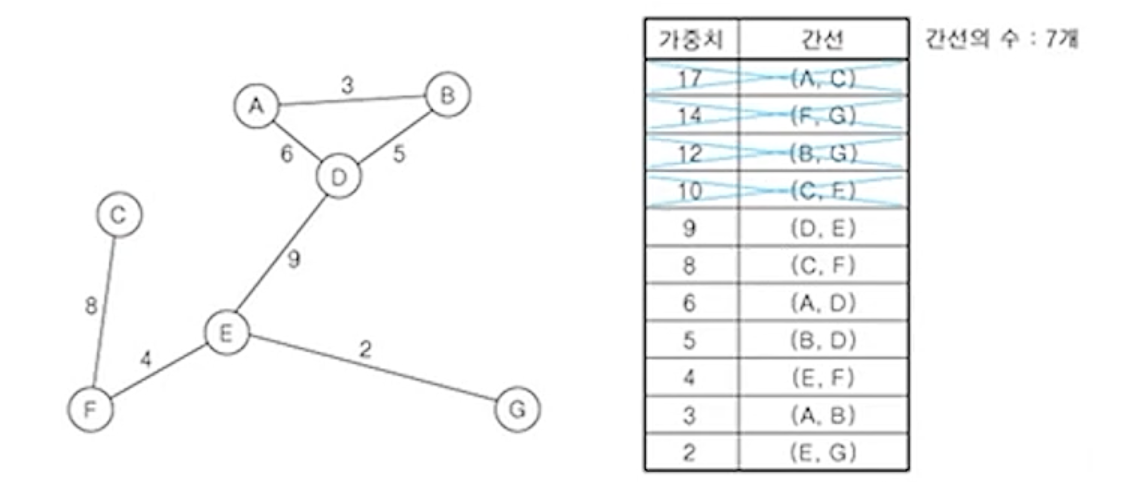
(6) 남은 간선 중에서 가중치가 가장 큰 간선 (D,E)를 제거하면

• 그래프가 분리되어 단절 그래프가 됨
• 그 다음으로 가장 큰 간선 (C,F)를 제거해야함
• 그런데 간선 (C,F)를 제거하면 정점 C가 분리되므로 제거할 수 없음
• 다시 그 다음 가중치가 큰 간선 (A,D)를 제거
• 현재 남은 간선의 수 : 6개

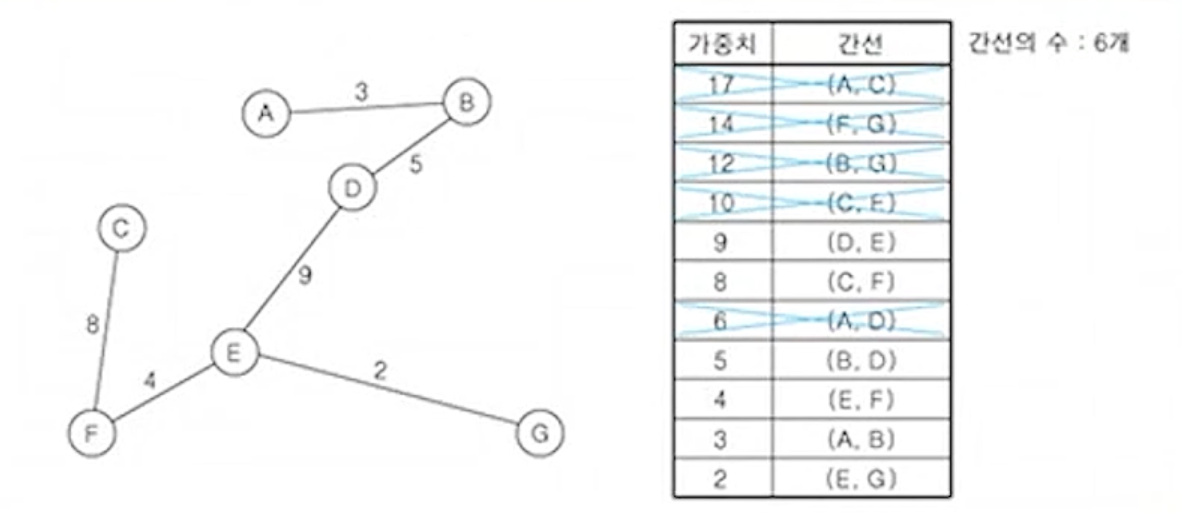
• 현재 남은 간선의 수가 6개 이므로 알고리즘 수행을 종료하고 신장 트리 완성

2. Kruskal 알고리즘 2

• 가중치가 낮은 간선을 삽입하면서 최소 비용 신장 트리를 만드는 방법
• 그래프 G의 모든 간선을 가중치에 따라 오름차순으로 정리
• 그래프 G에 가중치가 가장 작은 간선을 삽입
  • 이때 사이클을 형성하는 간선은 삽입할 수 없으므로 이런 경우에는 그 다음으로 가중치가 작은 간선을 삽입
• 그래프 G에 n-1개의 간선을 삽입할 때까지 앞 단계 반복
• 그래프 G의 간선이 n-1개가 되면 최소 비용 신장 트리가 완성

1) Kruskal 알고리즘 2의 이용

• Kruskal 알고리즘 2를 이용하여 G10의 최소 비용 신장 트리 만들기

(1) 초기 상태 : 그래프 G10의 간선을 가중치에 따라서 오름차순 정렬

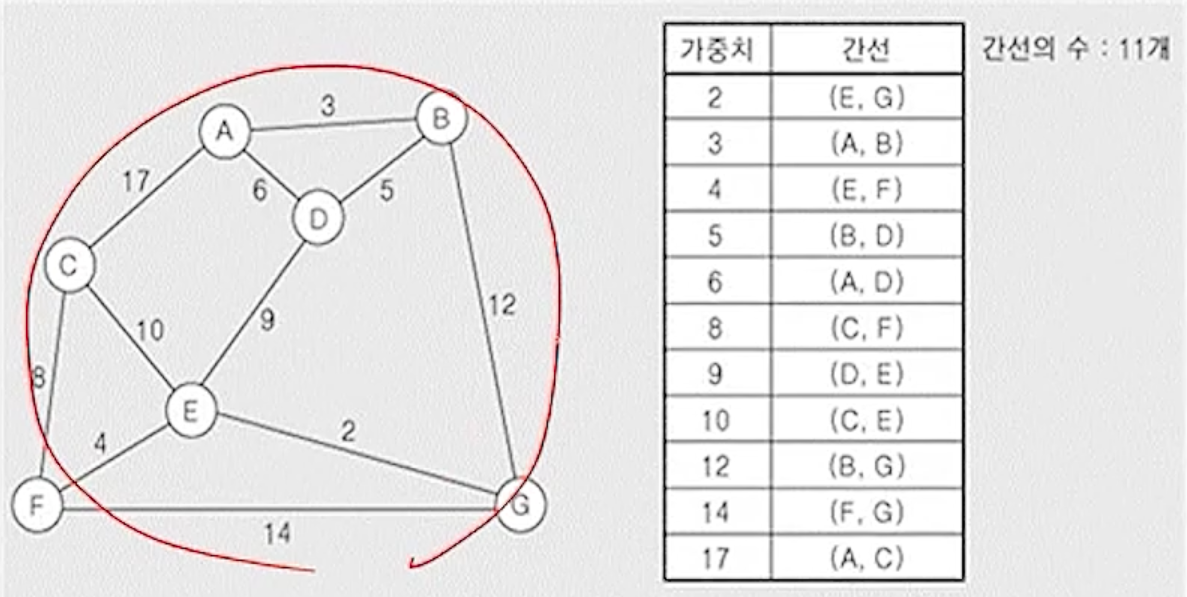
(2) 나머지 가중치가 가장 작은 간선 (E,G) 삽입

• 현재 삽입한 간선의 수 : 1개

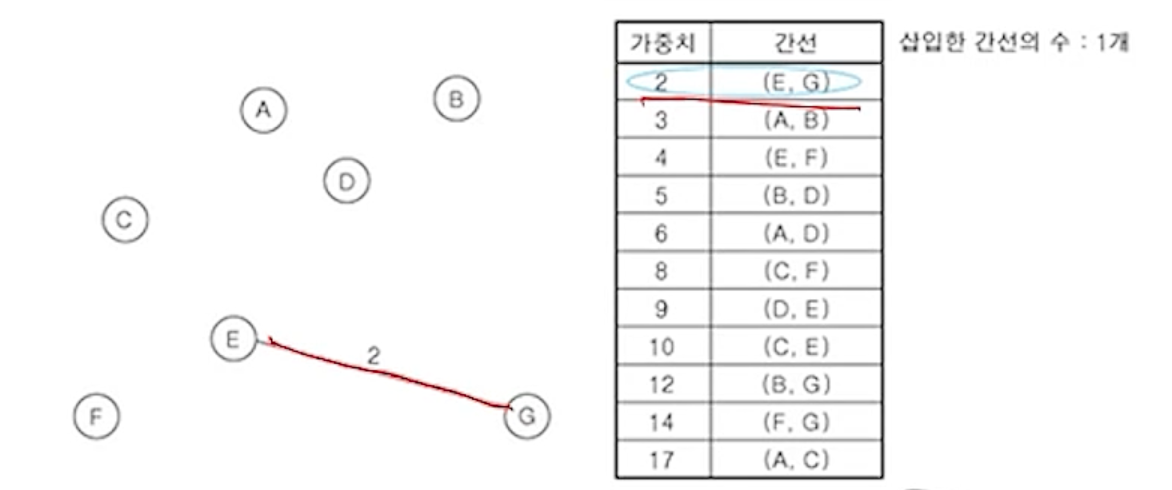
(3) 나머지 간선 중에서 나머지 가중치가 가장 작은 간선 (A,B) 삽입

• 현재 삽입한 간선의 수 : 2개

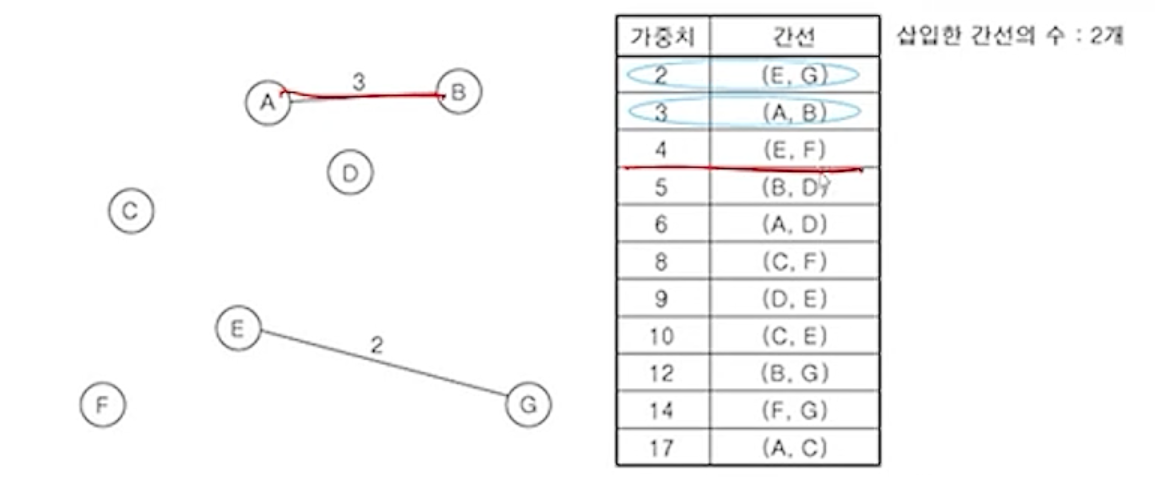
(4) 나머지 간선 중에서 나머지 가중치가 가장 작은 간선 (E,F) 삽입

• 현재 삽입한 간선의 수 : 3개

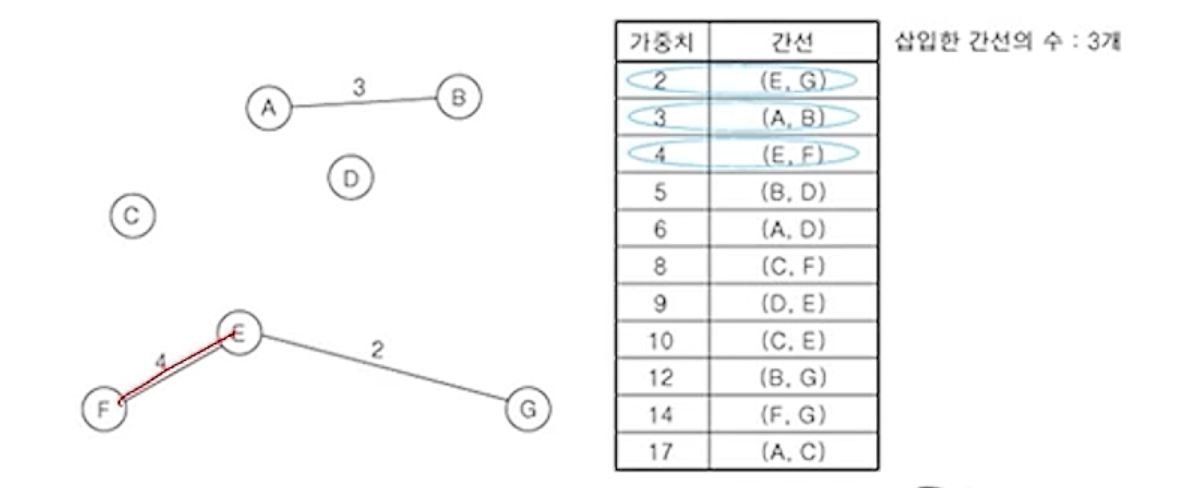
(5) 나머지 간선 중에서 나머지 가중치가 가장 작은 간선 (B,D) 삽입

• 현재 삽입한 간선의 수 : 4개

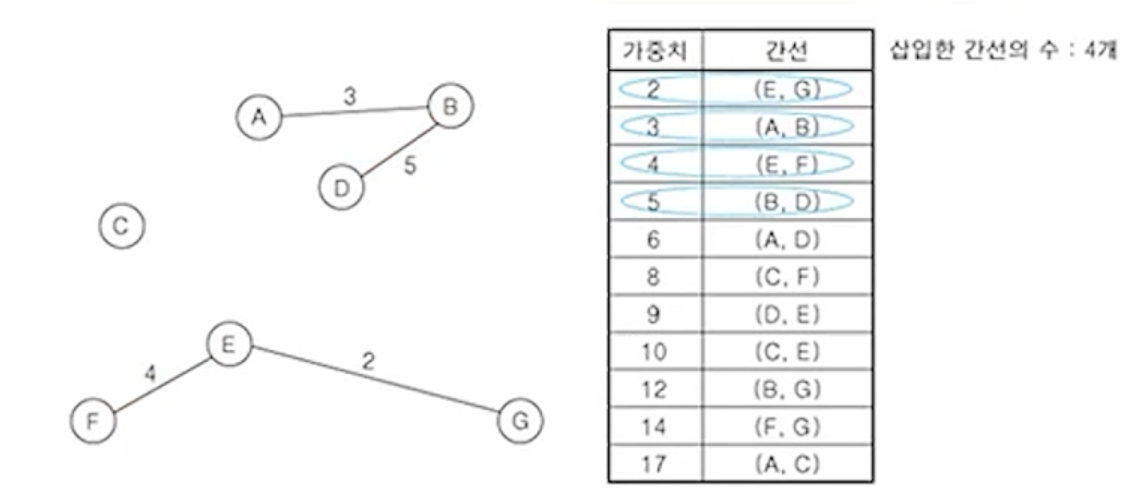
(6) 나머지 간선 중에서 나머지 가중치가 가장 작은 간선 (A,D) 삽입

• A-B-D의 사이클이 생성되므로 삽입 할수 없음
• 그 다음으로 가중치가 가장 작은 간선 (C,F) 삽입
• 현재 삽입한 간선의 수 : 5개

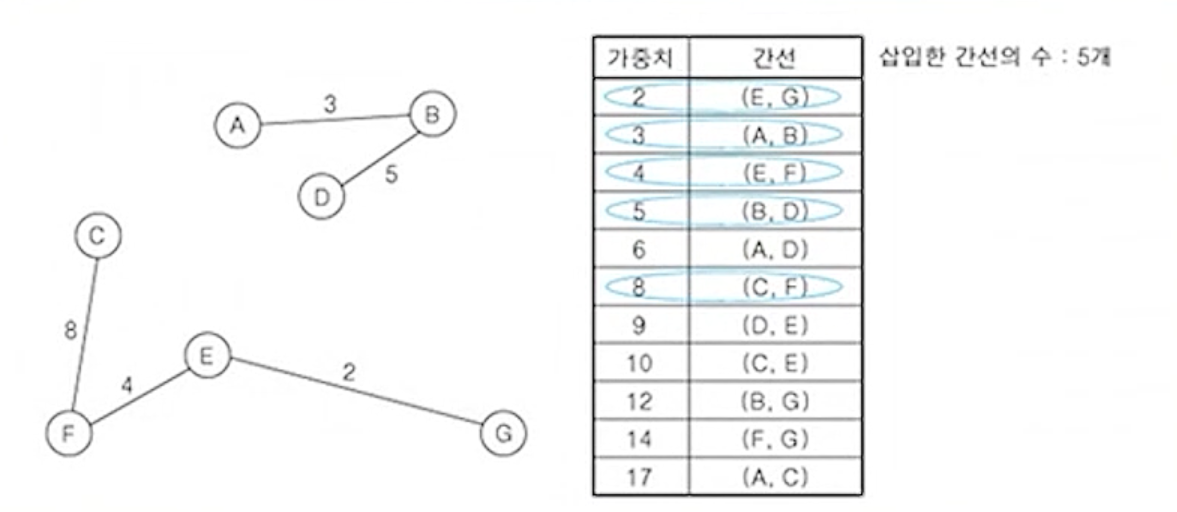
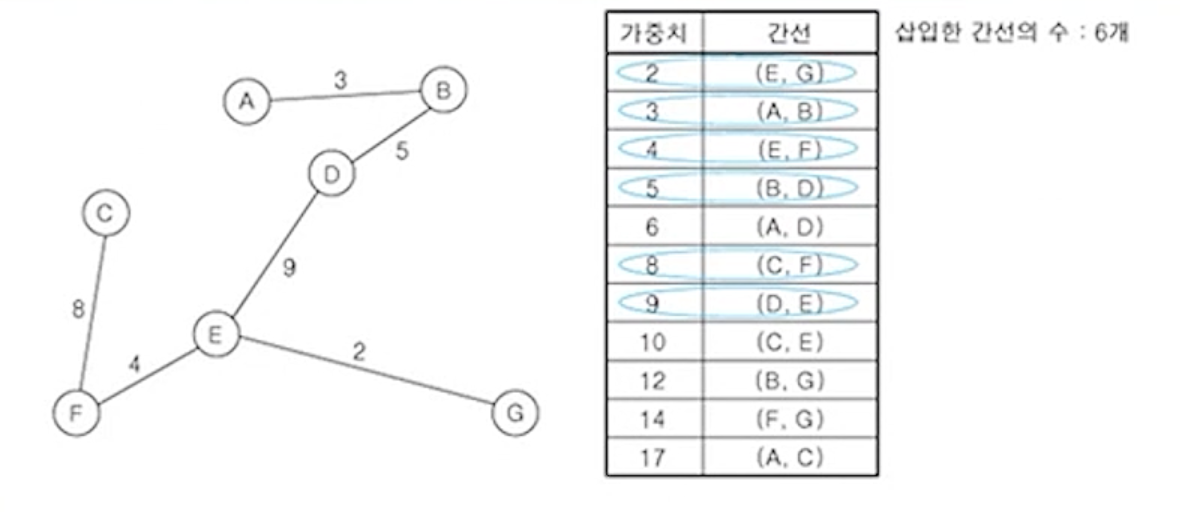
(7) 나머지 간선 중에서 나머지 가중치가 가장 작은 간선 (D,E) 삽입

• 현재 삽입한 간선의 수 : 6개