자료 구조 - Prime 알고리즘

• 간선을 정렬하지 않고 하나의 정점에서 시작하여 트리를 확장해 나가는 방법

1. Prime 알고리즘의 개요

• 그래프 G에서 시작 정점을 선택
• 선택한 정점에 부속된 모든 간선 중에서 가중치가 가장 작은 간선을 연결하여 트리를 확장
• 이전에 선택한 정점과 새로 확장된 정점에 부속된 모든 간선 중에서 가중치가 가장 작은 간선을 삽입
• 이때 사이클을 형성하는 간선은 삽입할수 없으므로 그다으므로 가중치가 작은 간선을 선택
• 그래프 G에서 n-1개의 간선을 삽입할 때 까지 앞 단계를 반복
• 그래프 G의 간선이 n-1개가 되면 최소 비용 신장 트리가 완성됨

1) Prime 알고리즘의 이용

• Prime 알고리즘을 이용하여 G10의 최소 비용 신장 트리 만들기

(1) 초기 상태 : 그래프 G10의 정점 중에서 정점 A를 시작 정점으로 선택

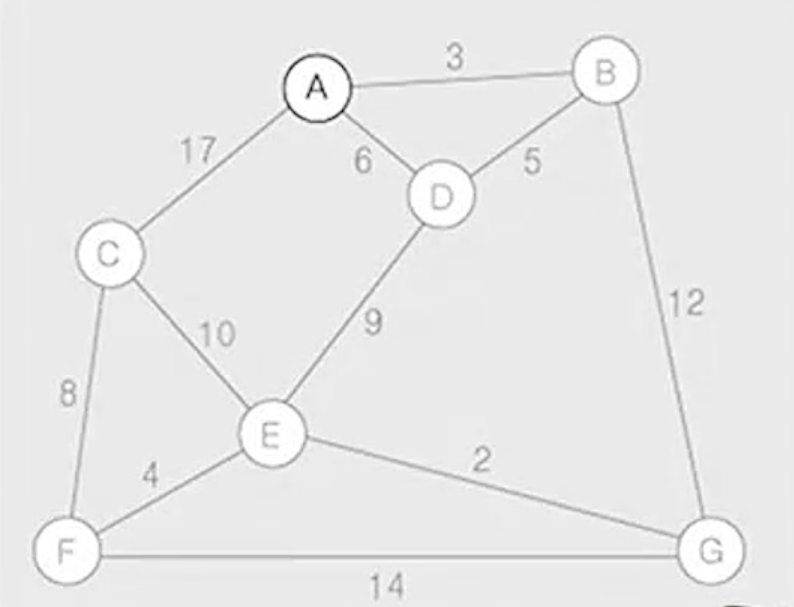
(2) 정점 A에 부속된 간선 중에서 가중치가 가장 작은 간선 (A,B)를 삽입

• 현재 삽입한 간선의 수 : 1개

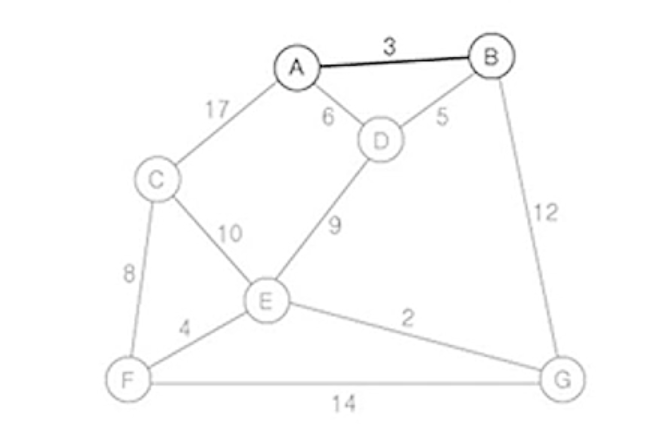
(3) 현재 확장된 트리의 정점 A, B에 부속된 간선 중에서

• 가중치가 가장 작은 간선 (B,D)를 삽입
• 현재 삽입한 간선의 수 : 2개

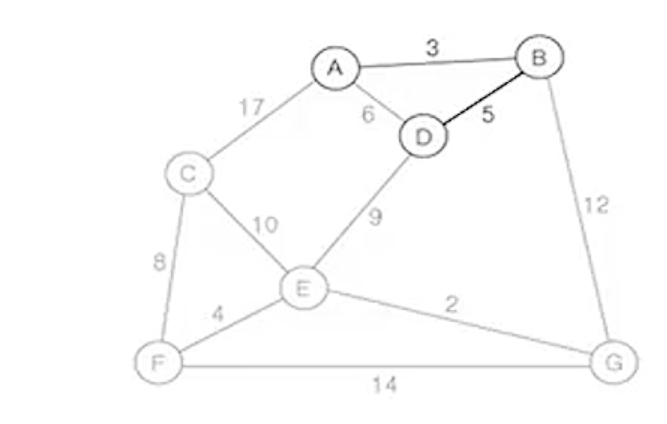
(4) 현재 확장된 트리의 정점 A, B, D에 부속된 간선 중에서

• 가중치가 가장 작은 간선 (A,D)를 삽입
• 현재 확장된 트리의 정점 A,B,D에 부속된 간선중에서 가중치가 가장 작은 간선 (E,G)를 삽입하면 A-B-D-A의
  사이클이 생성되므로 삽입할 수 없음
• 따라서 그 다음으로 가중치가 가장 작은 간선 (D,E)삽입
• 삽입 불가능한 간선 : (A,D)
• 현재 삽입한 간선의 수 : 3개

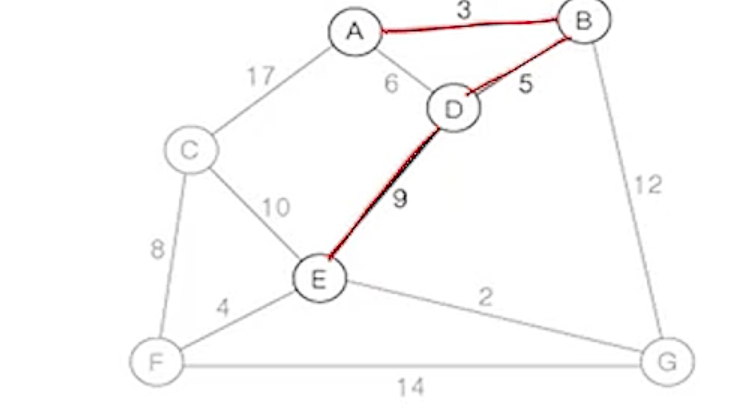
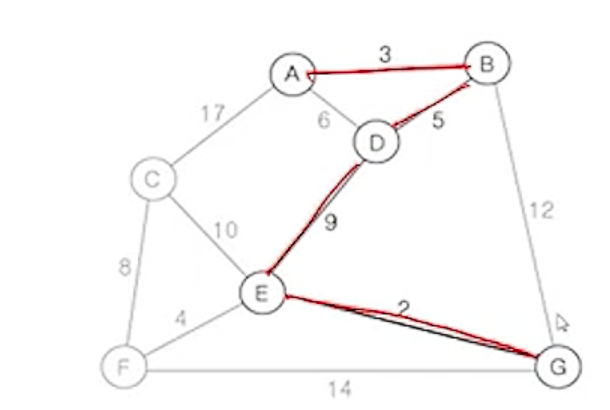
(5) 현재 확장된 트리의 정점 A, B, D, E에 부속된 간선 중에서

• 가중치가 가장 작은 간선 (E,G)를 삽입
• 삽입 불가능한 간선 : (A,D)
• 현재 삽입한 간선의 수 : 4개

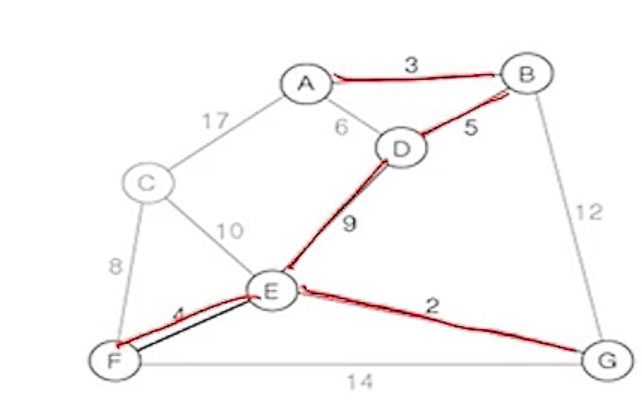
(6) 현재 확장된 트리의 정점 A, B, D, E, G에 부속된 간선 중에서

• 가중치가 가장 작은 간선 (E,F)를 삽입
• 삽입 불가능한 간선 : (A,D)
• 현재 삽입한 간선의 수 : 5개

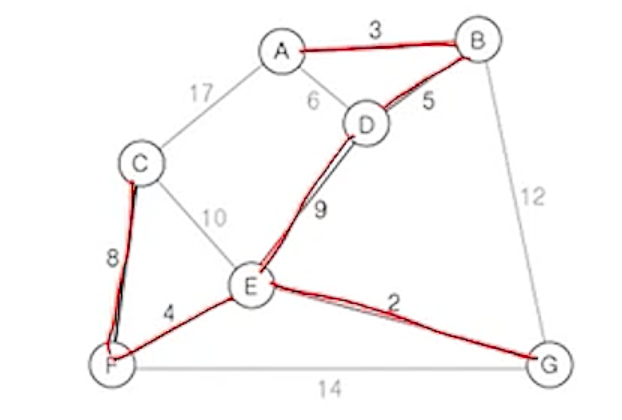
(7) 현재 확장된 트리의 정점 A, B, D, E, F, G에 부속된 간선 중에서

• 가중치가 가장 작은 간선 (C,F)를 삽입
• 삽입 불가능한 간선 : (A,D)
• 현재 삽입한 간선의 수 : 6개
• 현재 남은 간선의 수 6개 이므로 알고리즘 수행을 종료하고 신장 트리 완성

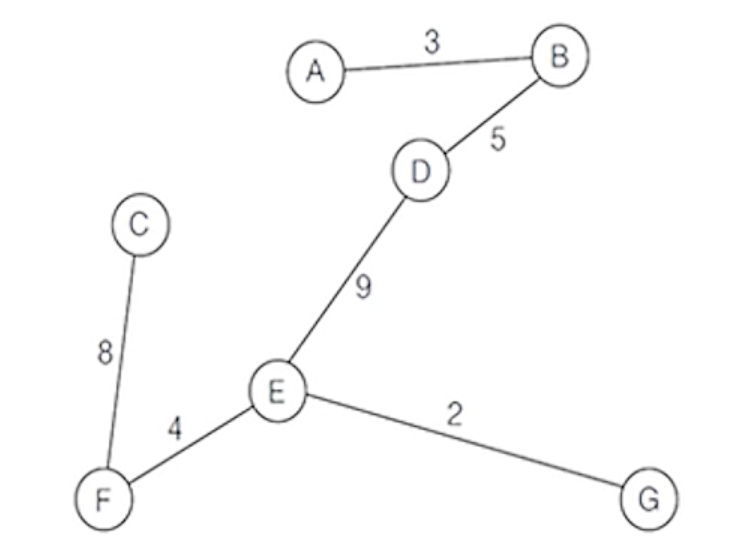
(8) G10의 최소 비용 신장 트리