자료 구조 - 정렬 2 (삽입 정렬)

1. 삽입 정렬

• 정렬되어있는 부분집합에 정렬할 새로운 원소의 위치를 찾아 삽입하는 방법

1) 개요

• 정렬할 자료를 두개의 부분집합 S와 U로 가정
• 부분집합 S : 정렬된 앞부분의 원소들
• 부분집합 U : 아직 정렬되지 않은 나머지 원소들

(1)

• 정렬되지 않은 부분집합 U의 원소를 하나씩 꺼내서 이미 정렬되어있는 부분집합 S의 마지막 원소부터 비교하면서
  위치를 찾아 삽입
• 삽입 정렬을 반복하면서 부분집합 S의 원소는 하나씩 느릴고 부분집합 U의 원소는 하나씩 감소
• 부분집합 U가 공집합이되면 삽입 정렬이 완성

2) 수행 과정

• 정렬되어 있지 않은 {69,10,30,2,16,8,31,22}의 자료들을 삽입 정렬 방법으로 정렬하는 과정

(1) 초기 상태

• 첫 번째 원소는 정렬되어있는 부분 집합 S로 생각하고 나머지 원소들은 정렬되지 않은 원소들의 부분 집합 U로 생각

  S = {69}, U = {10,30,2,16,8,31,22}

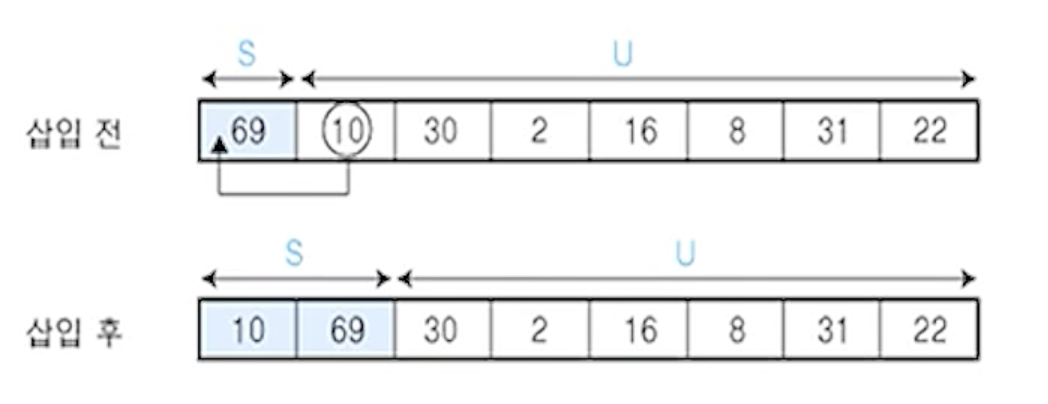
(2)

• U의 첫 번째 원소 10을 S의 마지막 원소 69와 비교하여 (10 < 69)이므로 원소 10은 원소 69의 앞자리가 됨
• 더 이상 비교할 S의 원소가 없으므로 찾은 위치에 원소 10을 삽입함

  S = {10,69}, U = {30,2,16,8,31,22}

(3)

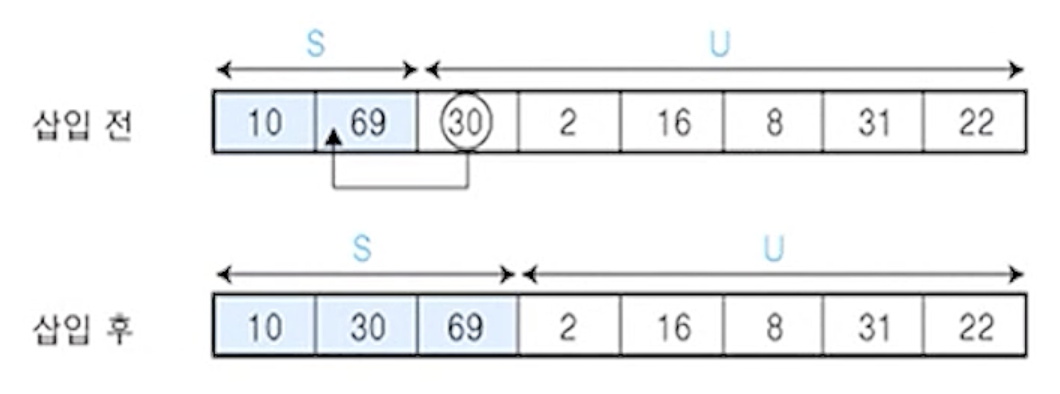
• U의 첫 번째 원소 30을 S의 마지막 원소 69와 비교하여 (30 < 69)이므로 원소 10은 원소 69의 앞자리 원소 10과 비교
• (30>10) 이므로 원소 10과 69사이에 삽입

  S = {10,30,69}, U = {2,16,8,31,22}

(4)

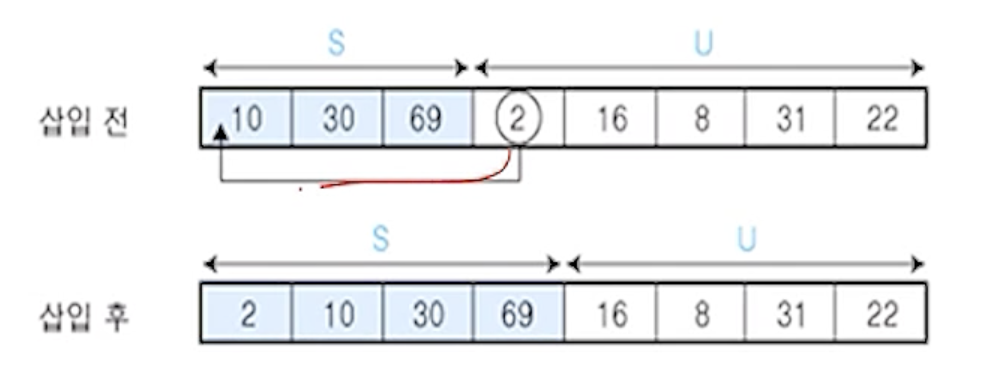
• U의 첫 번째 원소 2를 S의 마지막 원소 69와 비교하여 (2 < 69)이므로 원소 69의 앞자리 원소 30과 비교
• (2 < 30)이므로 다시 그 앞자리 원소 10과 비교
• (2 < 10)이므로 더 이상 비교할 S의 원소가 없으므로 원소 10앞에 삽입함

  S = {2,10,30,69}, U = {16,8,31,22}

(5)

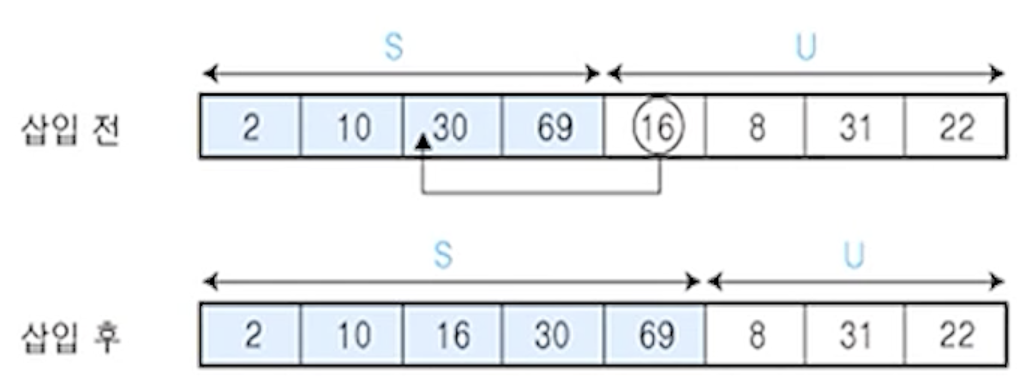
• U의 첫 번째 원소 2를 S의 마지막 원소 69와 비교하여 (16 < 69)이므로 원소 69의 앞자리 원소 30과 비교
• (16 < 30)이므로 그 앞자리 원소 10과 비교
• (16 > 10)이므로 원소 10과 30사이에 삽입

  S = {2,10,16,30,69}, U = {8,31,22}

(6)

• U의 첫 번째 원소 8를 S의 마지막 원소 69와 비교하여 (8 < 69)이므로 원소 69의 앞자리 원소 30과 비교
• (8 < 30)이므로 다시 그 앞자리 원소 16과 비교
• (8 < 16)이므로 다시 그 앞자리 원소 10과 비교
• (8 < 10)이므로 다시 그 앞자리 원소 2과 비교
• (8 > 2)이므로 원소 2와 10사이에 삽입

  S = {2,8,10,16,30,69}, U = {31,22}

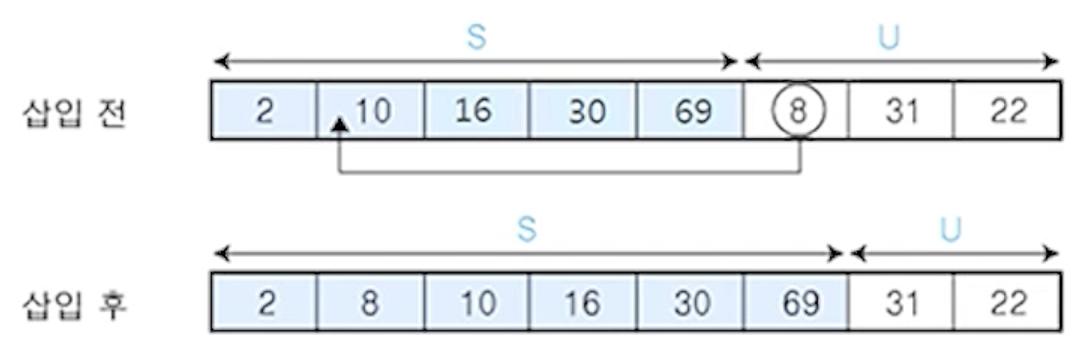
(7)

• U의 첫 번째 원소 31를 S의 마지막 원소 69와 비교하여 (31 < 69)이므로 원소 69의 앞자리 원소 30과 비교
• (31 > 30)이므로 원소 30과 69사이에 삽입

  S = {2,8,10,16,30,31,69}, U = {22}

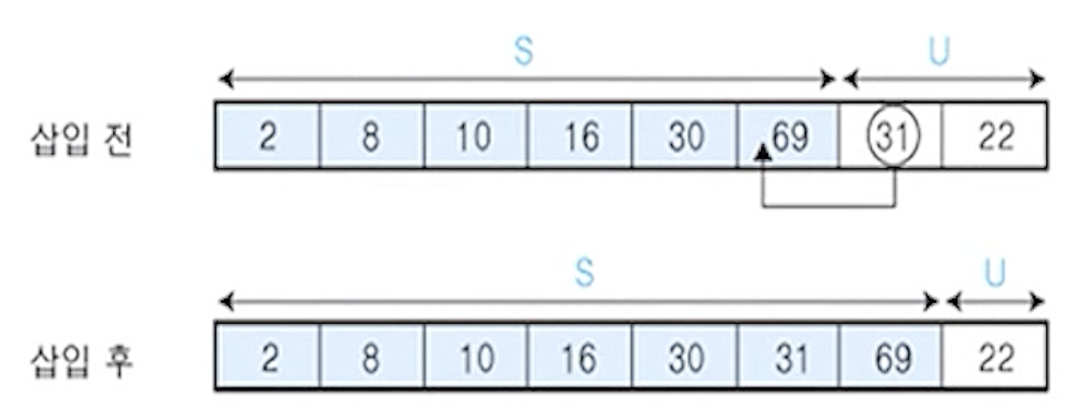
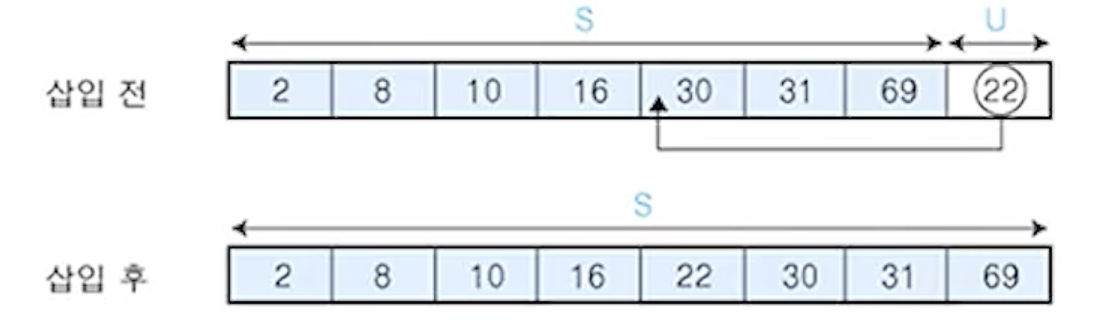
(8)

• U의 첫 번째 원소 22를 S의 마지막 원소 69와 비교하여 (22 < 69)이므로 원소 69의 앞자리 원소 31과 비교
• (22 > 31)이므로 그 앞자리 원소 30과 비교
• (22 < 30)이므로 그 앞자리 원소 16과 비교
• (22 > 16)이므로 원소 16과 30사이에 삽입

  S = {2,8,10,16,22,30,31,69}, U = {}

• U가 공집합이 되었어므로 실행을 종료

3) 삽입 정렬 알고리즘

  insertionSort(a[],n)
      for( i <- 1; i < n; i <- i + 1){

            temp <- a[i];
            j <- i;
            if( a[j-1] > temp) then move <- true;
            else move <- false;
            while (move) do{
              a[j] <- a[j-1];
              j <- j-1;
              if( j > 0 and a[j-1] > temp) then move <- true;
              else move <- false;
            }
            a[j] <- temp;
      }
  end insertionSort()

(1) 메모리 공간

• n개의 원소에 대하여 n개의 메모리 사용

(2) 연산 시간

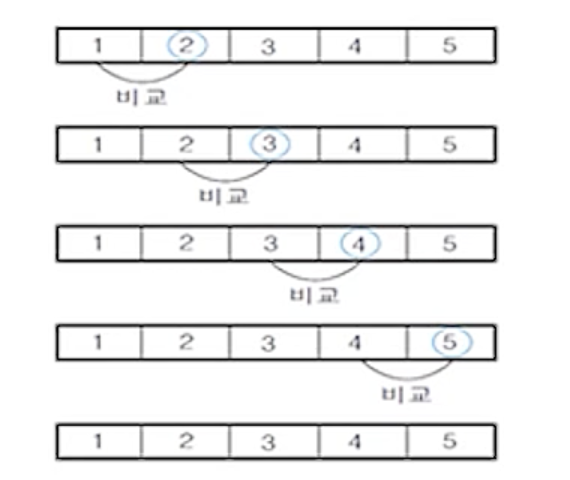
(2-1) 최선의 경우

• 원소들이 이미 정렬되어 있어서 비교횟수가 최소인 경우
• 이미 정렬되어 있는 경우에는 바로 앞자리 원소와 한번만 비교함
• 전체 비교횟수 = n-1
• 시간 복잡도 : O(n)

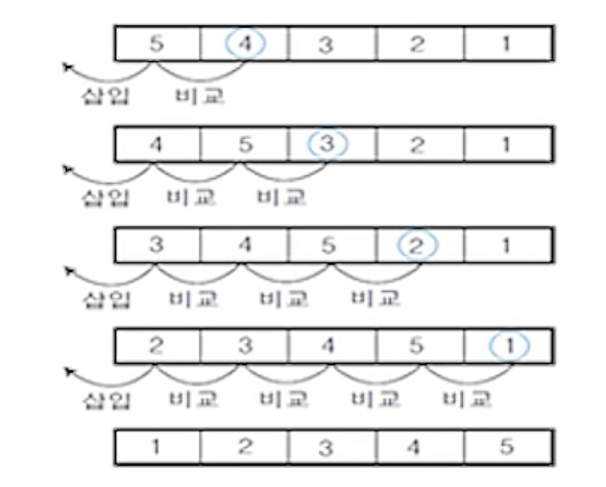
(2-2) 최악의 경우

• 모든 원소가 역순으로 되어있어서 비교횟수가 최대인 경우
• 전체 비교횟수 = 1+2+3+ … + (n-1) = n(n-1)/2
• 시간 복잡도 : O(n(2승))

(2-3)

• 삽입 정렬의 평균 비교횟수 = n(n-1)/4
• 평균 시간 복잡도 : O(n(2승))