자료 구조 - 정렬 2 (기수 정렬)

1. 기수 정렬

• 원소의 키값을 나타내는 기수를 이용한 정렬 방법
• 정렬할 원소의 키 값에 해당하는 버킷에 원소를 분배하였다가 버킷의 순서대로 원소를 꺼내는 방법을 반복하면서 정렬
• 원소의 키를 표현하는 기수만큼의 버킷 사용
• 매 단계마다 원소들을 버킷 순서대로 꺼내 다음 단계의 기수 정렬을 수행하므로 큐를 사용하여 버킷을 만듦

1) 개요

(1) 10진수로 표현된 키 값을 가진 원소의 정렬 방법

(1-1) 키 값의 자리수 만큼 기수 정렬을 반복

• 키 값의 일의 자리에 대해서 기수 정렬을 수행
• 다음 단계에서는 키 값의 십의 자리에 대해서
• 그리고 그 다음 단계에서는 백의 자리에 대해서 기수 정렬 수행

2) 수행 과정

• 정렬되어 있지 않은 {69,10,30,2,16,8,31,22}의 자료들을 셸 정렬 방법으로 정렬하는 과정
• 키 값이 두자리 십진수 이므로, 10개의 버킷을 사용하여 기수 정렬을 두번 반복함

(1) 초기상태

• 큐를 사용하여 0부터 9까지 10개의 버킷을 만듦

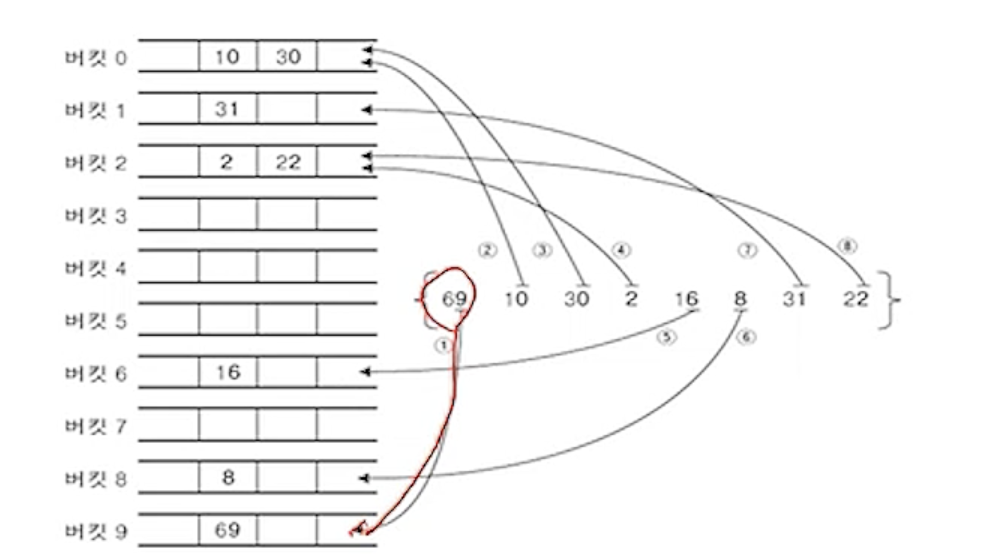
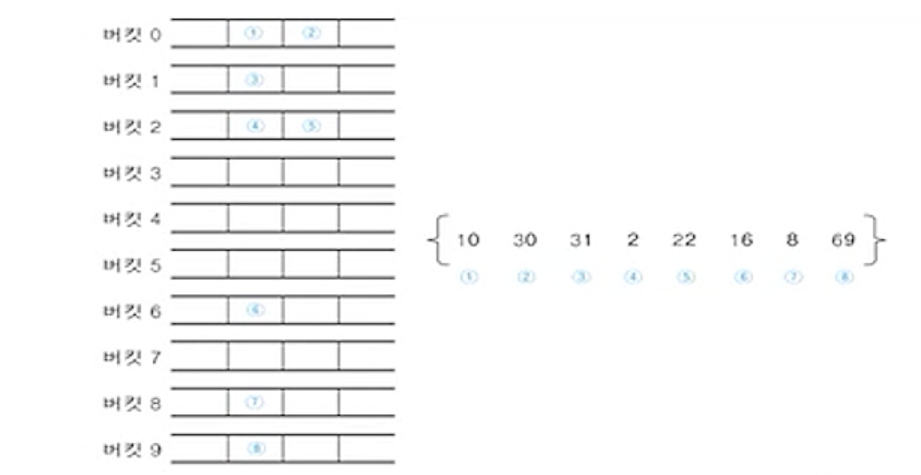
(2) 키 값의 일의 자리에 대해서 기수 정렬 수행

• 버킷에 분배된 원소들을 순서대로 꺼내서 저장

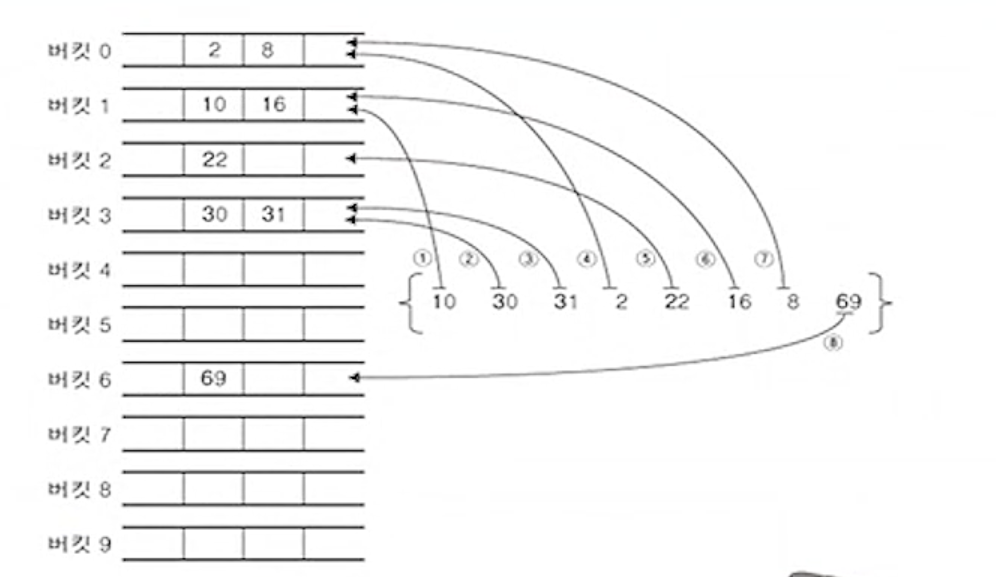
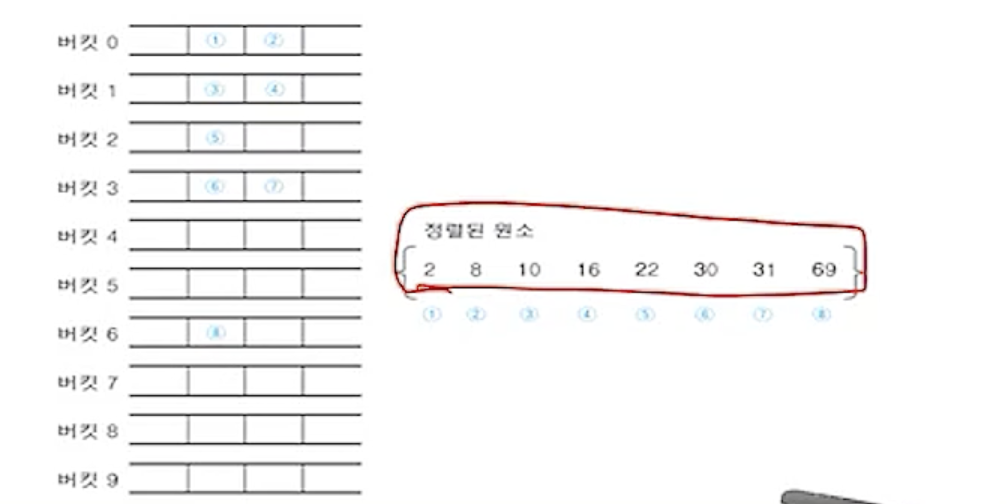
(3) 키 값의 십의 자리에 대하여 기수 정렬 수행

• 버킷에 분배된 원소들을 순서대로 꺼내서 저장

3) 기수 정렬 알고리즘

  radixSort(a[],n)
      for(k <- 1; k <= n; k <- k +1 ) do{

          for( i <-0; i < n; i <- i + 1 ) do {

              // k번째 자리수 값에 따라서 해당 버킷에 저장
              enQueue(Q[k], a[i]);
          }
          p <- -1;
          for (i <- 0; i<= 9; i <= i + 1)do {
              while( Q[i] != null)do{
                p <- p + 1;
                a[p] <- deQueue(Q[i]);
              }
          }
      }
  end radixSort()

(1) 메모리 사용 공간

• 원소 n개에 대해서 n개의 메모리 공간 사용
• 기수 r에 따라 버킷 공간이 추가로 필요

(2) 연산 시간

• 연산 시간을 정렬할 원소의 수 n과 키 값의 자리수 d와 버킷의 수로 결정하는 기수 r 따라서 달라짐
• 정렬할 원소 n개를 r개의 버킷에 분배하는 작업 : (n+r)
• 이 작업을 자릿수 d만큼 반복
• 수행할 전체 작업 : d(n+r)
• 시간 복잡도 : O(d(n+r))