자료 구조 - 정렬 3 (병합 정렬)

1. 병합 정렬

• 여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방법
• 부분집합으로 분할하고, 각 부분집합에 대해서 정렬 작업을 완성 함
• 정렬된 부분집합들을 다시 결합하는 분할 정복 기법 사용

1) 개요

(1) 병합 정렬 방법의 종류

(1-1) 2-way 병합

• 2개의 정렬된 자료의 집합을 결합하여 하나의 집합으로 만드는 병합 방법

(1-2) n-way 병합

• n개의 정렬된 자료의 집합을 결합하여 하나의 집합으로 만드는 병합 방법

(2) 2-way 병합 정렬

• 세 가지 기본 작업을 반복 수행하면서 완성

(2-1) 분할 (divide)

• 입력 자료를 같은 크기의 부분집합 2개로 분할함

(2-2) 정복 (conquer)

• 부분집합의 원소들을 정렬함
• 부분집합의 크기가 충분히 작지 않으면 순환호출을 이용하여 다시 분할 정복 기법을 사용

(2-3) 결합 (combine)

• 정렬된 부분집합을 하나의 집합으로 결합

2) 수행 과정

• 정렬되어 있지 않은 {69,10,30,2,16,8,31,22}의 자료들을 셸 정렬 방법으로 정렬하는 과정

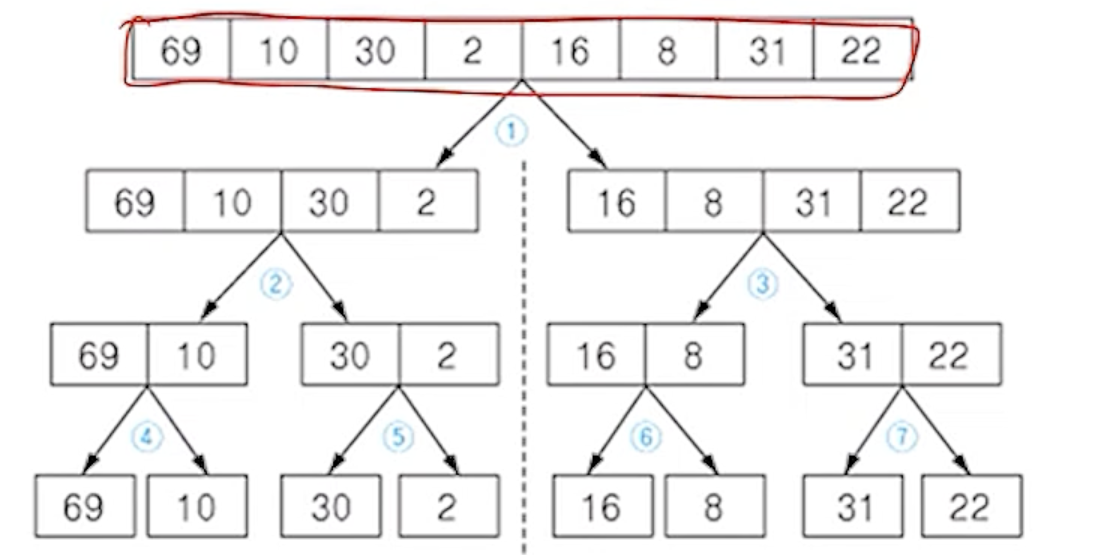
(1) 분할 단계

• 정렬할 전체 자료의 집합에 대해서 최소 원소의 부분집합이 될 때까지 분할작업을 반복하여 1개의 원소를 가진 부분집합
  8개를 만듦

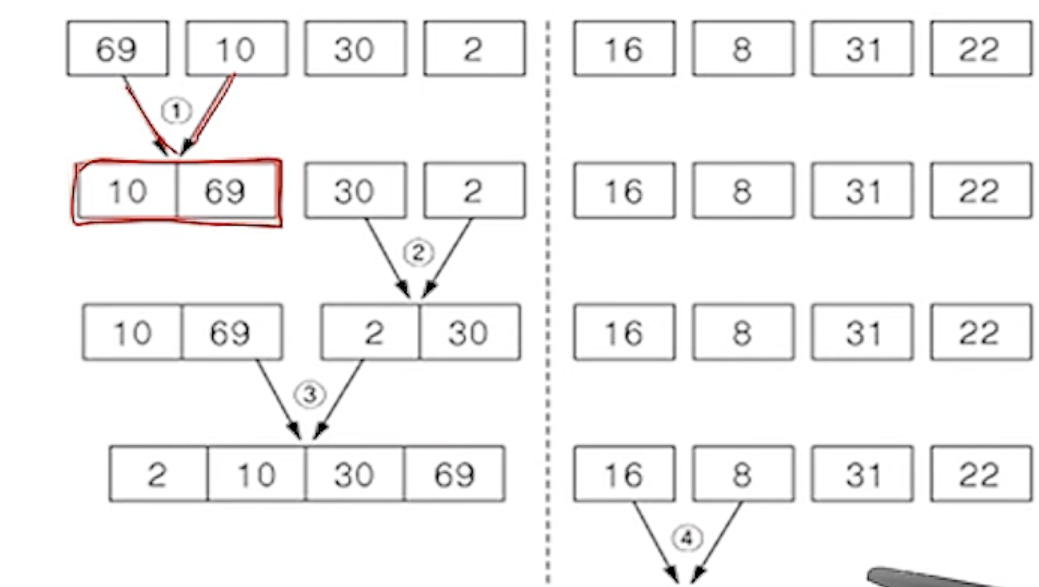
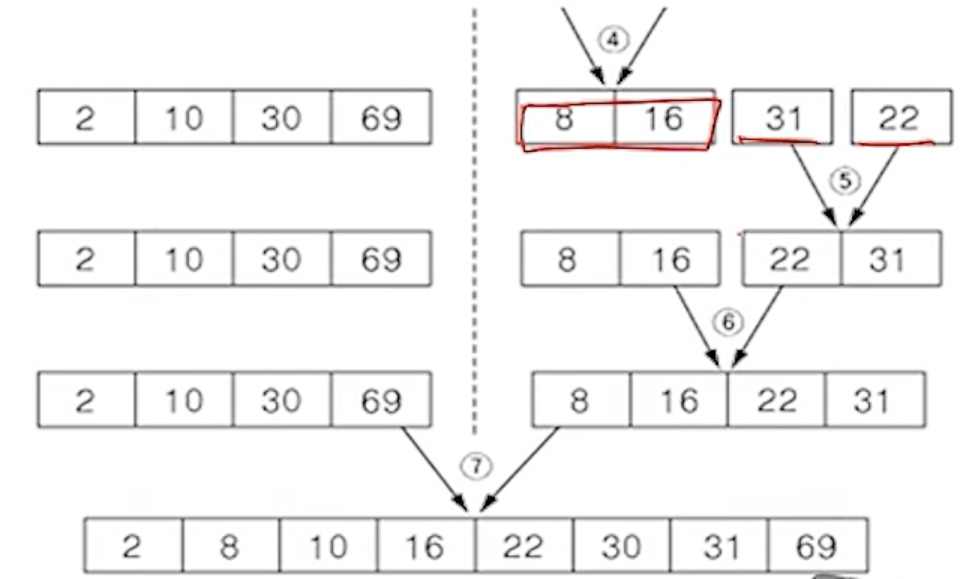
(2) 병합 단계

• 2개의 부분집합을 정렬하면서 하나의 집합으로 병합함
• 8개의 부분집합이 1개로 병합될 때까지 반복

3) 병합 정렬 알고리즘

  mergeSort(a[],m,n)
        if(a[m:n]의 원소수 > 1) then {

            // 전체 집합을 두 개의 부분집합으로 분할;
            mergeSort(a[], m, middle);
            mergeSort(a[], middle+1, n);
            merge(a[m:middle], a[middle+1:n]);
        }
  end mergeSort()

(1) 메모리 사용 공간

• 각 단계에서 새로 병합하여 만든 부분집합을 저장할 공간이 추가로 필요
• 원소 n개에 대하여 (2 X n)개의 메모리 공간 사용

(2) 연산 시간

(2-1) 분할 단계

• n개의 원소를 분할하기 위해서 log2n번의 단계 수행

(2-2) 병합 단계

• 부분집합의 원소를 비교하면서 병합하는 단계에서 최대 n번의 비교연산 수행

(2-3) 전체 병합 정렬의 시간 복잡도

• O(n log2n)