자료 구조 - 정렬 3 (히프 정렬)

1. 히프 정렬

• 8장의 히프 자료구조를 이용한 정렬 방법
• 히프에서는 항장 가장 큰 원소가 루트 노드가 되고 삭제 연산을 수행하면 항상 루트 노드의 원소를 삭제하여 반환

1) 개요

(1) 최대 히프

• 최대 히프에 대해서 원소의 개수만큼 삭제 연산을 수행하여 내림차순으로 정렬 수행

(2) 최소 히프

• 최소 히프에 대해서 원소의 개수만큼 삭제 연산을 수행하여 오름차순으로 정렬 수행

(3) 수행 방법

1. 정렬할 원소들을 입력하여 최대 히프 구성
2. 히프에 대해서 삭제 연산을 수행하여 얻은 원소를 마지막 자리에 배치
3. 나머지 원소에 대해서 최대 히프로 재구성 원소의 개수만큼 2~3을 반복 수행

2) 수행 과정

• 정렬되어 있지 않은 {69,10,30,2,16,8,31,22}의 자료들을 셸 정렬 방법으로 정렬하는 과정

(1) 초기 상태

• 정렬할 원소가 8개 이므로 노드가 8개인 완전 이진 트리를 만들고, 최대 히프로 구성

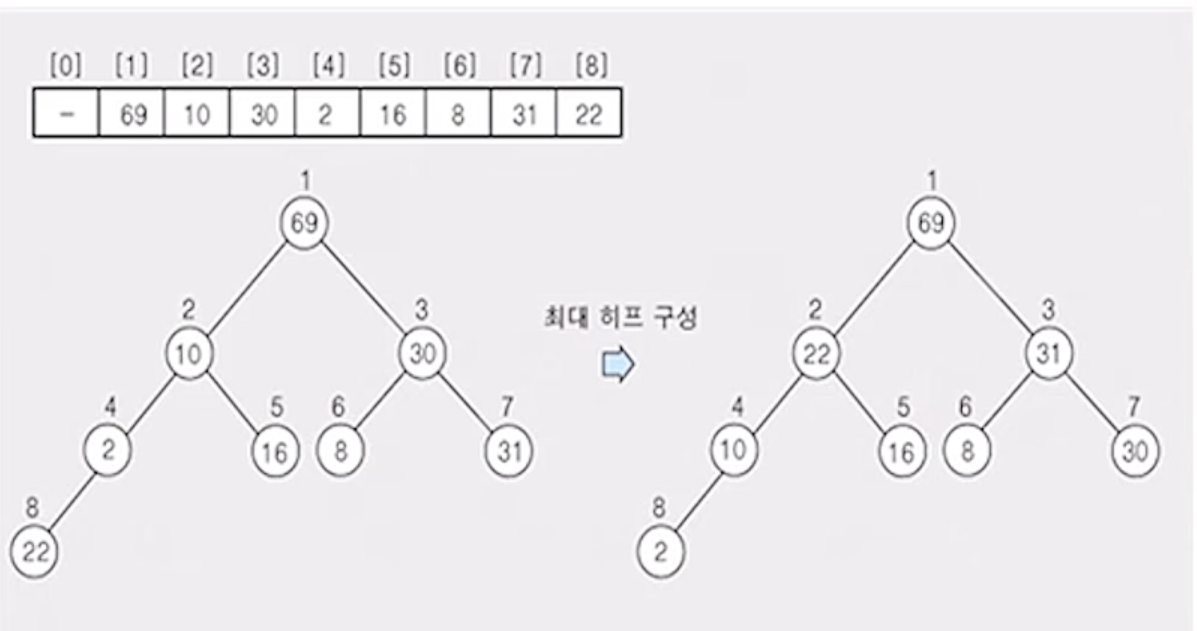
(2) 히프에 삭제 연산을 수행 - 원소 69

• 노드의 원소 69를 구해서 배열의 마지막 자리에 저장
• 나머지 원소들에 대해서 최대 히프로 재구성

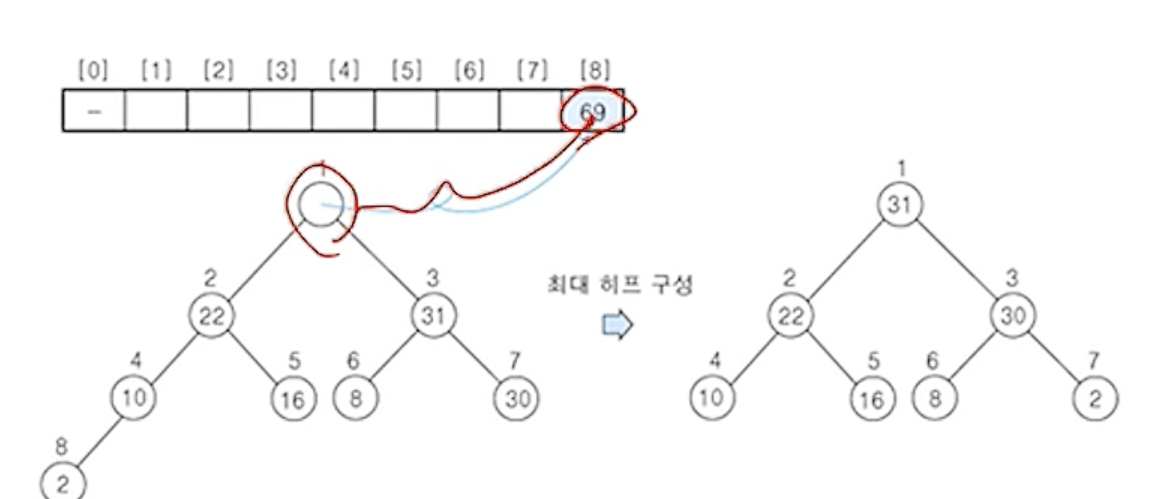
(3) 히프에 삭제 연산을 수행 - 원소 31

• 노드의 원소 31를 구해서 배열의 마지막 자리에 저장
• 나머지 원소들에 대해서 최대 히프로 재구성

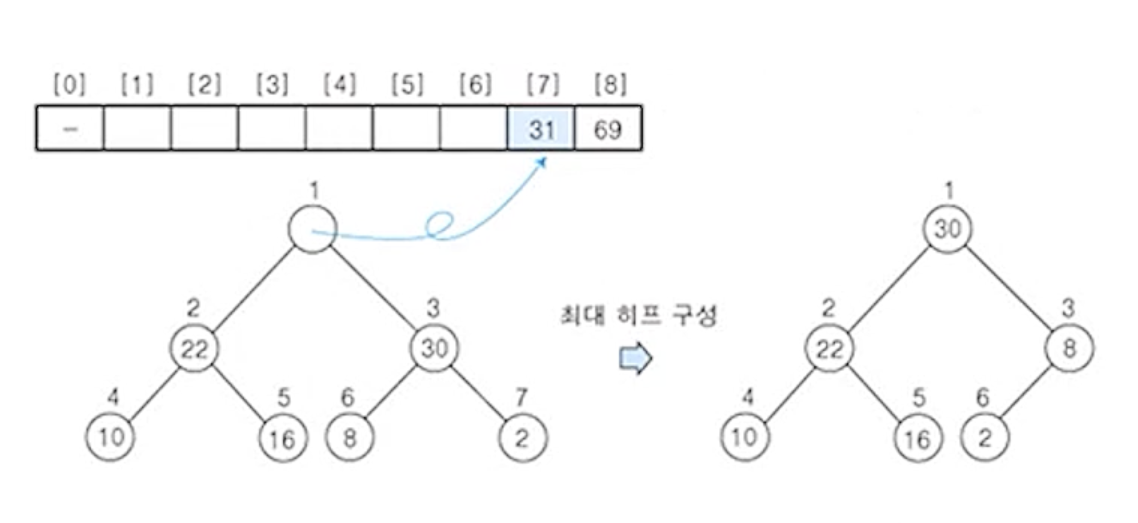
(4) 히프에 삭제 연산을 수행 - 원소 30

• 노드의 원소 30를 구해서 배열의 마지막 자리에 저장
• 나머지 원소들에 대해서 최대 히프로 재구성

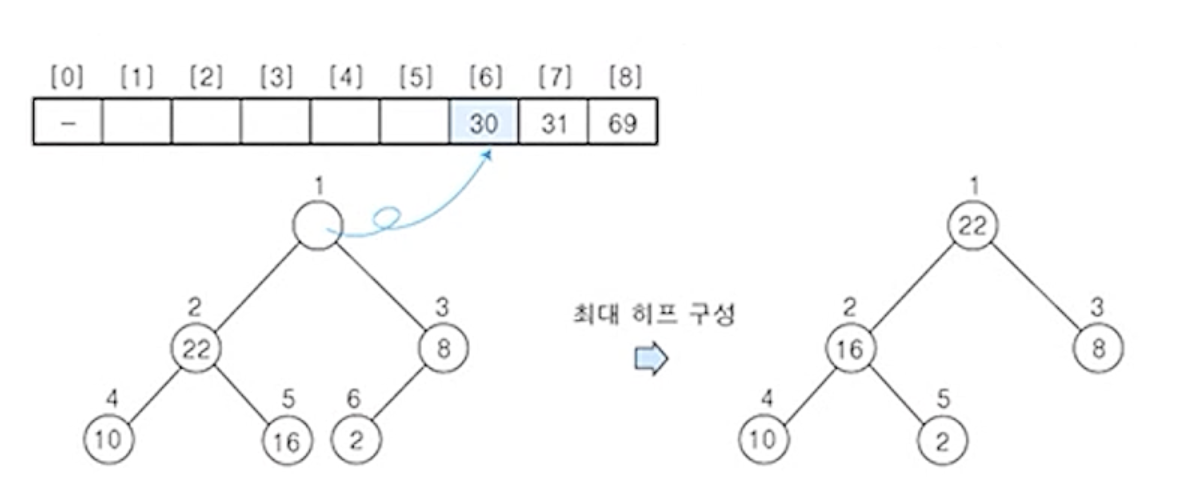
(5) 히프에 삭제 연산을 수행 - 원소 22

• 노드의 원소 22를 구해서 배열의 마지막 자리에 저장
• 나머지 원소들에 대해서 최대 히프로 재구성

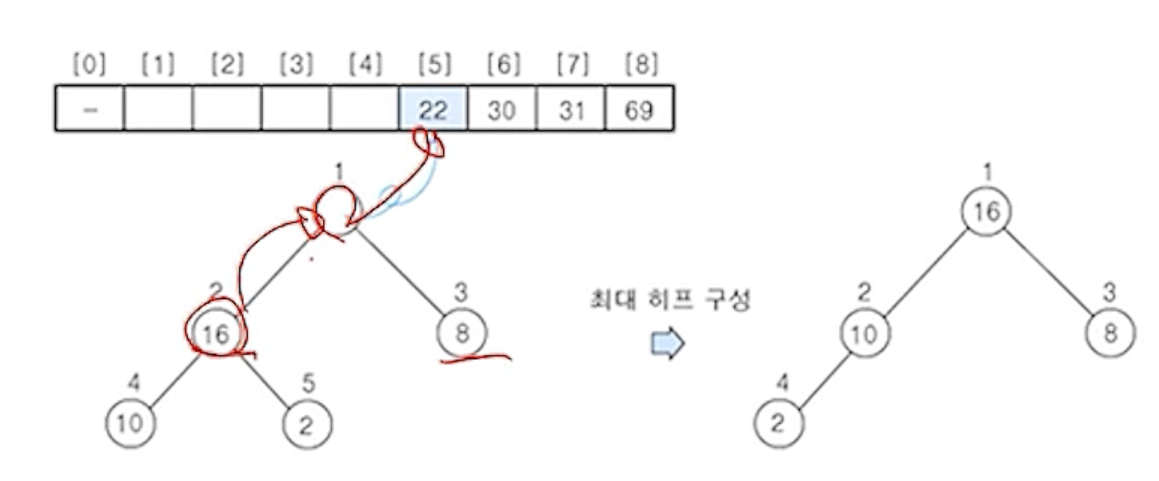
(6) 히프에 삭제 연산을 수행 - 원소 16

• 노드의 원소 16를 구해서 배열의 마지막 자리에 저장
• 나머지 원소들에 대해서 최대 히프로 재구성

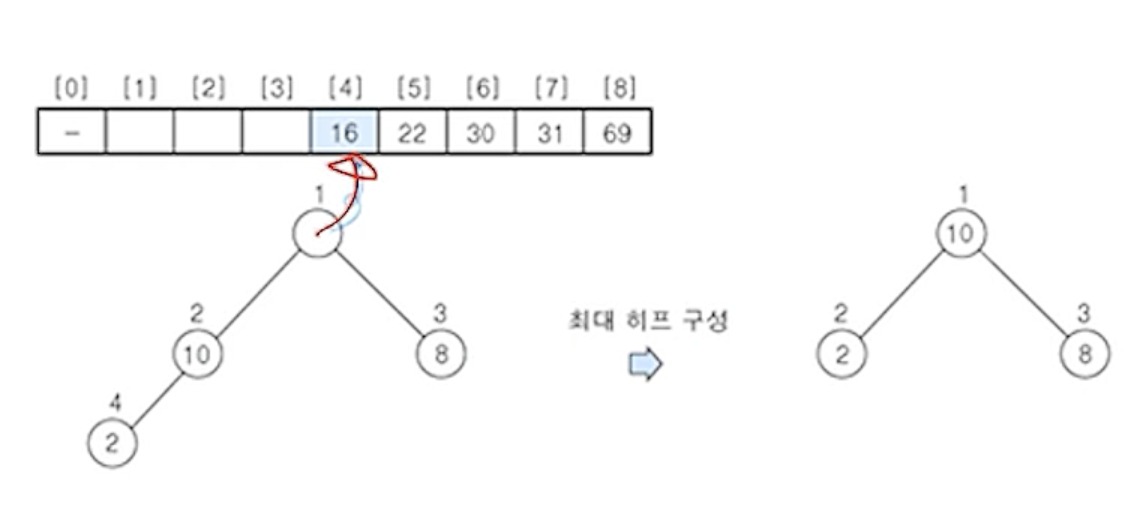
(4) 히프에 삭제 연산을 수행 - 원소 10

• 노드의 원소 10를 구해서 배열의 마지막 자리에 저장
• 나머지 원소들에 대해서 최대 히프로 재구성

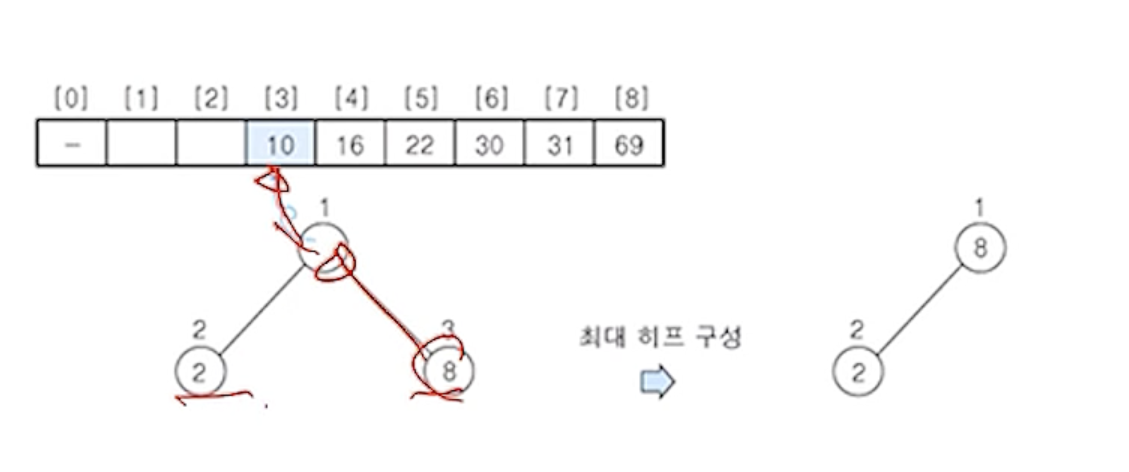
(4) 히프에 삭제 연산을 수행 - 원소 8

• 노드의 원소 8를 구해서 배열의 마지막 자리에 저장
• 나머지 원소들에 대해서 최대 히프로 재구성

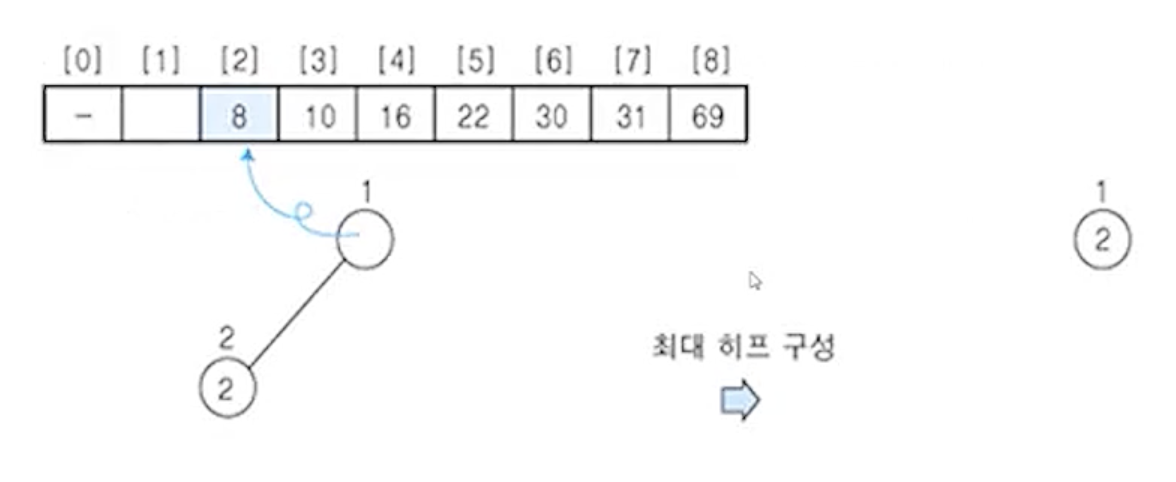
(4) 히프에 삭제 연산을 수행 - 원소 2

• 노드의 원소 2를 구해서 배열의 마지막 자리에 저장
• 나머지 원소들에 대해서 최대 히프로 재구성하는데 공백 히프가 되었으므로 히프 정렬 종료

3) 히프 정렬 알고리즘

  heapSort(a[])
      n <- a.length - 1;
      for (i <- n/2; i >= 1; i <- i - 1) do { // 배열 a[]를 히프로 변환
          makeHeap(a, i, n);
      }
      for (i <- n-1; i >= 1; i <- i - 1) do {
          temp <- a[1];       // 히프의 루트 노드 원소를
          a[1] <- a[i+1];     // 배열의 비어있는
          a[i+1] <- temp;     // 마지막 자리에 저장

          makeHeap(a, 1, i);
      }
  end heapSort()

• 히프 재구성 알고리즘

  makeHeap(a[], h, m)
      for(j <- 2*h; j <=m; j <- 2*j) do {

          if( j < m ) then
              if( a[j] < a[j+1]) then j <- j + 1;
          if( a[h] >= a[j] ) then exit;
          else a[j/2] <- a[j];
      }
      a[j/2] <- a[h];
  end makeHeap()

(1) 메모리 사용 공간

• 원소 n개에 대해서 n개의 메모리 공간 사용
• 크기 n의 히프 공간 저장

(2) 연산시간

(2-1) 히프 재구성 연산 시간

• n개의 노드에 대해서 이진 트리는 log2(n+1)의 레벨을 가지므로 완전 이진트리를 히프로 구성하는 평균시간은
  O(n log2n)
• n개의 노드에 대해서 n번의 히프 재구성 작업 수행
• 평균 시간 복잡도 : O(n log2n)