자료 구조 - 해싱
1. 해싱의 이해
- 산술적인 연산을 이용하여 키가 있는 위치를 계산하여 바로 찾아가는 계산 검색 방식
1) 검색 방법
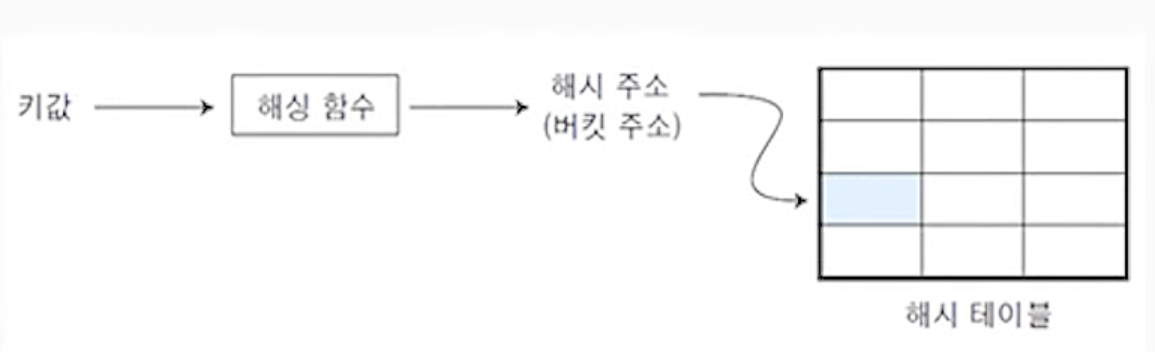
- 키 값에 대해서 해싱 함수를 계산하여 주소를 구하고, 구한 주소에 해당하는 해시 테이블로 바로 이동
- 해당 주소에 찾는 항목이 있으면 검색 성공, 없으면 검색 실패
(1) 해싱 함수
- hashing function
- 키 값을 원소의 위치로 변환하는 함수
(2) 해시 테이블
- hash table
- 해싱 함수에 의해서 계산된 주소의 위치에 항목을 저장한 표
2) 해싱 용어
(1) 충돌 (collision)
- 서로 다른 키 값에 대해서 해싱 함수에 의해 주어진 버킷 주소가 같은 경우
- 충돌이 발생한 경우에 비어있는 슬롯에 동거자 관계로 키 값 저장
(2) 동거자 (synonym)
- 서로 다른 키 값을 가지지만 해싱 함수에 의해서 같은 버킷에 저장된 키 값들
(3) 오버플로우
- 버킷에 비어있는 슬롯이 없는 포화 버킷 상태에서 충돌이 발생하여 해당 버킷에 키 값을 저장할 수 없는 상태
(4) 버킷
(5) 키 값 밀도
- 사용 가능한 전체 키 값들 중에서 현재 헤시 테이블에 저장되어서 실제 사용되고 있는 키 값의 개수 정도

(6) 적재 밀도
- 해시 테이블에 저장 가능한 키 값의 개수 중에서 현재 해시 테이블에 저장되어서 실제 사용되고 있는 키 값의 개수 정도

2. 해싱 함수
1) 해싱 함수의 조건
(1) 해싱 함수는 계산이 쉬어야 함
- 비교 검색 방법을 사용하여 키 값의 비교연산을 수행하는 시간보다 해싱 함수를 사용하여 계산하는 시간이 빨라야
해싱 검색을 사용하는 의미가 있음
(2) 해싱 함수는 충돌이 적어야 함
- 충돌이 많이 발생한다는 것은 같은 버킷을 할당 받는 키 값이 많다는 것
- 비어있는 버킷이 많은데도 어떤 버킷은 오버플로우가 발생할 수 있는 상태가 되므로 좋은 해싱 함수가 될 수 없음
(3) 해시 테이블에 고르게 분포할 수 있도록 주소를 만들어야 함
2) 해싱 함수의 종류
(1) 중간 제곱 함수
- 키 값을 제곱한 결과 값에서 중간에 있는 적당한 비트를 주소로 사용하는 방법
- 제곱한 값의 중간 비트들은 대개 키의 모든 값과 관련이 있기 때문에 서로 다른 키 값은 서로 다른 중간 제곱 함수
값을 갖게 됨

- 킷 값에 대한 2진수를 제곱한 결과값에서 가운데 있는 8비트는
11101001이 된다.
11101001의 10진수 값 233이 해시 테이블의 버킷 주소가 됨- 제곱 결과값에서 주소로 사용하는 비트 수는 해시 테이블의 버킷의 개수에 따라 결정됨
- 버킷이
256개가 있다면 버킷의 주소는 0 ~ 255까지 256개의 값을 사용.
- 256(2(8승))의 값을 만들기 위해 필요한 최소의 비트수는 8비트가 되므로 제곱 결과값에서 8비트를 주소로 사용
(2) 제산 함수
- 함수는 나머지 연산자 mod를 사용하는 방법
- 키 값
k를 해시 테이블의 크기 M으로 나눈 나머지를 해시 주소로 사용
- 제산함수 : h(k) = k mod M
M으로 나눈 나머지 값은 0 ~ (M - 1)이 되므로 해시 테이블의 인덱스로 사용- 해시 주소는 충돌이 발생하지 않고 고르게 분포하도록 생성되어야 하므로 키 값을 나누는 해시 테이블의 크기
M은
적당한 크기의 소수 사용
(3) 승산 함수
- 곱하기 연산을 사용하는 방법
- 키 값
k와 정해진 실수 a를 곱한 결과에서 소수점 이하 부분만을 테이블의 크기 M과 곱하여 그 정수 값을 주소로 사용
(4) 접지 함수
- 키의 비트 수가 해시 테이블 인덱스의 비트 수보다 큰 경우에 주로 사용
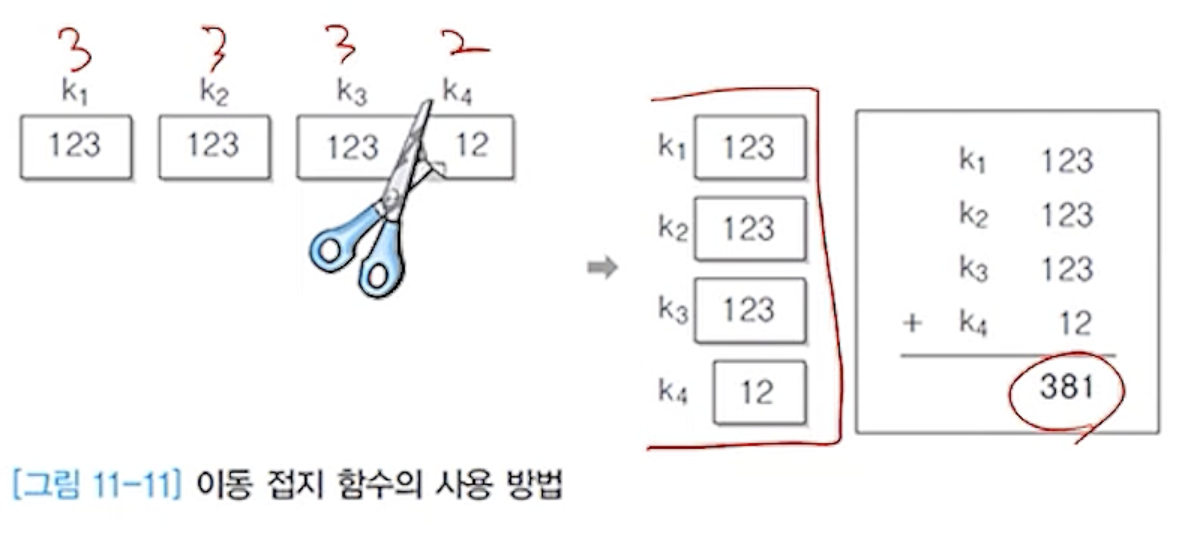
(4-1) 이동 접지 함수
- 각 분할 부분을 이동시켜서 오른쪽 끝자리가 일치하도록 맞추고 더하는 방법
- 예) 해시 테이블 인덱스가 3자리이고 키 값
k가 12312312312인 경우
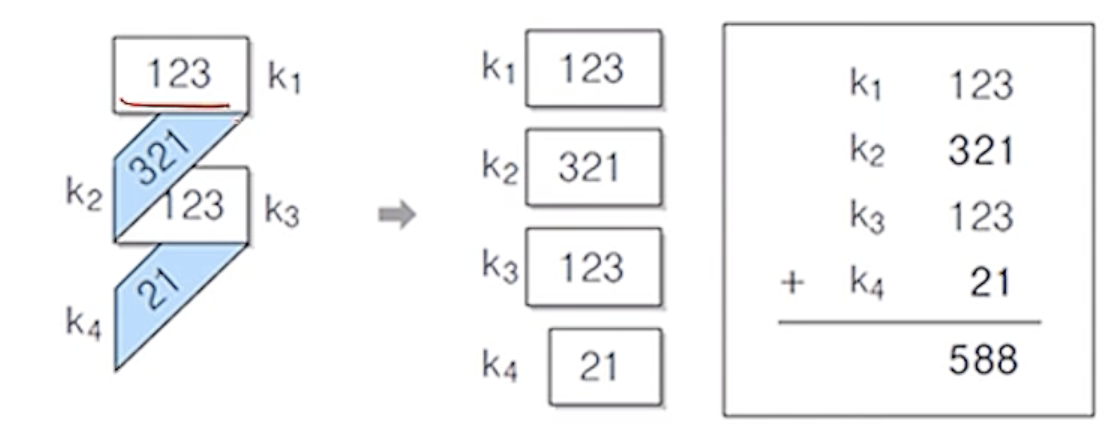
(5) 경계 접지 함수
- 분할된 각 경계를 기준으로 접으면서 서로 마주보도록 배치하고 더하는 방법
- 해시 테이블 인덱스가 3자리이고 키 값
k가 12312312312인 경우
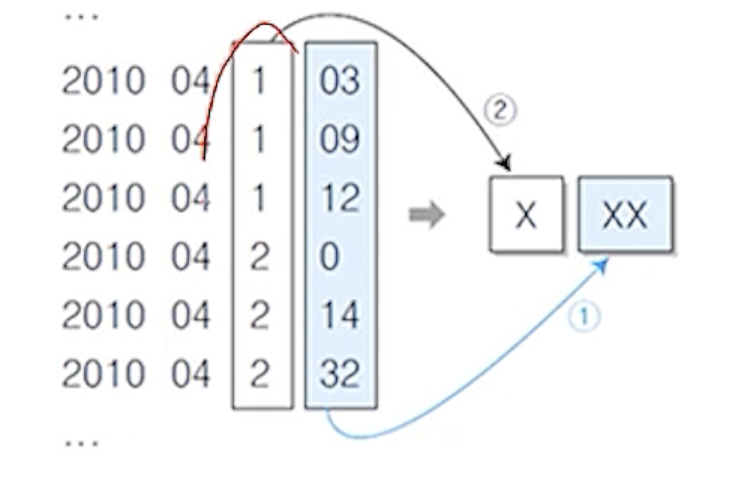
(6) 숫자 분석 함수
- 키 값을 이루고 있는 각 자리수의 분포를 분석하여 해시 주소로 사용하는 방법
- 각 키 값을 적절히 선택한 진수로 변환한 후에
- 각 자리수의 분포를 분석하여 가장 편중된 분산을 가진 자릿수는 생략
- 가장 고르게 분포된 자릿수부터 해시 테이블 주소의 자릿수만큼 차례로 뽑아서 만든수를 역순으로 바꾸어서 주소로 사용
- 에) 키 값이 학번이고 해시 테이블 주소의 자릿수가 3자리인 경우
(7) 진법 변환 함수
- 키 값이 10진수가 아닌 다른 진수일 때
- 10진수로 변혼하고 해시 테이블 주소로 필요한 자릿수만큼만 하위자리의 수를 이용하는 방법
(8) 비트 추출 함수
- 해시 테이블의 크기가
2k일 때 키값을 이진 비트로 놓고 임의의 위치에 있는 비트들을 추출하여 주소로 사용
- 이 방법에서는 충돌이 발생할 가능성이 많으므로 테이블의 일부에 주소가 편중되지 않도록 키 값들의 비트들을 미리 분석








댓글남기기