디지털 공학 개론 - 부울대수의 기본 개념

1. 부울대수란?

1) 부울 대수(Boolean Algebra)

• George Boole이 논리적 프로세스들을 표현하기 위하여 개발한 대수학
• 디지털 논리회로의 분석과 설계의 기본이 되는 수학

2) 부울 대수에 근거하여 표현되는 부울 함수의 구성 요소들

(1) 부울 함수의 예

  F = A + B'C
      A,B,C : 입력 변수들
      F : 출력 변수

(2) 논리 회로 구현

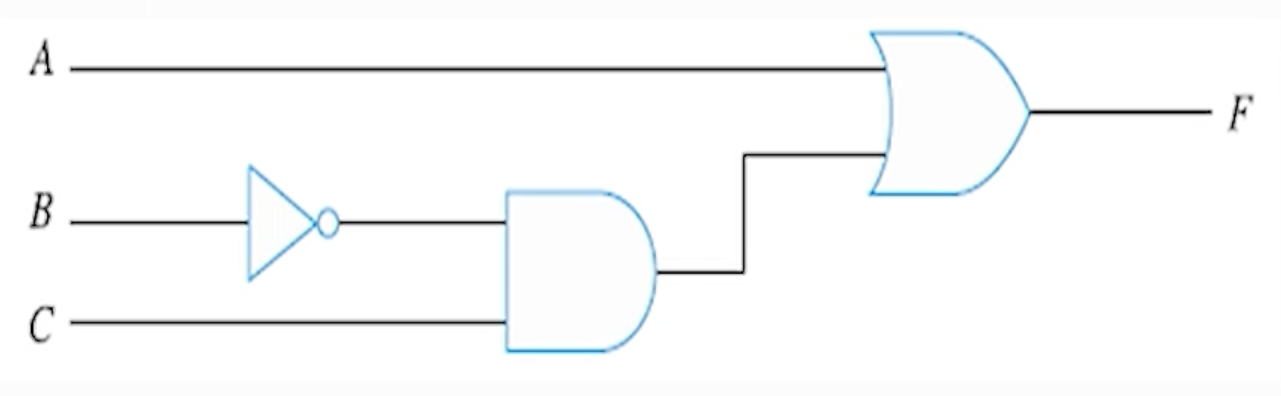
2. 부울연산의 표현

1) 부울 보수(Boolean complement)

  A' 혹은 A (A = 1 -> A' = 0, A = 0 -> A' = 1)

• A프라임으로 읽기로 함
• 인버터로 구현 (F=A’)

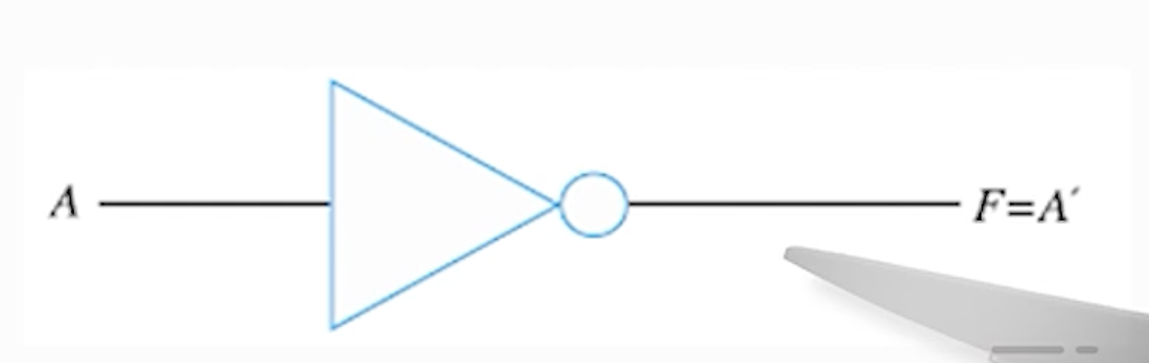
2) 부울 덧셈(Boolean addition)

• OR 게이트로 구현

부울 덧셈의 규칙

  0 + 0 = 0
  0 + 1 = 1
  1 + 0 = 1
  1 + 1 = 1

(1) 입력 변수의 수에 따른 함수의 표현

• 2-변수 OR 함수 : F2 = A + B
• 3-변수 OR 함수 : F3 = A + B + C
• 4-변수 OR 함수 : F4 = A + B + C + D

3) 부울 곱셈(Boolean multiplication)

• AND 게이트로 구현

부울 곱셈의 규칙

  0 * 0 = 0
  0 * 1 = 0
  1 * 0 = 0
  1 * 1 = 1

(1) 입력 변수의 수에 따른 함수의 표현

• 2-변수 AND 함수 : F2 = AB
• 3-변수 AND 함수 : F3 = ABC
• 4-변수 AND 함수 : F4 = ABCD

4) 기타 부울 함수들

(1) NOR 함수 : F = (A+B)’

• (A+B = OR)
• 그뒤에 NOT을 붙임 (인버터)

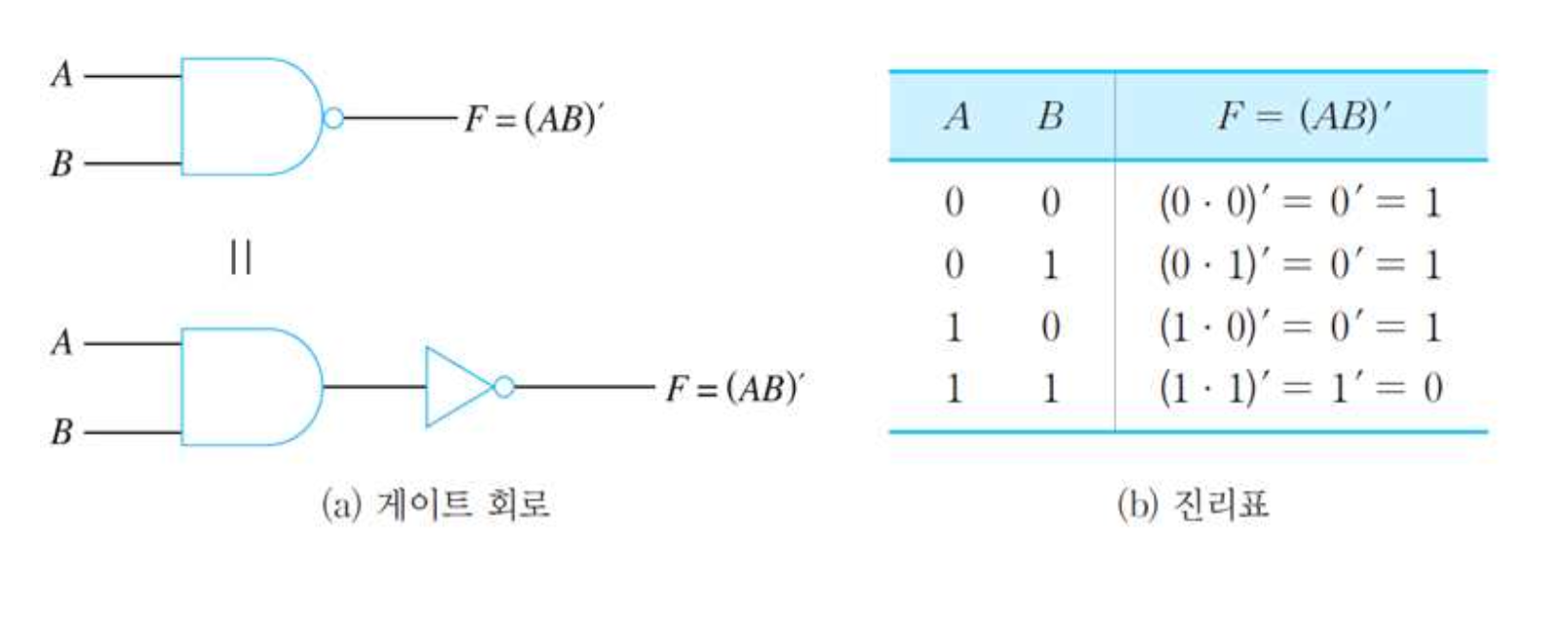
(2) NAND 함수 : F = (AB)’

• (AB = AND)
• 그뒤에 NOT을 붙임 (인버터)