디지털 공학 개론 - 부울대수의 법칙과 규칙

1. 부울대수의 법칙

1) 교환 법칙 (Commutative law)

• A + B = B + A (OR)
• AB = BA (AND)
• 증명

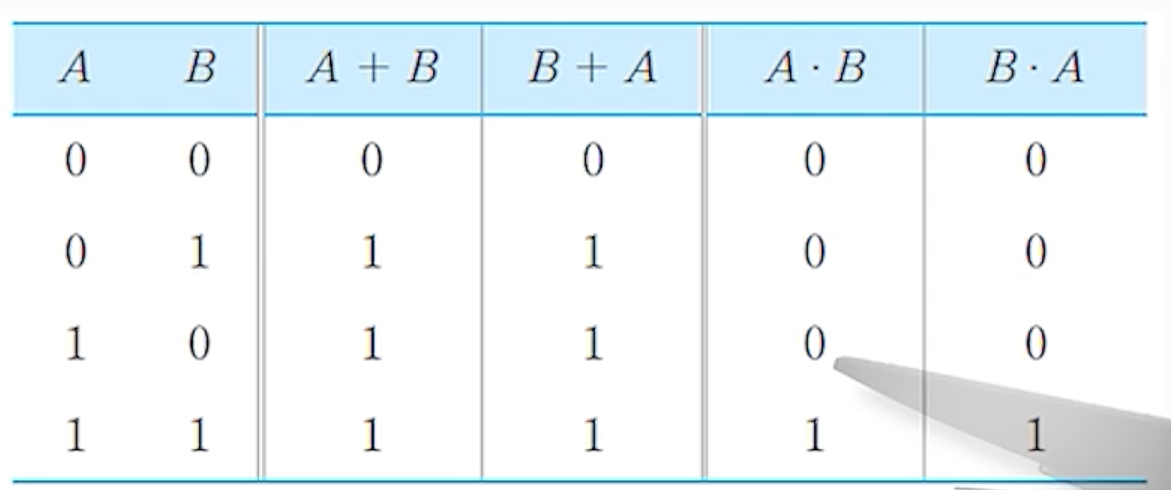
2) 결합 법칙 (Associative law)

• (A+B) + C = A + (B+C)
• A(BC) = (AB)C
• 증명

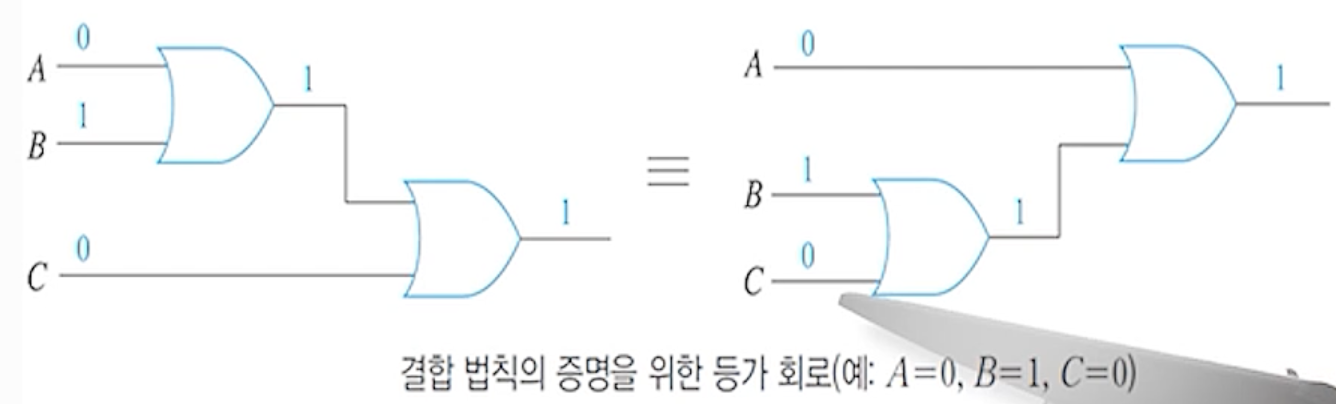
3) 분배 법칙 (Distributive law)

• A(B+C) = AB + AC
• A + BC = (A+B)(A+C)
• 증명

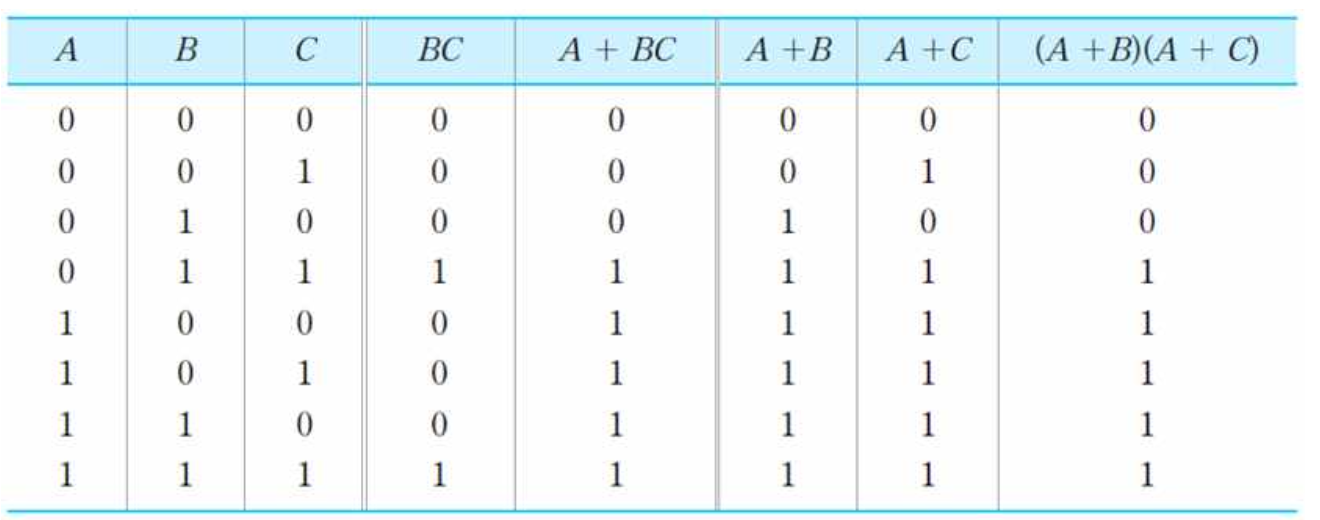
4) 팩터링(factoring) : 공통 변수의 묶음

• 예) AB + AC = A(B+C)

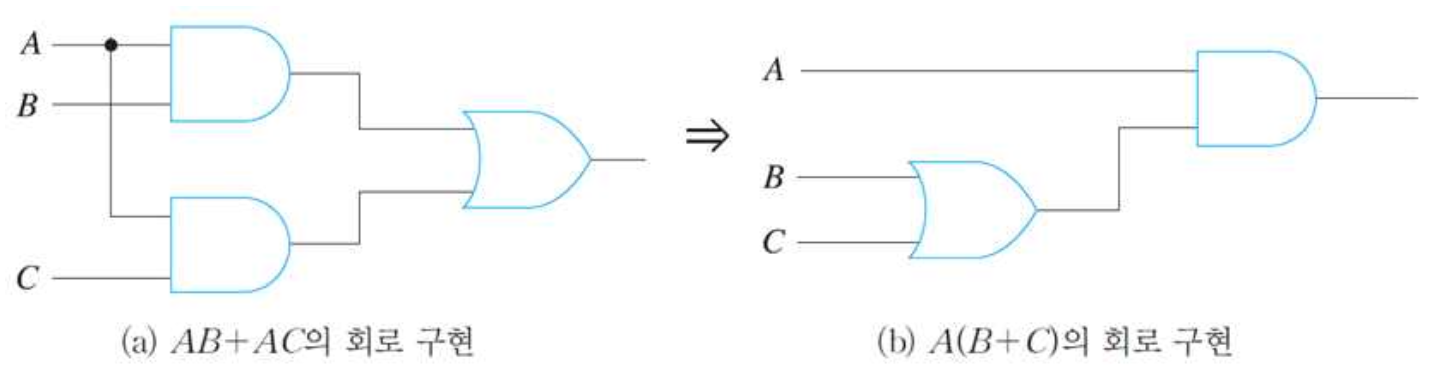
2. 부울대수의 규칙

1) (규칙 - 1) A X 0 = 0

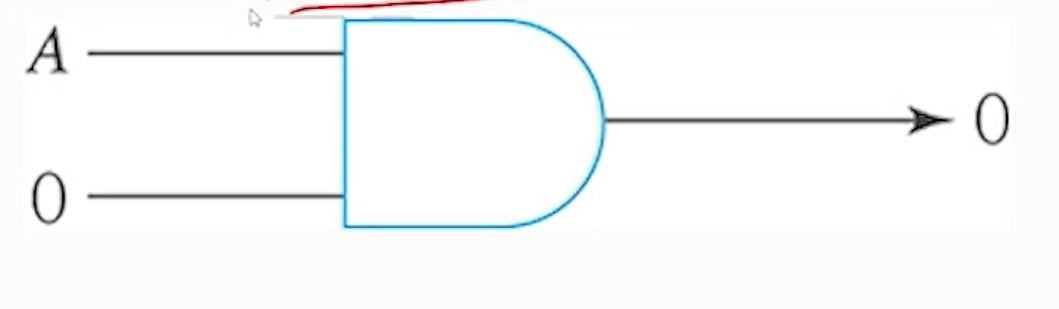
2) (규칙 - 2) A X 1 = A

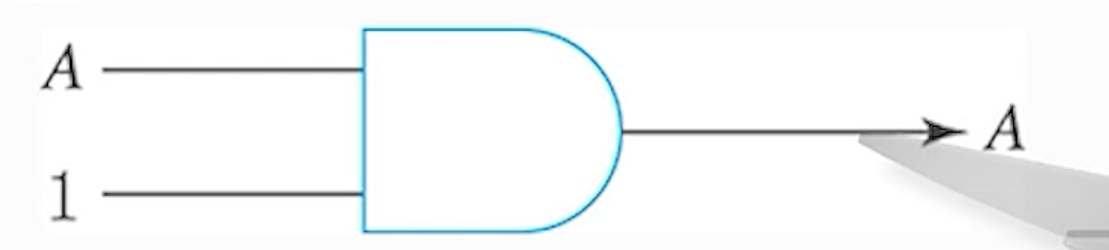
3) (규칙 - 3) A X A = A

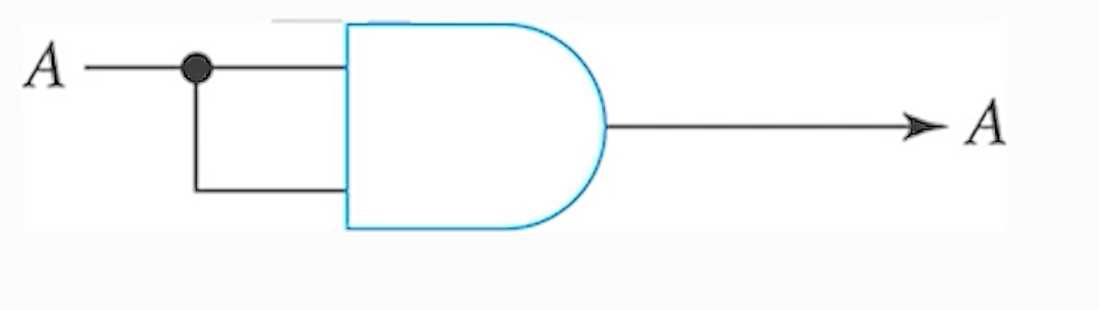
4) (규칙 - 4) A X A’ = 0

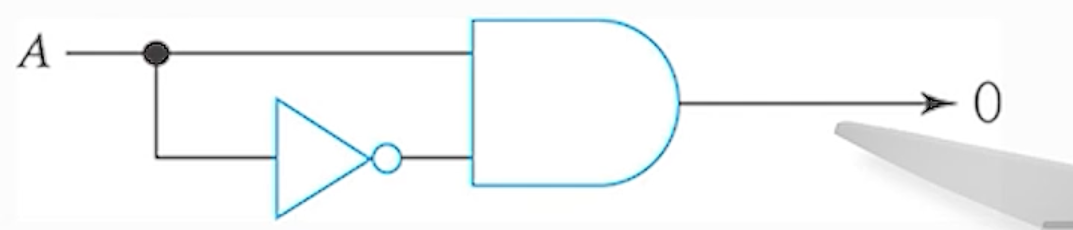
5) (규칙 - 5) A + 0 = A

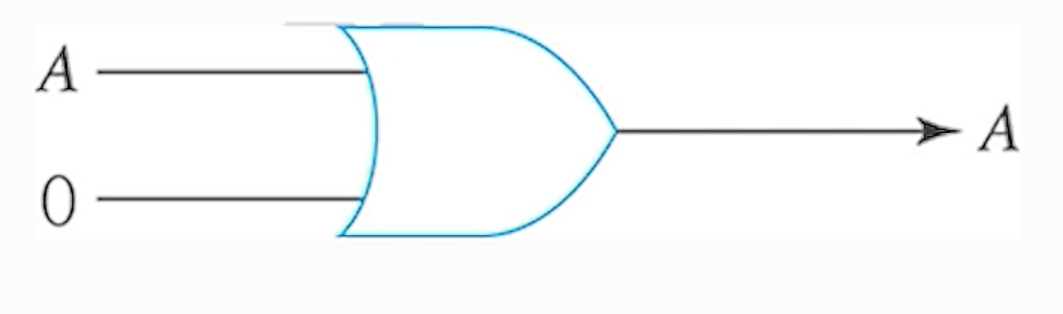
6) (규칙 - 6) A + 1 = 1

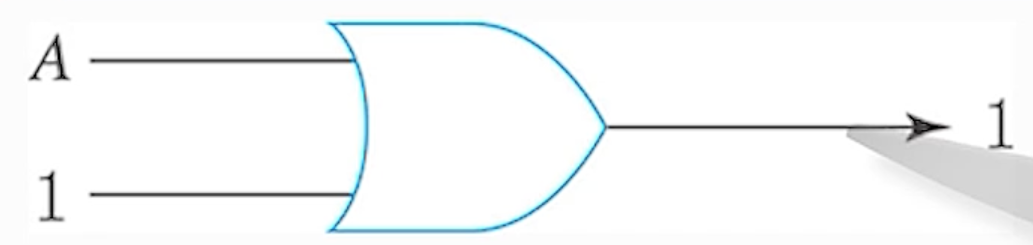
7) (규칙 - 7) A + A = A

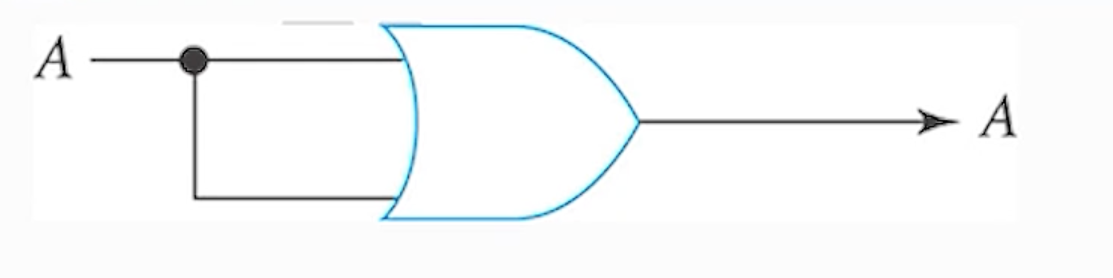
8) (규칙 - 8) A + A’ = 1

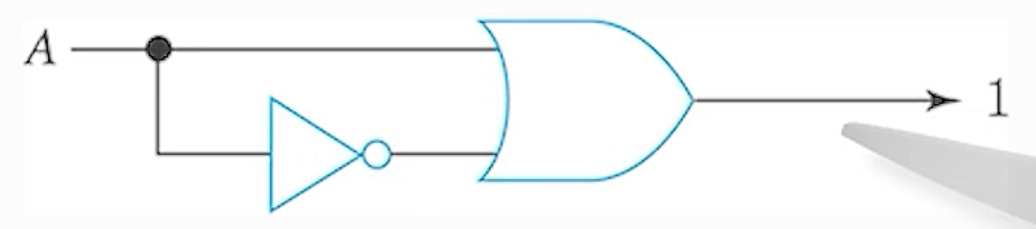
9) (규칙 - 9) A’’ = A

10) (규칙 - 10) A + AB = A

  A + AB = A(1 + B)
         = A * 1      // 규칙 6 : (1+B) = 1
         = A          // 규칙 2 : A * 1 = A

11) (규칙 - 11) A + A’B = A + B

  A + A'B = (A + A')(A + B)
          = 1 * (A + B)     // 규칙 8 : A + A' = 1
          = A + B

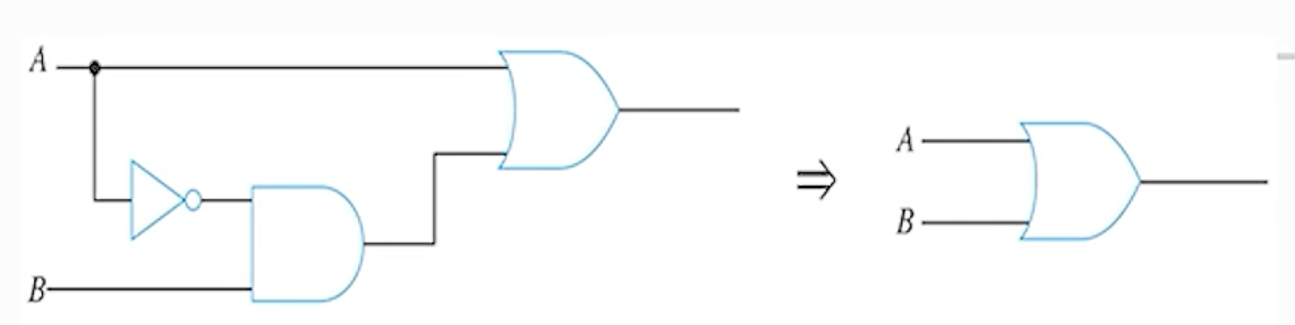
12) (규칙 - 12) (A + B)(A + C) = A + BC

  (A + B)(A + C) = AA + AC + AB + BC
                 = A + AC + AB + BC     // 규칙 3 : A * A = A
                 = A(1 + C) + AB + BC
                 = A + AB + BC          // 규칙 6 : A + 1 = 1
                 = A(1 + B) + BC
                 = A + BC               // 규칙 6 : A + 1 = 1

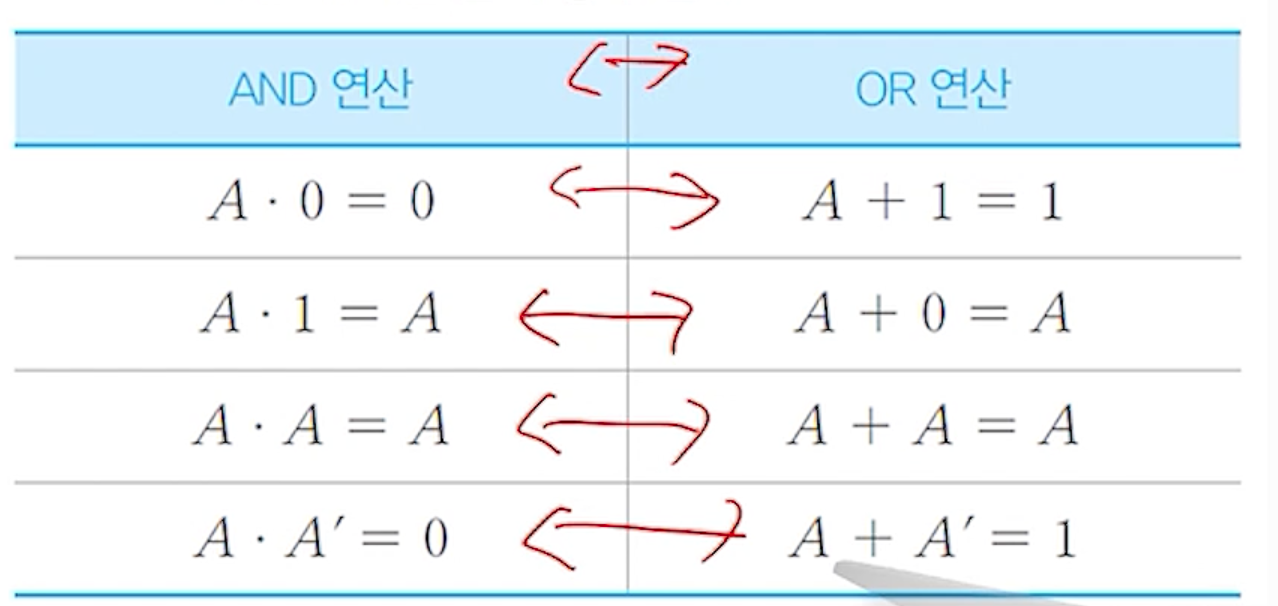
3. 쌍대성의 원리 (Principle of Duality)

• AND 연산에 관한 규칙에서 연산자 및 변수값을 반대로 바꾸면 OR 연산자 규칙이 됨
• 반대의 경우도 성립 <AND <-> OR, 1 <-> 0>