디지털 공학 개론 - 부울대수를 이용한 논리회로 분석

1. 드모르간의 정리

1) 드모르간의 정리 (DeMorgan’s theorem)

• 부울대수에서 가장 중요한 두가지 정리
• 수학자 드모르간에 의해 개발
• 부울함수의 간략화 혹은 변형에 유용하게 사용됨

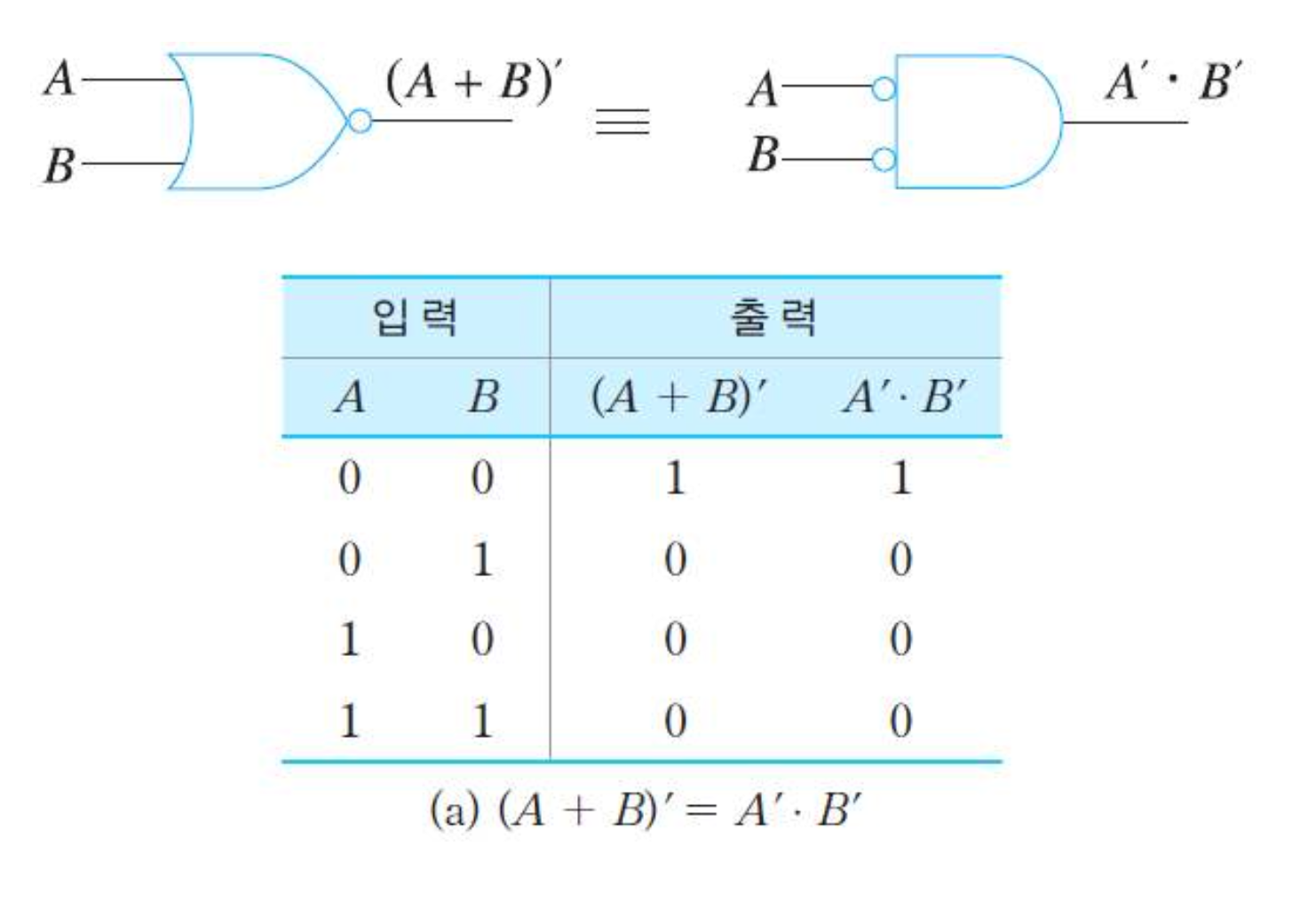
2) 정리 1

• 두 변수들 간의 합에 대한 보수는 각 변수의 보수들간의 곱과 같음

  (A+B)' = A' * B'
  (A+B+C+..)' = A' * B' * C' * ...

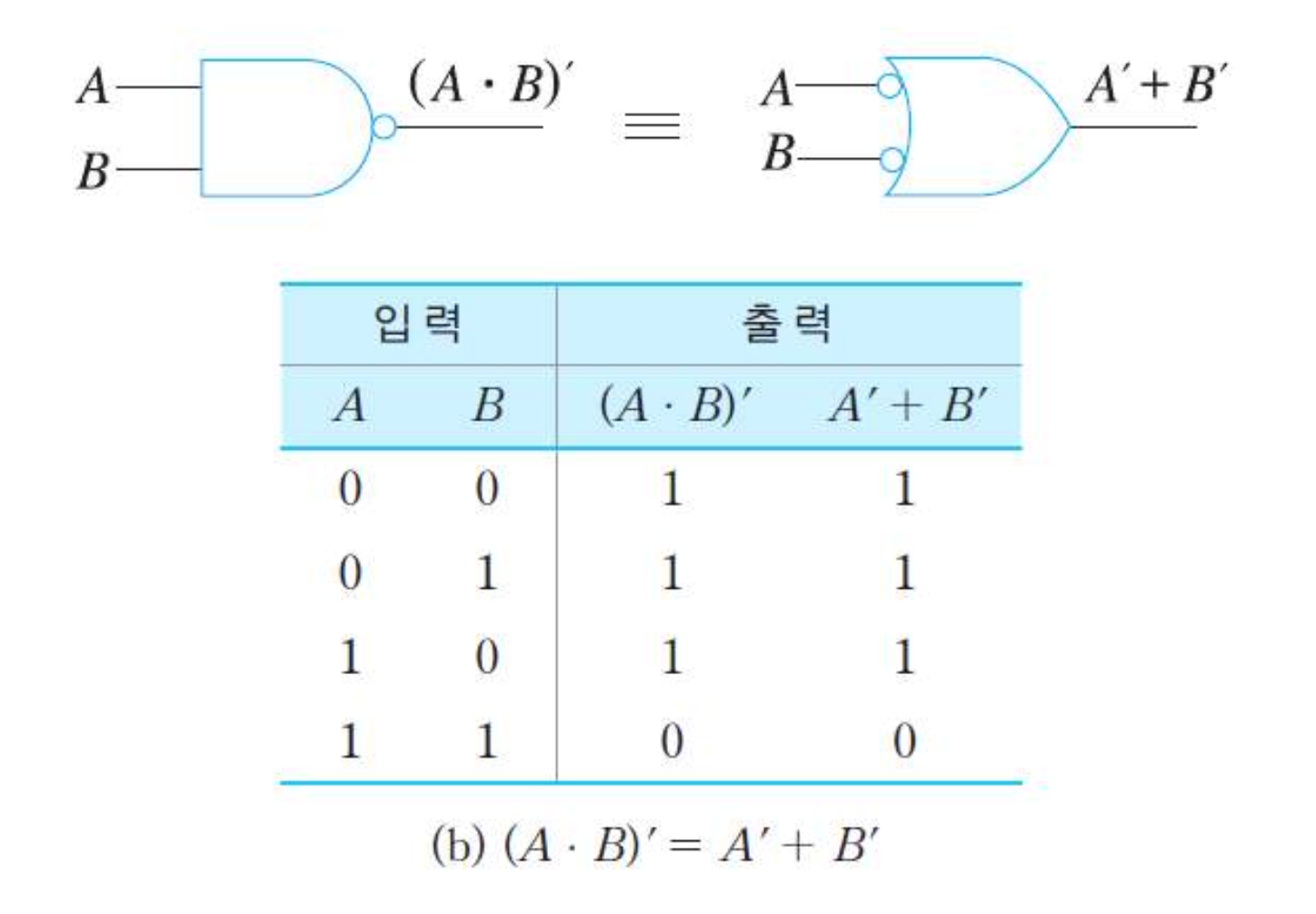
3) 정리 2

• 두 변수간의 합에 대한 보수는 각 변수의 보수들 간의 합과 같음

  (A * B)' = A' + B'
  (A * B * C * ...)' = A' + B' + C' + ...₩

2. 부울대수를 이용한 논리회로 분석

1) 분석 절차

1. 논리회로에 대한 부울함수를 유도함
2. 유도된 부울함수로부터 회로의 논리적 연산 과정을 파악함.
3. 진리표(truth table)를 작성하여 전체적인 연산 과정 및 입출력 관계를 확인함

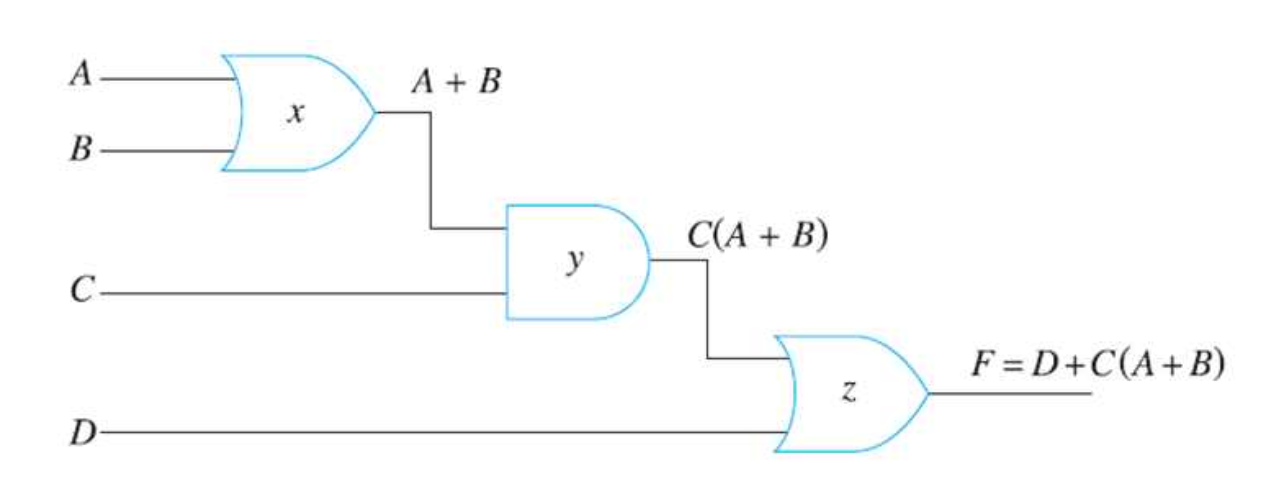
(1) 부울 함수 F = D + C(A+B)를 이용한 회로의 특성 분석 결과

• D = 1이면, 출력 F는 다른 입력 값들에 상관없이 항상 1이 됨
• D = 0일 때 C = 0이라면, F= 0이 됨
• D = 0일 때 C = 1이라면, A와 B 중의 어느 하나라도 1이면 F=1이 됨

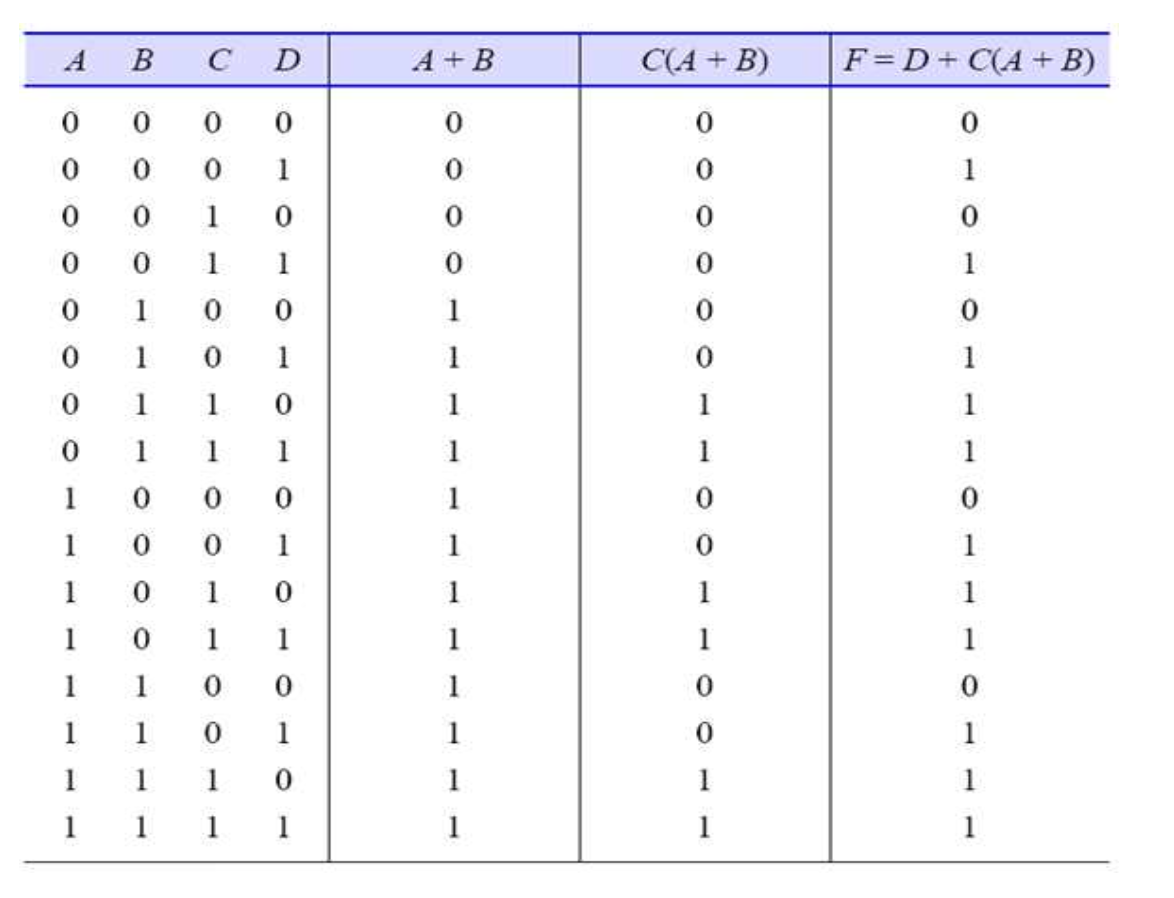
(2) 진리표를 이용한 회로 분석 (입력에 따른 연산과정과 출력)