디지털 공학 개론 - 부울대수를 이용한 논리회로의 설계
1. 부울대수를 이용한 논리회로 설계 절차
1) 설계 절차
- 설계할 회로의 기능을 나타내는 진리표를 작성함
- 진리표로부터 부울함수를 유도함
- 부울함수를 간략화 함
- 논리 게이트들을 이용하여 회로를 구성함
2) 최소항과 최대항
- 진리표로부터 부울 함수를 유도하는 방법
- 최소항(minterm) 혹은 최대항(maxterm)을 이용
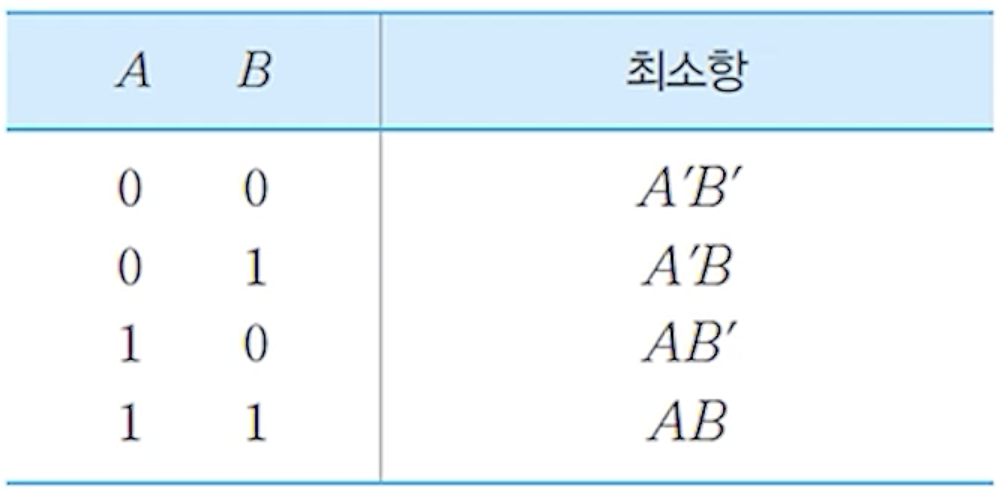
(1) 최소항 구하는 방법
- 입력값 = 1 인 변수는 정상 형(normal form)으로 표현하고
- 입력값 = 0 인 변수는 보수 형(complement form)으로 표현 후
- 변수들을 곱(product)의 형태로 표현
- 표준 곱(standard product)이라고도 부름
- 각 항은 입력변수들 간의 AND 연산 결과가 ‘1’이 되도록 표현한 결과에 해당
(2) 2- 입력변수 (A,B)에 대한 최소항
(3) 최대항 구하는 방법
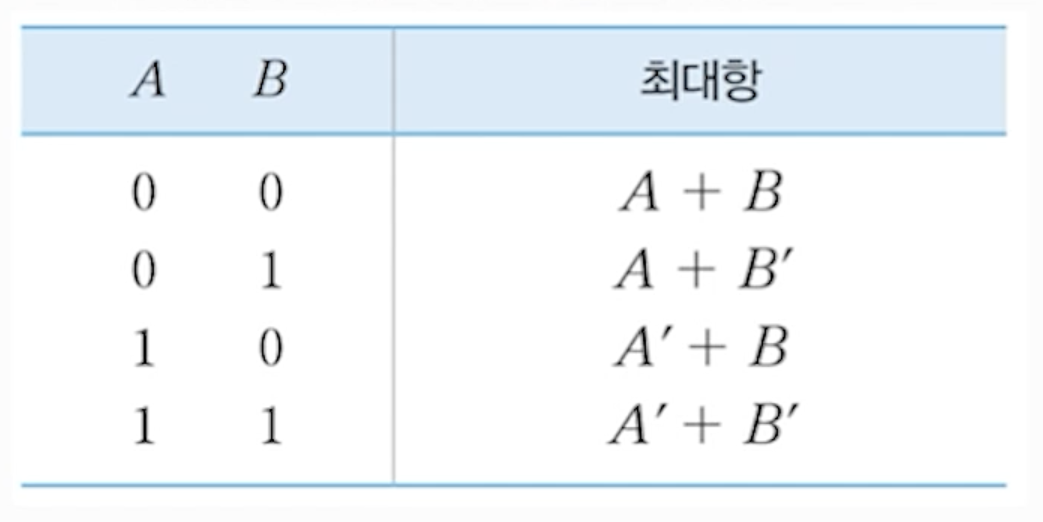
- 입력값 = 0 인 변수는 정상 형(normal form)으로 표현하고
- 입력값 = 1 인 변수는 보수 형(complement form)으로 표현 후
- 변수들을 합(sum)의 형태로 표현
- 표준 합(standard sum)이라고도 부름
- 각 항은 입력변수들 간의 OR 연산 결과가 ‘0’이 되도록 표현한 결과에 해당
(4) 2- 입력변수 (A,B)에 대한 최대항
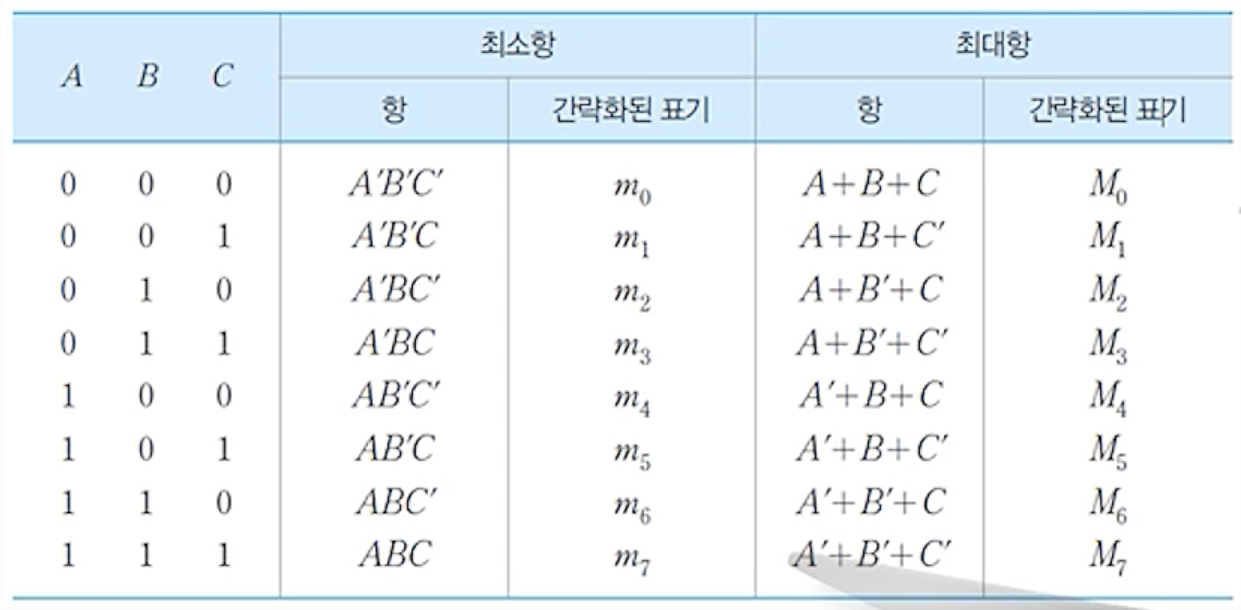
(5) 3- 변수 시스템에서의 최소항과 최대항들
2. 논리회로의 설계 사례
1) 설계 사례
(1) 설계할 회로의 기능 설정
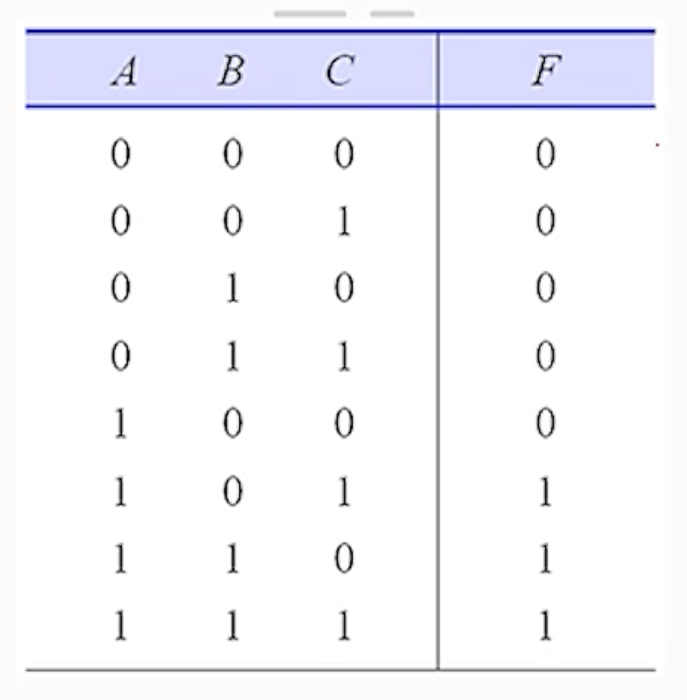
- 세 개의 입력들로 이루어지는 2진수 조합이 나타내는 10진수의 값이 0부터 4까지일 때는 출력으로 ‘0’을,
5이상인 경우에는 출력으로 ‘1’을 발생함
(2) 진리표 작성
(3) 간략화
F
= AB'C + ABC' + ABC
= AB'C + AB(C'+C)
= AB'C + AB
= A(B'C+B)
= A(B'+B)(C+B) // 분배법칙
= A(B+C)
(4) 회로 구성
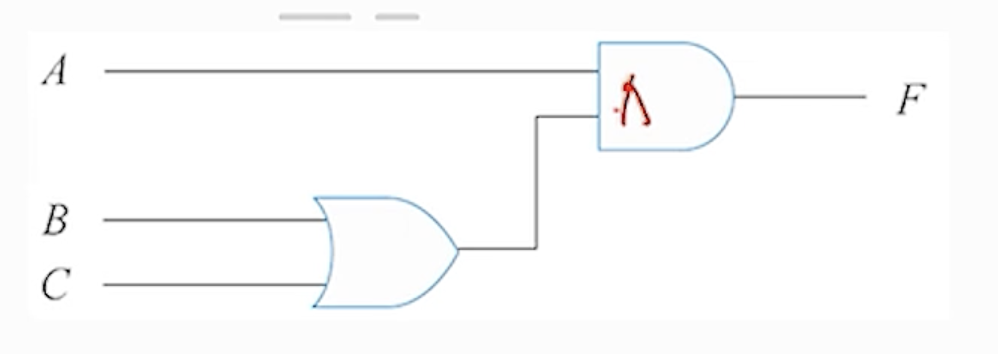






댓글남기기