디지털 공학 개론 - 표준형 부울함수의 표현

1. 혼합된 부울함수와 표준형 부울함수의 회로 비교

1) 표준형 함수

• 부울 곱으로 이루어진 항들의 합, 혹은 부울 합으로 이루어진 항들의 곱으로 표현된 함수
• 일관성있게 정리된 형태의 부울함수
• 간략화과정을 거친 후에 얻어지므로 각 항에 포함되지 않은 변수들도 있다는 것이 정규형 함수와의 차이점

2) 함수 형태 및 구현 회로 비교

• 일반형

  F(A,B,C) = A(B+C) + BC

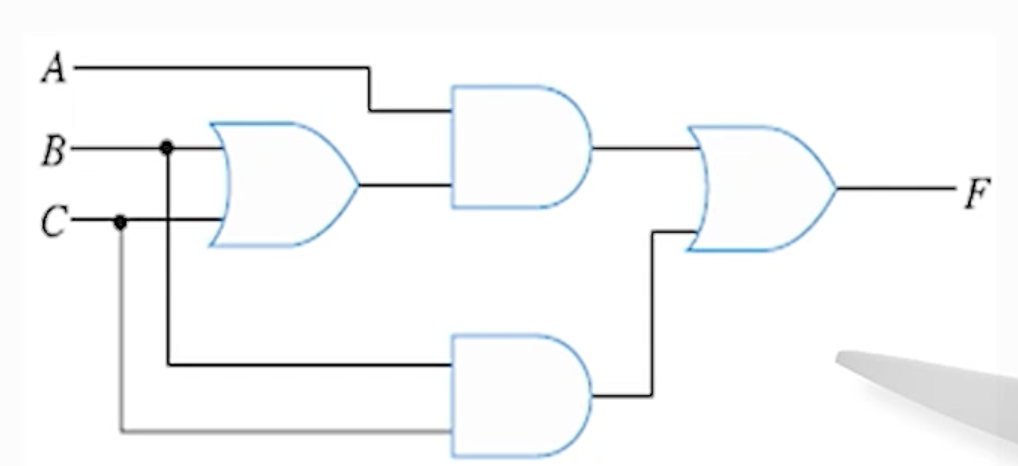
• 표준형 : 분배법칙을 이용하여 곱의 합으로 변형

  F(A,B,C) = AB + AC + BC

(1) 표준형의 장점

• 처리 시간 단축 (두 단계)
• 회로 구성의 단순화
• 이와 같은 이점때문에 부울함수를 간략화 시킨 다음에는 다음과 같은 두가지 형태들 중 어느하나로 정리하는 것이
  바람직함 (SOP, POS)

2. SOP 표현

1) 개념

• 논리적 곱으로 이루어진 두개의 이상의 항들이 부울 덧셈에 의해 합해진 형태의 부울 함수

  F(A,B,C) = A + BC + A'BC'
  F(A,B,C,D) = AB'C + BC'D' + ABCD'

2) 특징

• 항들 중의 하나 이상이 1이면, 출력 F = 1
• AND-OR 회로에 의해 구현
• 표준형으로 표현되지 않은 부울 함수를 SOP형으로 변형하는 방법 : 분배 법칙 이용

3) 정규형 SOP 표현

• SOP형 부울 함수의 각 항이 도메인(domain)내 모든 변수들을 포함한 형태의 부울 표현
• 정규형 SOP 표현이 아닌 함수의 예

  F(A,B,C,D) = A'CD + AB' + ABC'D
               ----   ----
                B     C,D - 포함되지 않은 변수들

(1) 정규형 SOP 표현으로의 변환

• 각 항들이 모든 변수들을 포함시키기 위하여 각 항에 없는 변수에대한(x+x’)을 곱한 후, 전개
• 예) F(A,B,C,D) = A’CD + AB’ + ABC’D

  A'CD = A'CD(B + B') = A'BCD + A'B'CD

  AB' = AB'(C + C') = AB'C + AB'C'
      = AB'C(D + D') = AB'C'(D + D')

      = AB'CD + AB'CD' + AB'C'D + AB'C'D'

(2) 정규형 SOP 표현의 장점

• 부울 함수의 분석을 위한 진리표 작성이 용이
• 카노프 맵의 작성이 용이 (부울 함수 간략화 과정)