디지털 공학 개론 - 표준형 부울함수의 표현

1. POS 표현

1) 개념

• 논리적 합으로 이루어진 두개 이상의 항들이 부울 곱에 의해 곱해진 형태의 부울 함수

  F(A,B,C) = A(B + C)(A' + B + C')
  F(A,B,C) = (A' + B)(A + B' + c)(A + C)
  F(A,B,C,D) = (A + B' + C)(B + C' + D')(A + C + D')

2) 특징

• 항들 중의 하나 이상이 0 이면, 출력 F = 0
• OR-AND 회로에 의해 구현
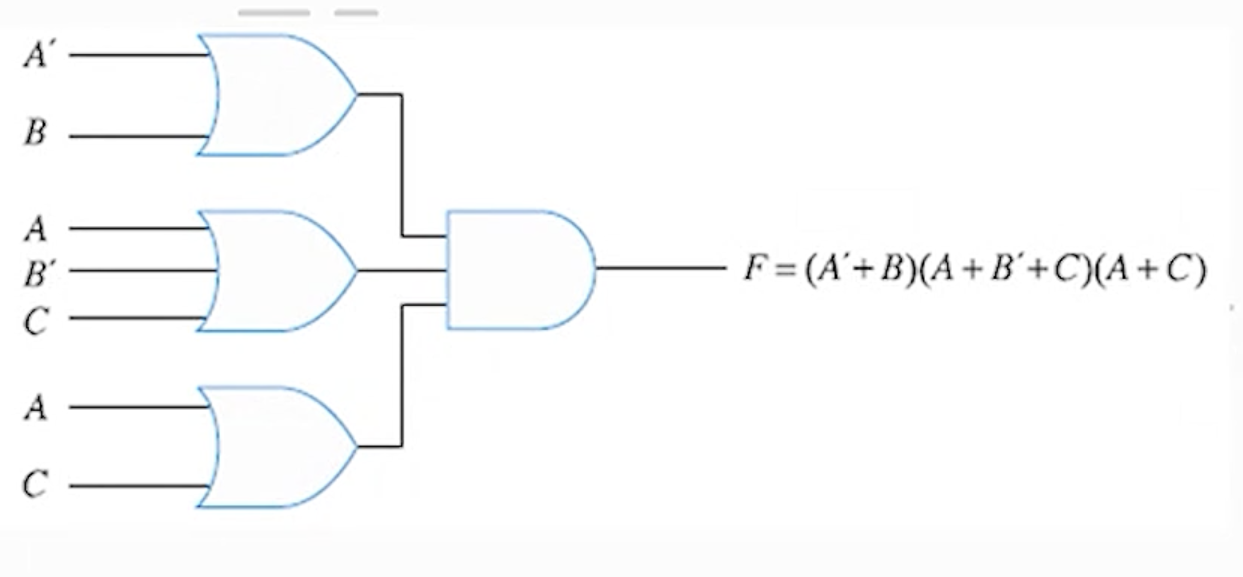
• 예) POS형 함수의 OR-AND 회로 구현 예

  F = (A' + B)(A + B' + C)(A + C)의 구현

• SOP형 부울 함수를 POS형으로 변형하는 방법
  • 분배 법칙 중의 x + yz = (x+y)(x+z)를 이용

  F
  = A'B + AC
  = (A'B + A)(A'B + C)
  = (A' + A)(B + A)(A' + C)(B + C)
  = (A + B)(A' + C)(B + C)

3) 정규형 POS

• POS형 부울 함수의 각 항이 도메인(domain) 내 모든 변수들을 포함한 형태의 부울 표현
• 정규형 POS 표현이 아닌 함수의 예

  F(A,B,C) = (A' + B)(A + B' + C)(A + C)
              ------             -------
                C                   B   - 포함되지 않은 변수들

(1) 정규형 POS 표현으로의 변환 방법

• 항에 포함되지 않은 변수에 대한 xx’을 더해준 후, 분배법칙으로 전개

  F(A,B,C) = (A + B)(A' + C)(B + C)

  <변환 과정>
  A + B  = A + B + CC' = (A + B + C)(A + B + C')

  A' + C = A' + C + BB' = (A' + B + C)(A' + B' + C)

  B + C  = B + C + AA' = (A + B + C)(A' + B + C)

  F(A,B,C) = (A + B + C)(A + B + C')(A' + B + C)(A' + B' + C)

  F = 0 이 되게 하는 입력 조합들 : 000, 001, 100, 110

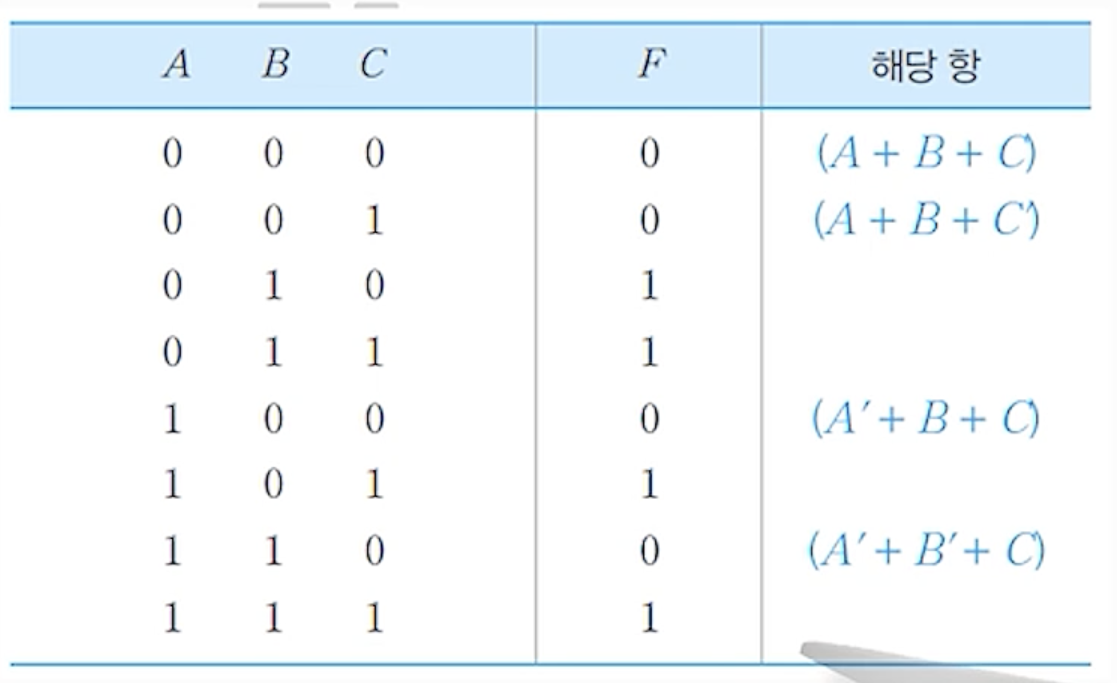
(2) 진리표 작성 방법

• F = 0 이 되게 하는 입력 조합들 (000, 001, 100, 110)에 대응되는 출력을 ‘0’으로 표시하고, 나머지는
  ‘1’로 표시

2. 정규형 SOP표현과 POS표현간의 변환

1) 정규형 SOP -> 정규형 POS 표현 변환 절차

• 어느 한 표현에 존재하는 항들을 나타내는 2진수 입력
• 조합들이 다른 표현에는 존재하지 않는다는 성질을 이용

(1) 절차

1. SOP 형으로 표현된 부울 함수에 포함된 항들에 대한 2진수 조합들을 나열
2. 1번 결과에 포함되지 않은 2진수 조합들을 찾음
3. 2번 결과로 나타난 2진수 조합들에 대한 POS 표현을 구함

2) 정규형 POS -> 정규형 SOP 표현으로 변환하는 방법

• 함수가 ‘0’이 되게 해주는 입력조합들을 구한 후, 포함되지 않은 입력 조합들을 찾아서 SOP 표현을 유도