디지털 공학 개론 - 카르노맵을 이용한 부울함수의 간략화

1. 카르노맵이란?

1) 부울함수의 간략화

• 회로구현의 효율성 향상을 위해 필요
• 회로의 복잡도를 낮추고 사용되는 부품의 수를 줄임
• 회로구현에 필요한 공간, 비용 절감 및 처리기간의 단축

(1) 카르노맵

• 부울 대수를 효과적이고 체계적으로 간략화시키기 위해 개발

2) 카르노맵 (Karnaugh map)

• 카노프팹, 카르노프앱이라고도 불리움
• 네모꼴의 모눈으로 구성된 도면
• 입력 변수들에 대한 조합 수 만큼의 셀들로 구성된 2차원ㅂ ㅐ열
• 인접해 있는 1(혹은 9)들을 2N개 단위의 그룹으로 묶고, 정해진 규칙에 따라 변수를 제거
• 3-변수, 4-변수 및 5-변수 부울 함수들에 대하여 적용 가능
• 그 이상의 변수 함수들에 대해서는 Quine-McClushy 방법 사용

2. 3변수 카르노맵과 4변수 카르노맵

1) 3변수 카르노맵

• 3 - 변수 부울함수에 대한 카르노 맵 : 2의 3승(8개) 셀들로 이루어진 2-차원 배열로 구성
• 예 ) F(A,B,C)에 대한 카르노 맵

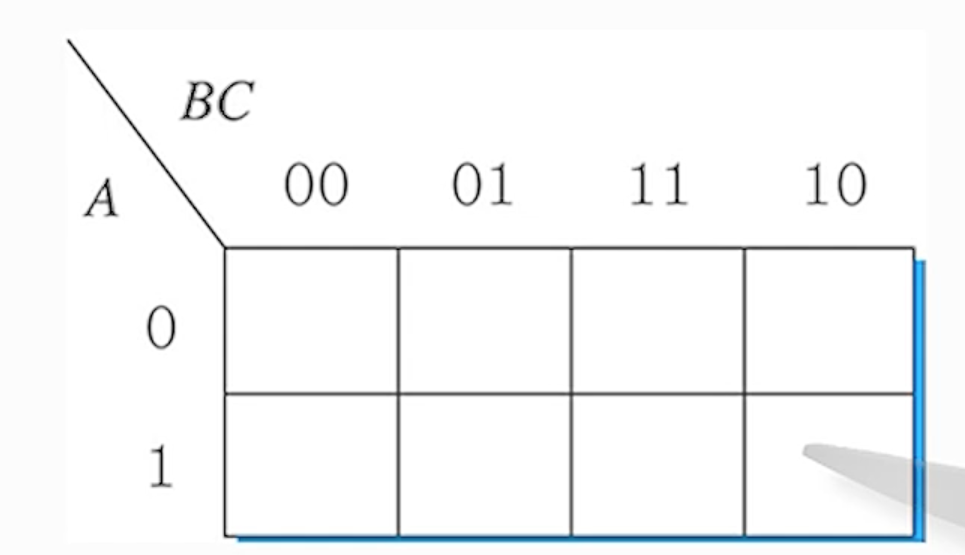
2) 3-변수 카르노 맵의 셀 배열

(1) 각 셀에 대응되는 2진수 들

• 각 조합에 대한 출력 값을 해당 셀에 기록

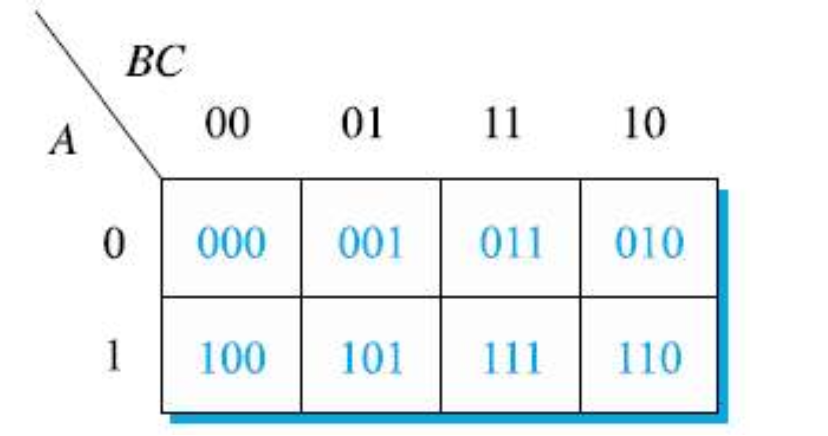
(2) 각 셀에 대응되는 최소항들

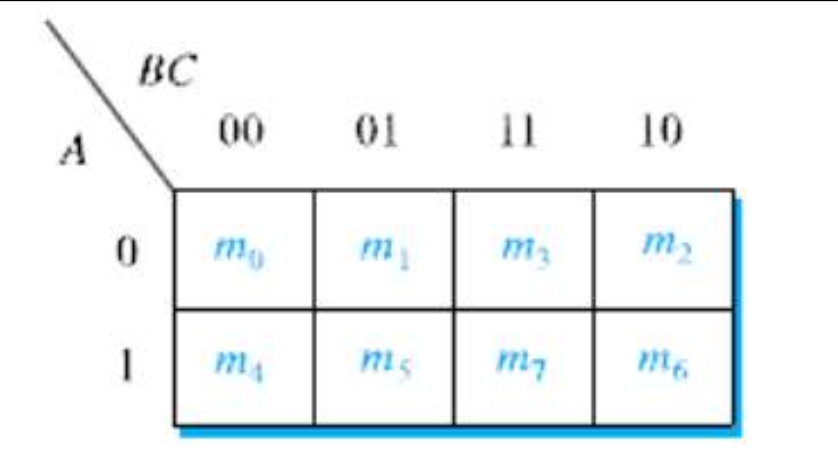
(3) 예) 진리표로부터 3-변수 카르노맵 작성

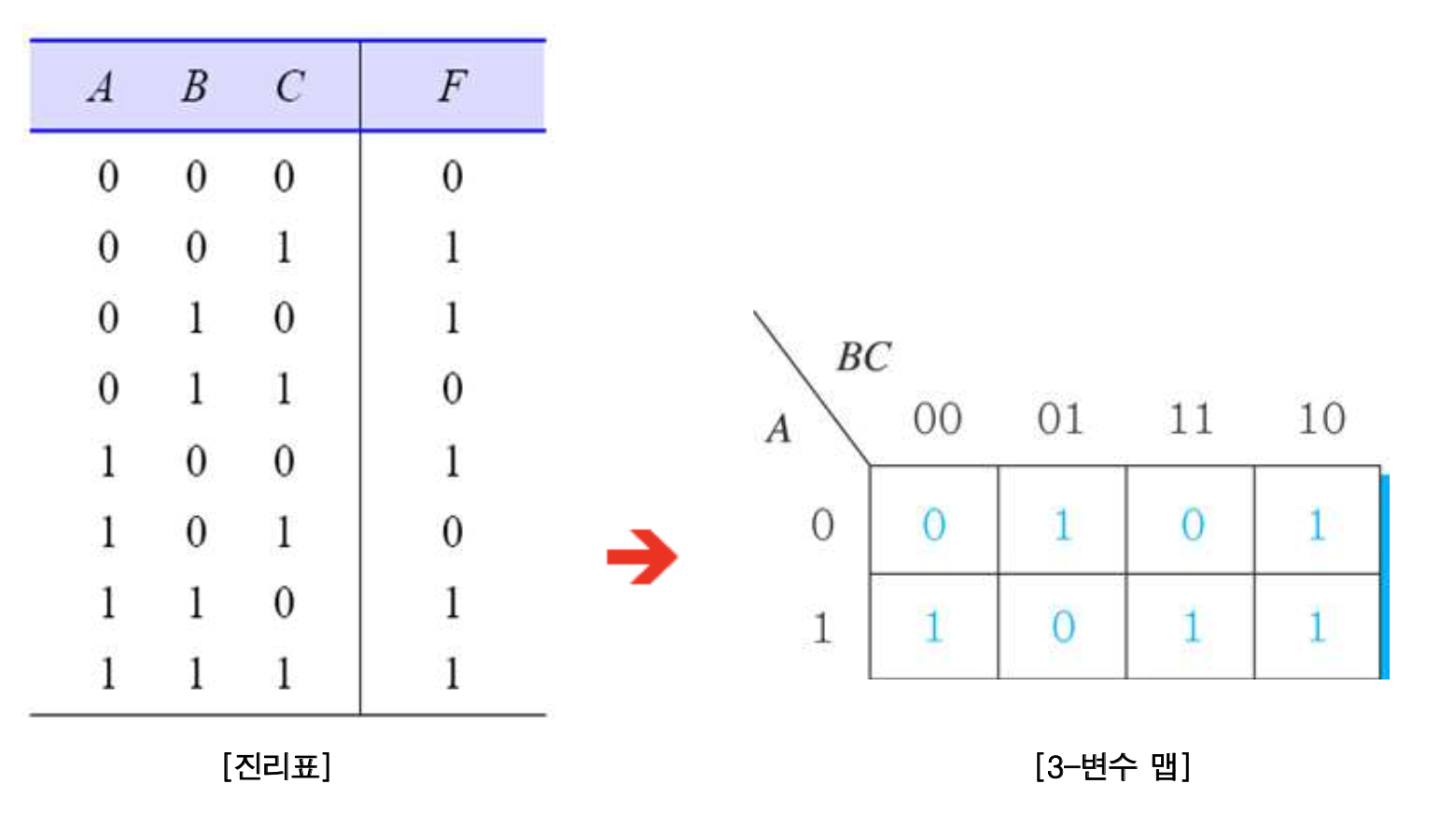
3) SOP형 부울함수에 대한 카르노 맵 작성 방법

• 정규형 SOP 표현으로 변형
• 함수를 구성하는 각 항에 대응되는 셀을 ‘1’로 채움

 F(A,B,C) = A'B'C' + BC'
          = A'B'C' + (A'+A)BC'
          = A'B'C' + A'BC' + ABC'
             000      010    110

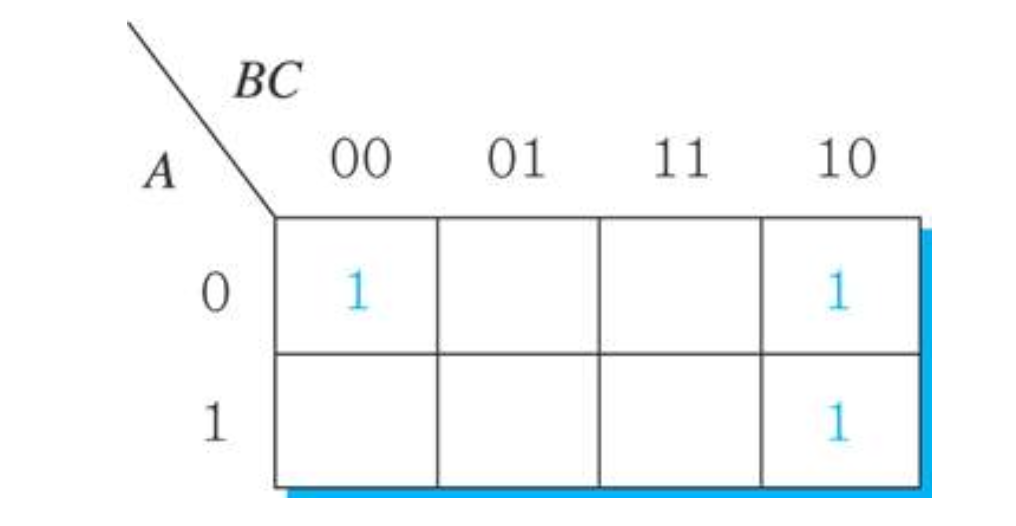
4) 4-변수 카르노 맵

• 16개(4x4) 셀로 구성
• 작성 예

  F(A,B,C,D) = A'B'C'D + ABC'D + A'BCD'
                0000      1101    0110

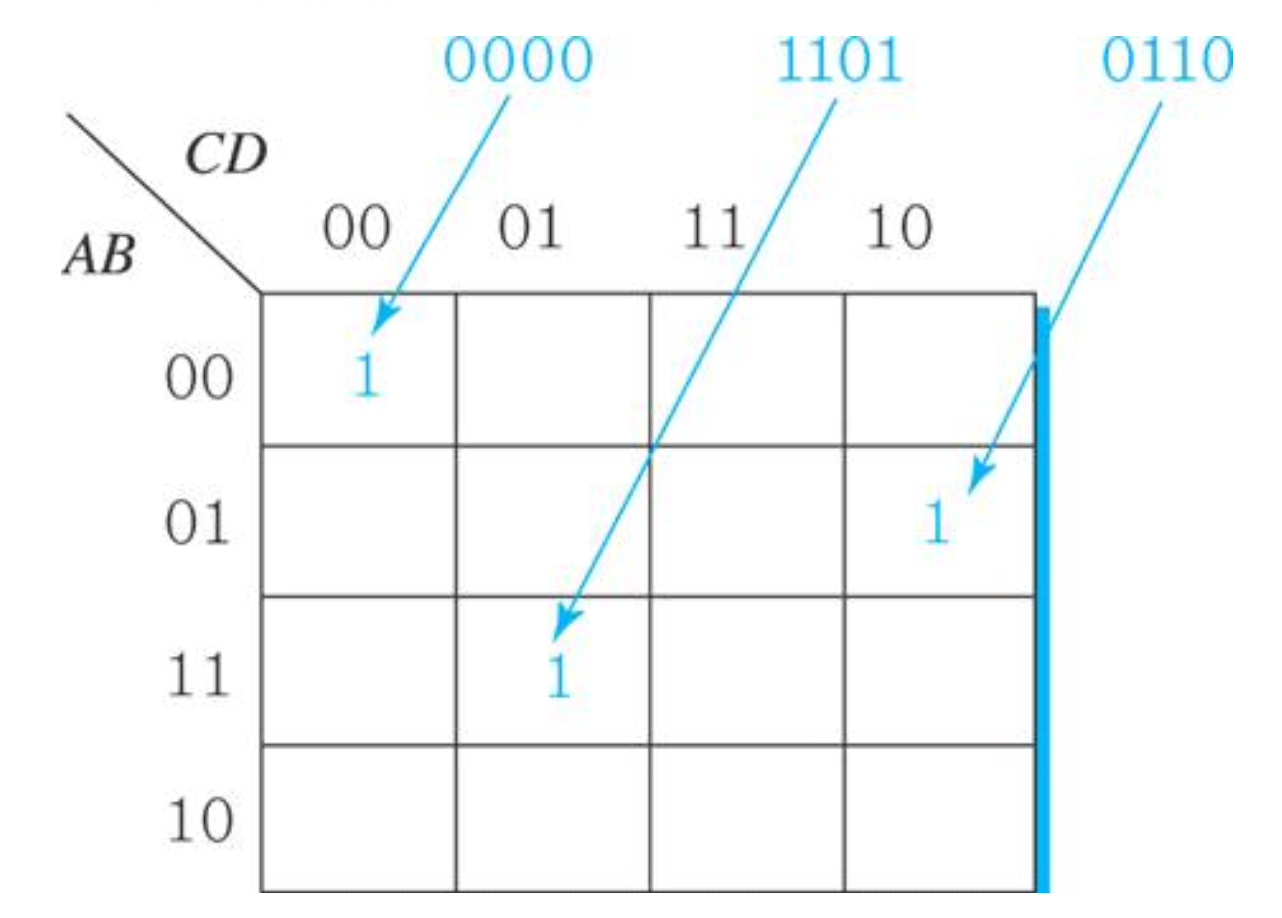
5) 정규형이 아닌 부울 함수에 대한 카르노맵 작성

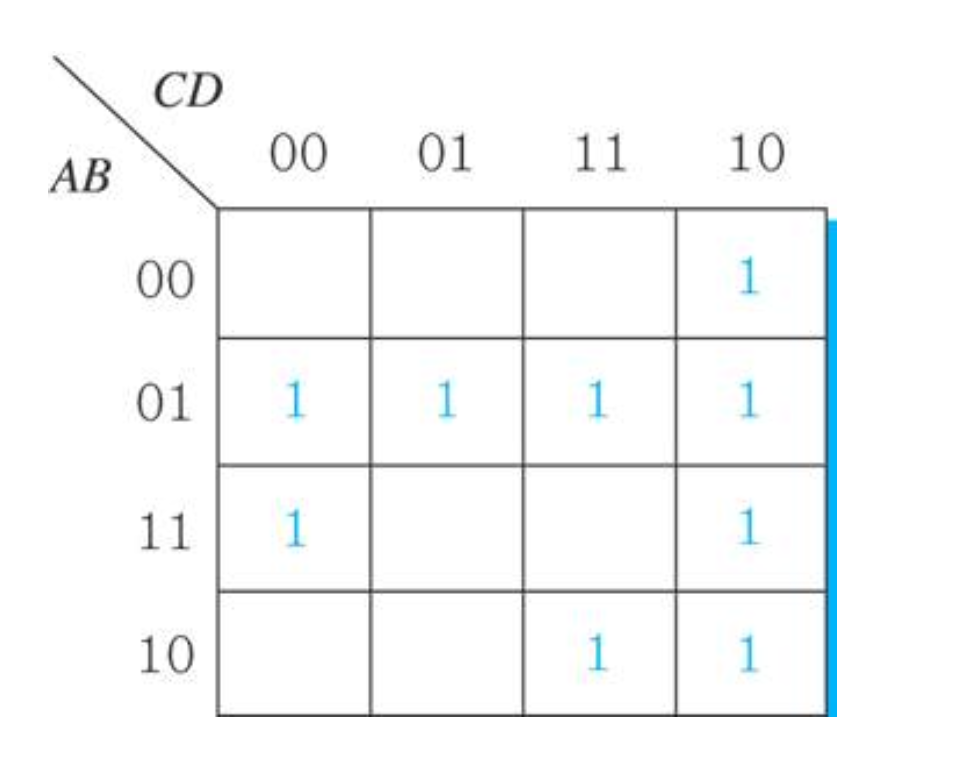
  - F(A,B,C,D) = A'B + CD' + AB'C + BCD' + ABC'D'
                0100  0010   1010   0110   1100
                0101  0110   1011   1110
                0110  1010   0111   1110