디지털 공학 개론 - 셀 인접성을 이용한 간략화

1. 3변수 카르노맵의 간략화

1) 카르노맵을 이용한 간략화의 기본 원리

• 셀들 간의 인접성관계 이용
• 인접 : 카노프 맵에서 바로 옆 혹은 위/아래에 위치
• 인접한 셀들의 최소항들 간의 특징 : 단 한 개의 변수 값만 서로 다름
• 예) 3-변수 카르노 맵에서 인접한 셀들은 한 비트만 서로 다른 값을 가짐

  000 ↔ 001, 001 ↔ 011, 011 ↔ 010 등

2) 3-변수 카르노 맵에서의 인접 관계

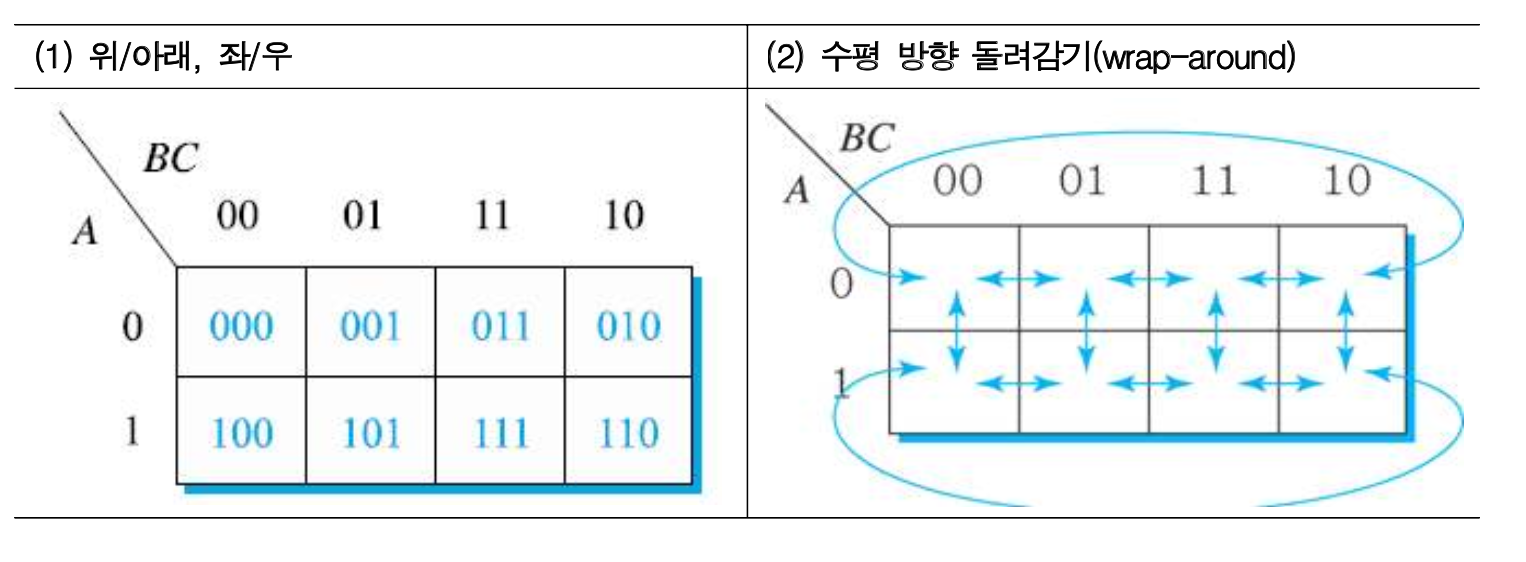
3) 셀의 묶음을 이용한 변수 제거 방법

• 1을 가진 셀들 중에서 인접한 것 들을 하나의 그룹 으로 묶음
• 단, 그룹 내 1의 개수는 2n개 단위

(1) 변수의 제거

• 묶음 그룹에 해당하는 변수들 중에서 비트값이 서로 다른 변수는 제거함
• (아래 예의 경우, 변수 B 제거)

(2) 간략화 된 항 표현

• 비트값이 같은 변수의 값이 0 이면 해당 변수를 보수형으로, 1 이면 정상형으로 표현한 최소항을
  각 그룹 당 한 개씩 구함
• 예) F(A,B,C) = A’B’C + A’BC 의 간략화

  - F(A,B,C) = A'B'C + A'BC
             = A'C(B'+B)  // 변수 B 제거 (B'+B = 1)
             = A'C

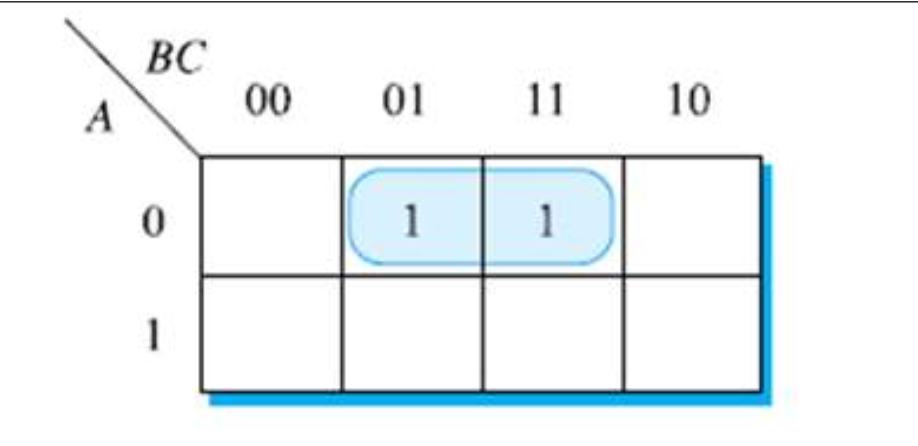
• → A’C <각 묶음 당, 한 개 항씩>
• 간략화 요령: 묶음 그룹에 관련된 변수들 중에서 그 값이 같지않은 변수를 제거
• (위의경우,수직 방향 : A=0 , 수평방향 (01,11) : B = 0&1 , C=1) ‘B’제거
• 한 그룹으로 묶을 수 있는 1의 개수 = 2n 개 (2개, 4개, 8개 혹은 16개)

2. 4변수 카르노맵의 간략화

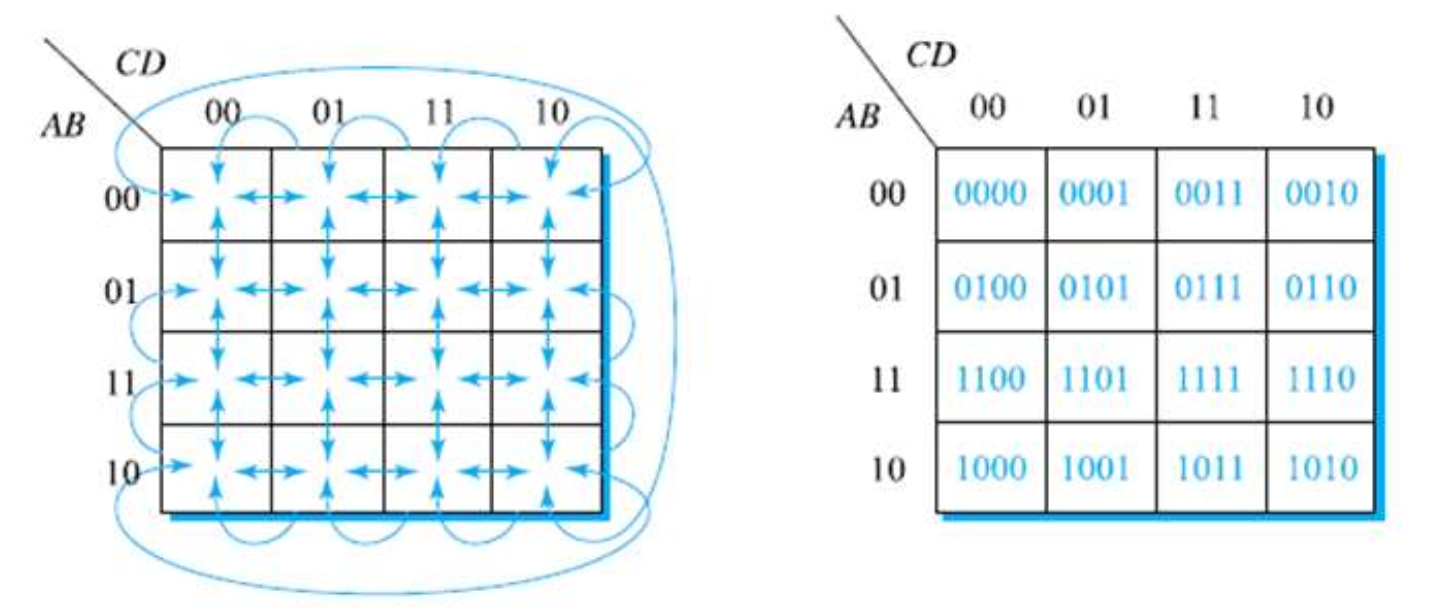
1) 4-변수 카노프 맵에서의 인접관계

• 인접한 셀들에 대한 2진수 표현은 한 비트만 서로 다름
• 인접해 있는 셀들을 2n(2,4,6,8)개 단위로만 묶을 수 있음
• 3변수와 마찬가지로 돌려감기로 묶을 수 있음
• 대각선방향으로 위치한 셀들은 서로 인접한 것으로 보지 않음

  F(A,B,C,D) = ∑(0,1,6,7,14,15) → A'B'C' + BC

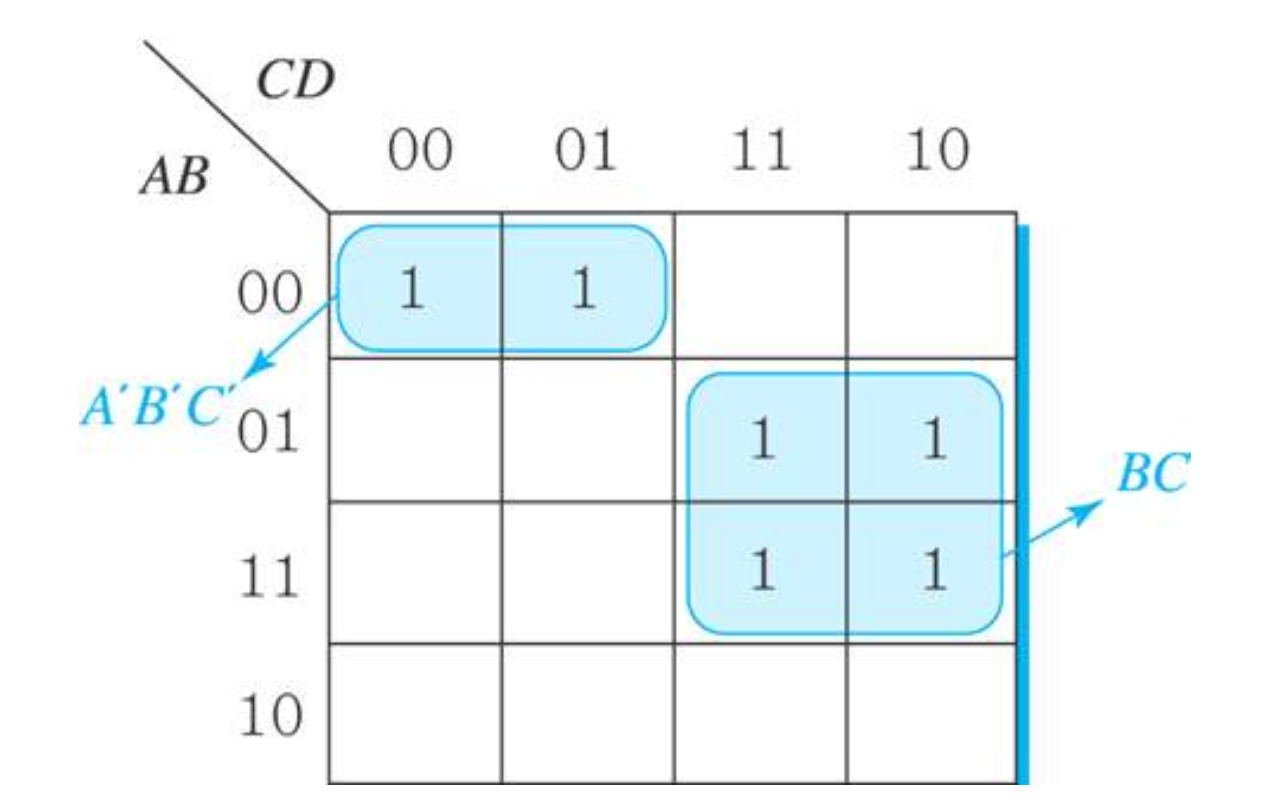
(1) 돌려감기 및 간략화의 예

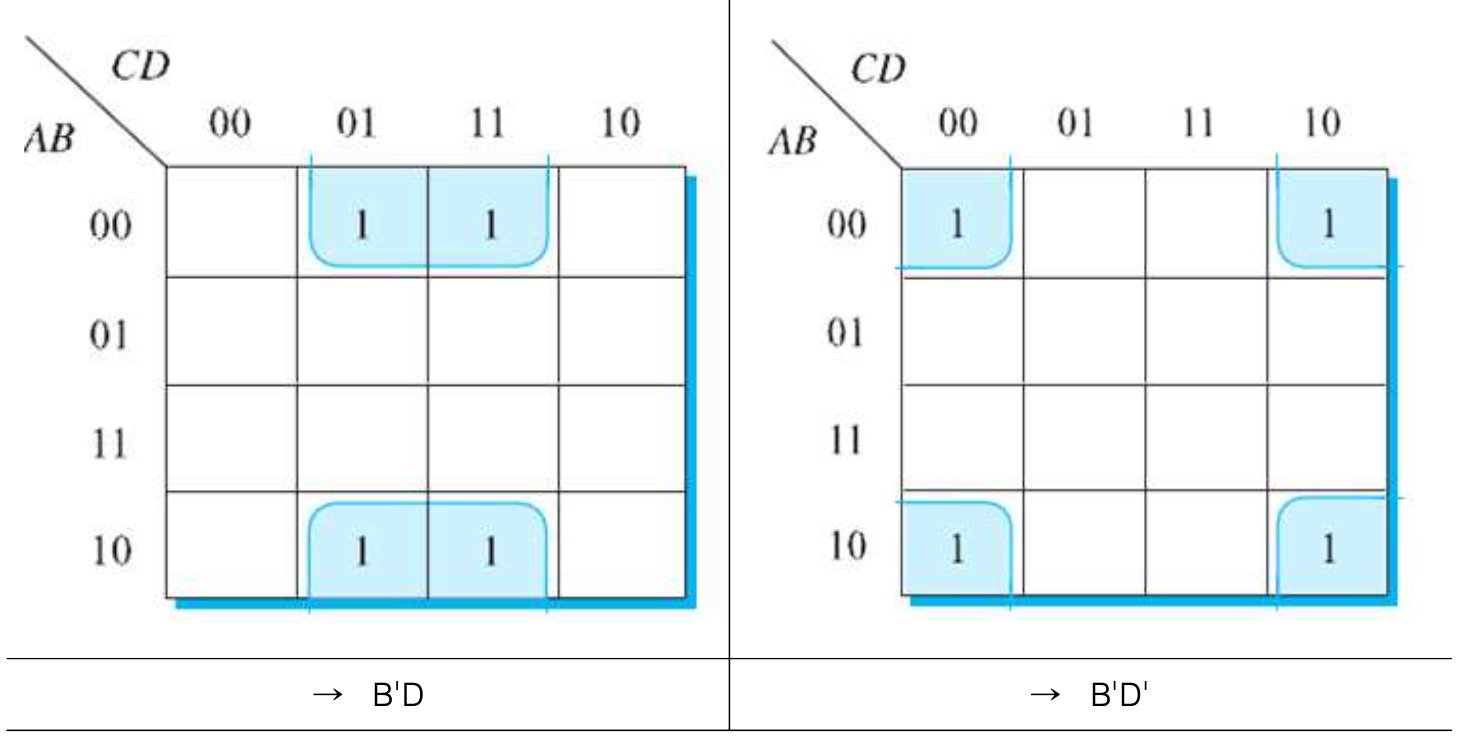
2) 4변수 카르노맵의 묶음 및 간략화

• 1의 개수가 8개인 경우의 묶음 및 간략화의 예

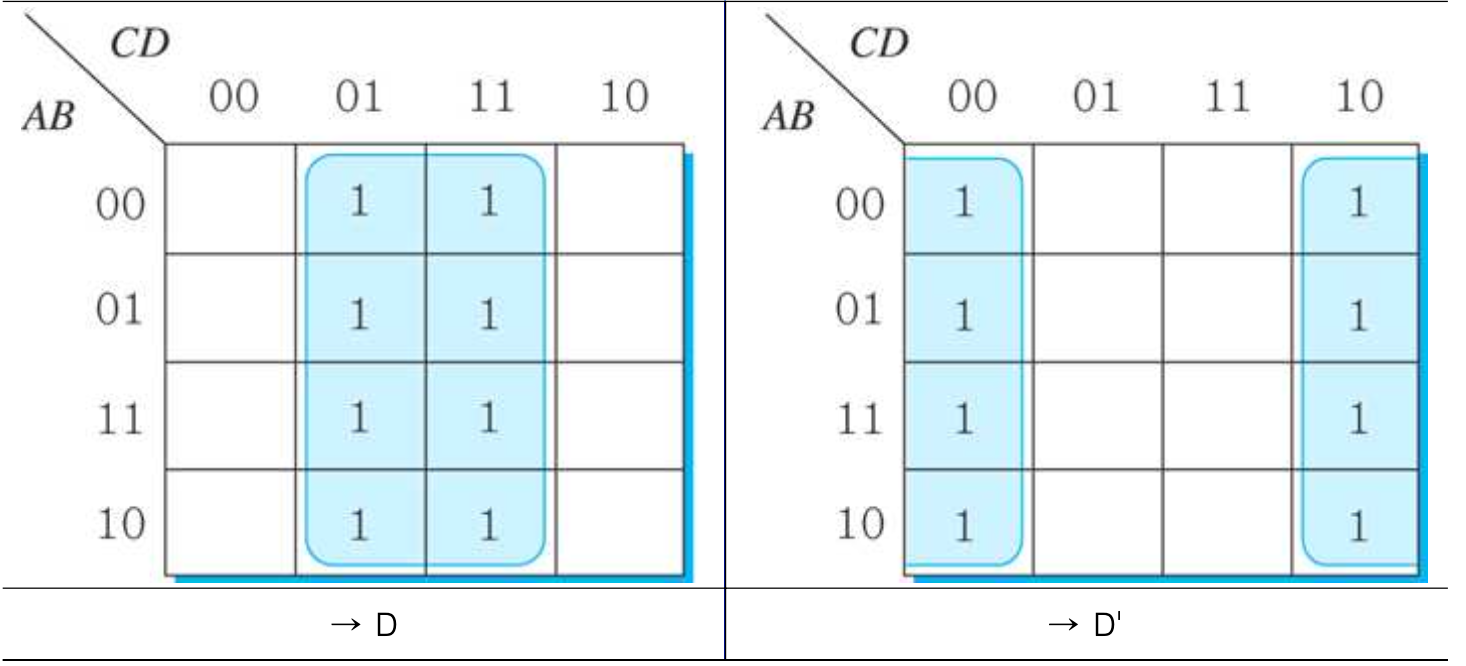
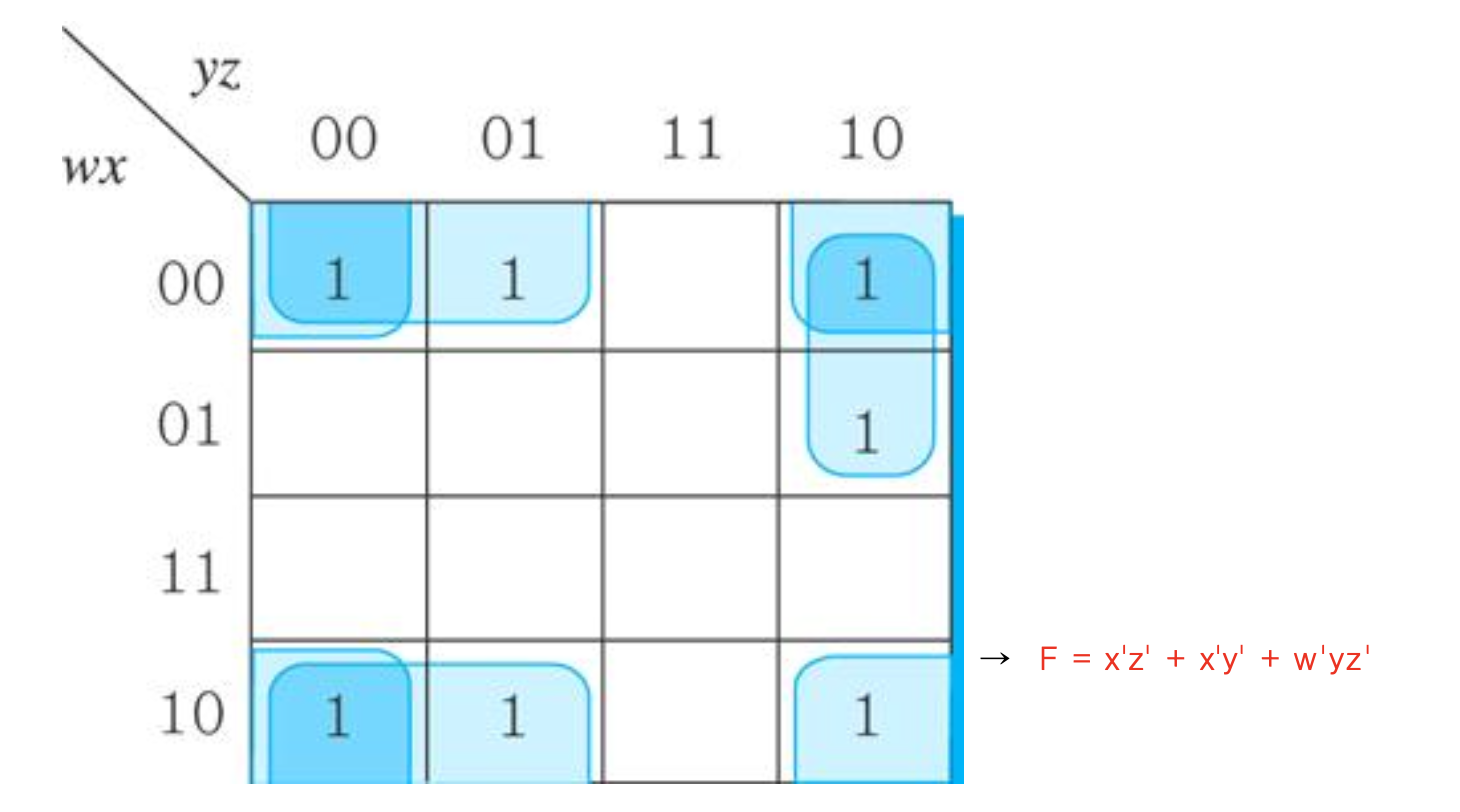
  예) F(w,x,y,z) = w'x'y' + wx'y' + x'yz' + w'xyz'
                  0000     1000    0010     0110
                  0001     1001    1010