디지털 공학 개론 - Prime implicant(주항목)

1. Prime implicant

1) 카르노맵을 사용한 부울함수의 간략화

• 부울함수를 간략화 시키기 위해서는 모든 최소항들(1로 표시된 셀들)을 가능한 한 어떤 묶음 그룹에든 포함시켜야 함
• 묶음그룹은 가능한 크게 만들어야 함
• 항의 수를 줄이기 위해 묶음그룹의 수는 최소화 해야 함
• 1로 표시된 셀이 여러 그룹에 중복적으로 포함되는 경우 부울함수의 간략화 결과가 여러 가지로 나타날 수 있음

2) Prime implicant

• 카르노 맵에서 가능한 한 많은 수의 셀들이 포함되도록 묶은 모든 그룹들에 의해 얻어진 항들
• 주항목 : 콰인-맥클러스키법(Quine-McCluskey method)에 의해 논리식을 간단하게 했을 때,
  더 이상 간단히 되지 않는 항목

  예) F(A,B,C,D) = ∑(0,1,2,4,5,6,10,11,14,15)

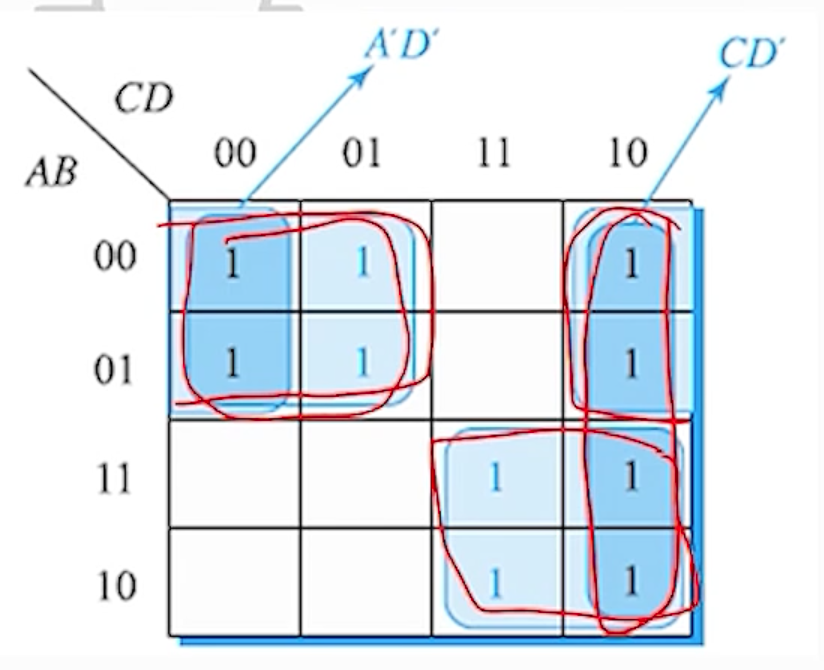
• 카르노 맵에서 묶을 수 있는 모든 그룹을 표시한 결과
• 즉, 모든 prime implicant들이 표시된 맵

2. Essential Prime implicant

1) Essential Prime implicant

• 단 하나의 묶음 그룹에만 포함된 셀을 가진 그룹에 의해 얻어짐
• 어떠한 Prime implicant에 의해서도 커버되지 않는 논리곱을 하나이상 포함하는 Prime implicant

2) Prime implicant들과 essential prime implicant의 구분

  예) F(A,B,C,D) = ∑(0,1,2,4,5,6,10,11,14,15)

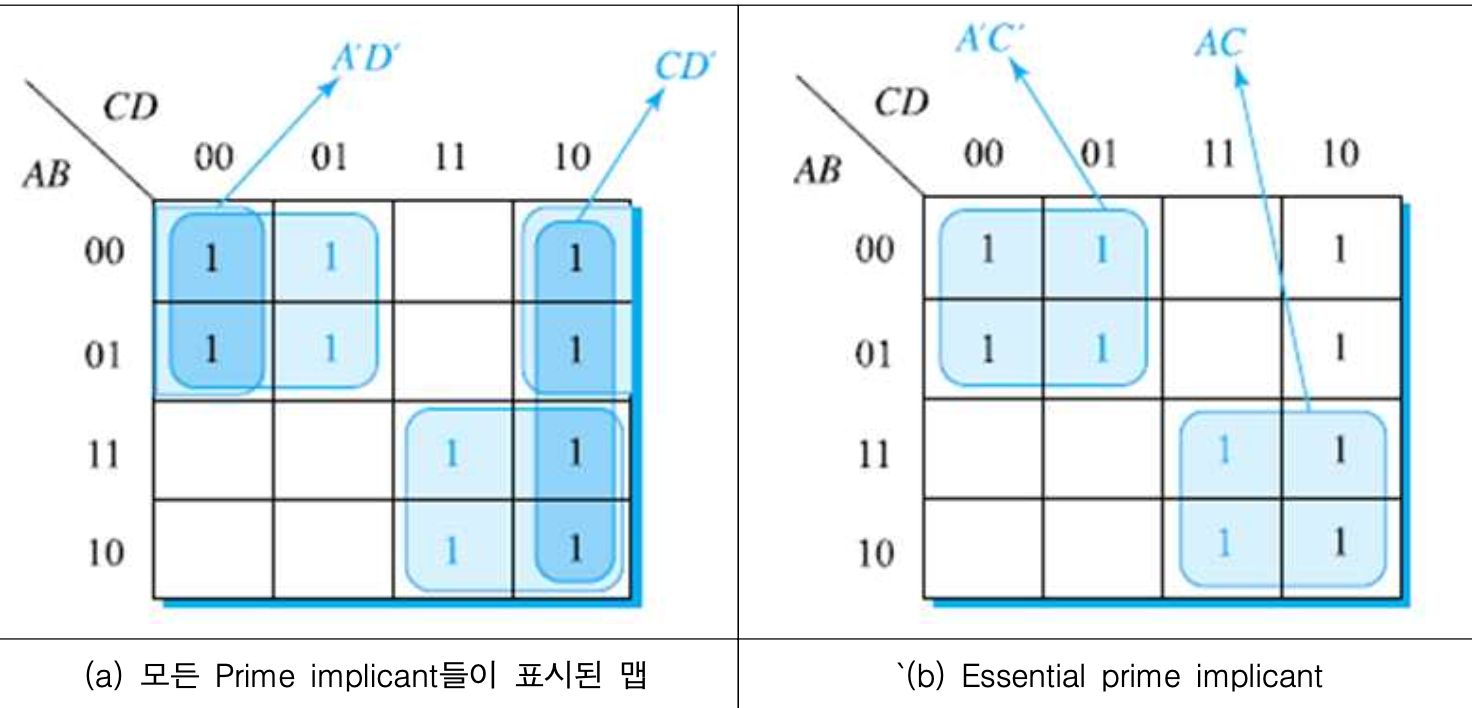
• Prime implicants : A’D’, CD’
• Essential Prime implicants : A’C’, AC
• 우측 상단의 두 개의 ‘1’들을 중복적으로 묶은 두 개의 묶음 그룹들로부터 얻어진 항 들이므로,
  둘 중의 하나만 함수에 포함되어야 함

  간략하된 부울함수

  F = A'C' + AC + A'D'
  F = A'C' + AC + CD'

3) 예제

• 다음 부울 표현에 대한 카르노맵을 작성하여 Essentional prime implicant들과
  Prime implicant들을 구하고 얻을 수 있는 간략화된 부울식을 모두 나열해보자

  예) F(w,x,y,z) = ∑(0,1,2,3,5,7,8,9,10,13,15)

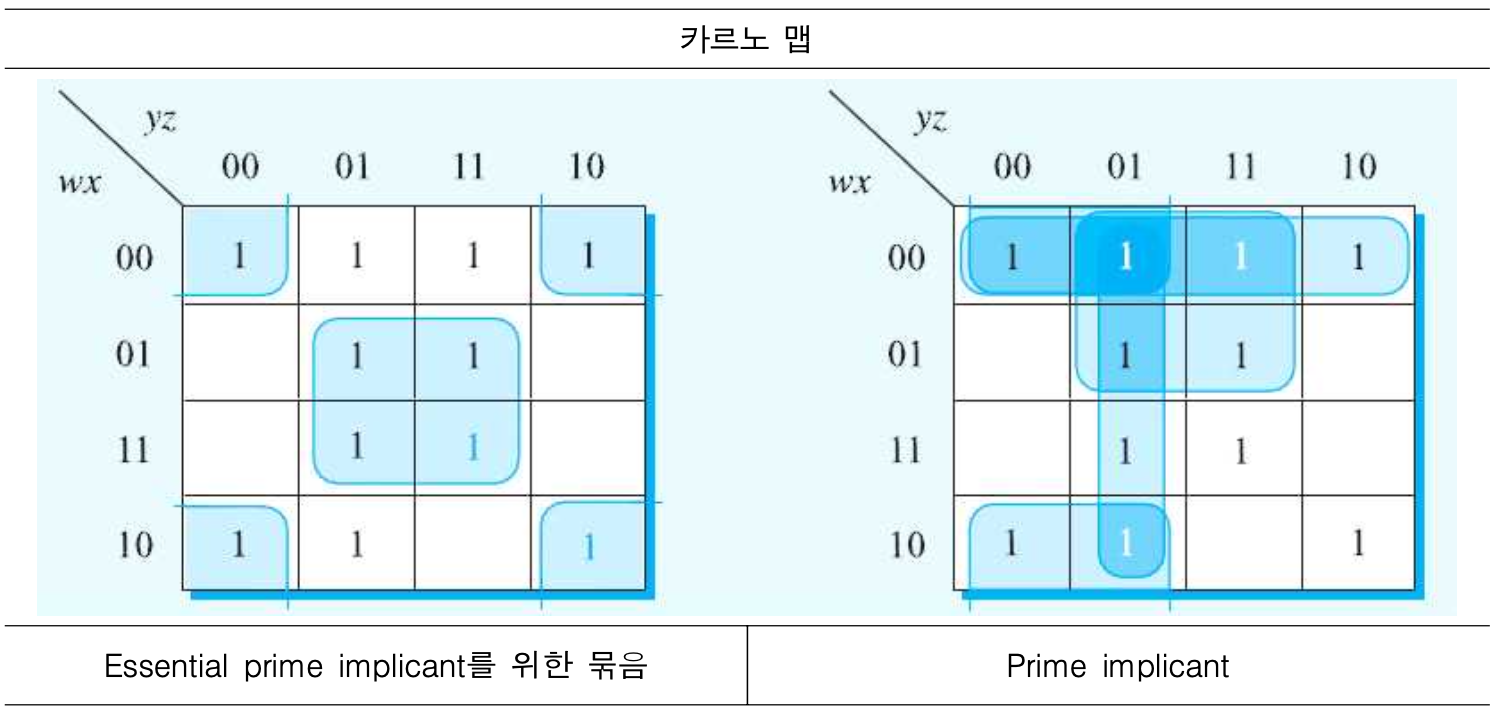
• Essential prime implicants : x’z’, xz
• Prime implicants : w’x’, w’z, x’y’, y’z
• 간략화된 부울 함수들 : EPI는 반드시 포함, PI는 중복된 둘 중의 하나씩만 포함

  F = x'z' + xz + w'x' + x'y'
    = x'z' + xz + w'x' + y'z
    = x'z' + xz + w'z + x'y'
    = x'z' + xz + w'z + y'z

4) 예제 2

• 다음 부울 표현에 대한 카르노맵으로부터 Essential prime implicant에 해당하는 항들과
  Prime implicant에 해당하는 항들을 구하고, 그들을 이용하여 얻을 수 있는 간략화 된 부울
  함수들을 모두 나열해 보자

  예) F(w,x,y,z) = ∑(0,2,4,5,6,7,8,10,13,15)

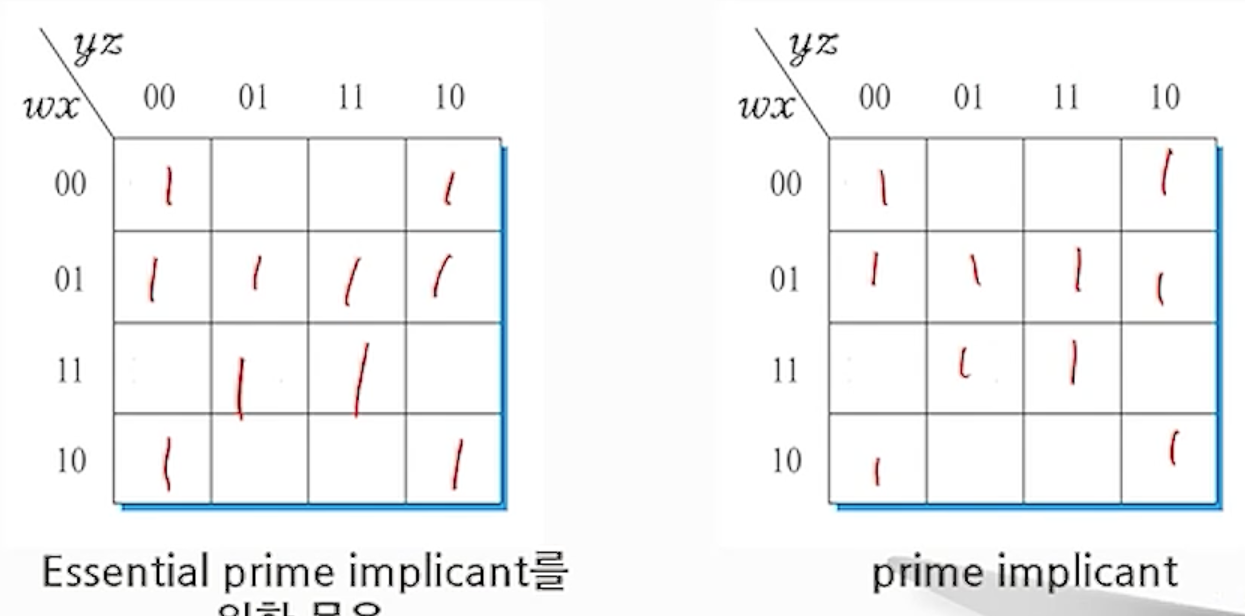
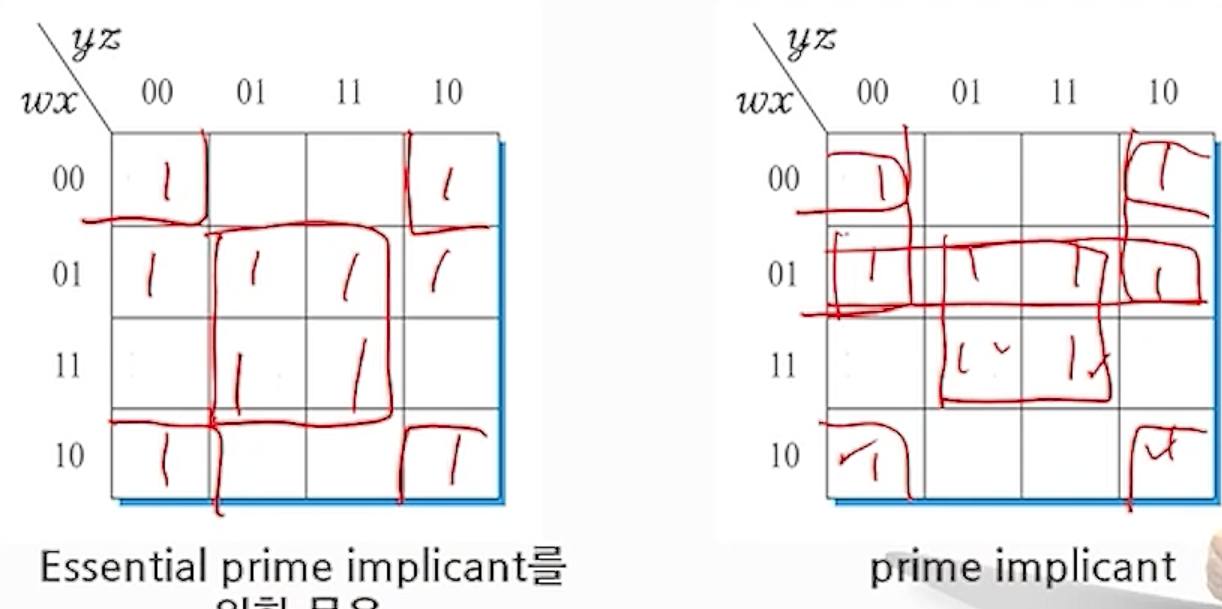
• Essential prime implicants : x’z’, xz
• Prime implicants : w’x, w’z,’
• 간략화된 부울 함수들 : (EPI는 반드시 포함, PI는 중복된 둘 중의 하나씩 만포함)

  F = x'z' + xz + w'x'
    = x'z' + xz + w'z'